Lexicographically Smallest Topological Ordering

Given a directed graph with N vertices and M edges that may contain cycles, the task is to find the lexicographically smallest topological ordering of the graph if it exists otherwise print -1 (if the graph has cycles). 
Lexicographically smallest topological ordering means that if two vertices in a graph do not have any incoming edge then the vertex with the smaller number should appear first in the ordering. 
For Example, in the image below many topological orderings are possible e.g 5 2 3 4 0 1, 5 0 2 4 3 1. 
But the smallest ordering is 4 5 0 2 3 1.

Examples:

Input:

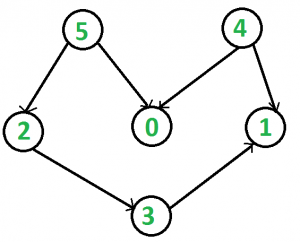
Output: 4 5 0 2 3 1 
Even though 5 4 0 2 3 1 is also a valid topological 
ordering of the given graph but it is not 
lexicographically smallest. 

Approach: We will use Kahn’s algorithm for Topological Sorting with a modification. Instead of using a queue we will use a priority queue to store the vertices to make sure that every time we pick a vertex it is the smallest possible of all. The overall Time complexity changes to 
Below is the implementation of the above approach:

CPP

// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;

vector<vector<int> > adj;

// function to add edge to the graph
void addEdge(int x, int y) { adj[x].push_back(y); }

// Function to print the required topological
// sort of the given graph
void topologicalSort()
{
    int V = adj.size();
    // Create a vector to store indegrees of all
    // the vertices
    // Initialize all indegrees to 0
    vector<int> in_degree(V, 0);

    // Traverse adjacency lists to fill indegrees of
    // vertices
    // This step takes O(V+E) time
    for (int u = 0; u < V; u++) {
        for (auto x : adj[u])
            in_degree[x]++;
    }

    // Create a min-heap priority queue and inserting all
    // vertices with indegree 0
    priority_queue<int, vector<int>, greater<int> > pq;
    for (int i = 0; i < V; i++)
        if (in_degree[i] == 0)
            pq.push(i);

    // Initialize count of visited vertices
    int cnt = 0;

    // Create a vector to store result (A topological
    // ordering of the vertices)
    vector<int> top_order;

    // One by one erase vertices from setand insert
    // adjacents if indegree of adjacent becomes 0
    while (!pq.empty()) {

        // Extract vertex with minimum number from priority
        // queue and add it to topological order
        int u = pq.top();
        pq.pop();
        top_order.push_back(u);

        // Iterate through all its neighbouring nodes
        // of erased node u and decrease their in-degree
        // by 1
        for (auto x : adj[u])

            // If in-degree becomes zero, add it to queue
            if (--in_degree[x] == 0)
                pq.push(x);

        cnt++;
    }

    // Check if there was a cycle
    if (cnt != V) {
        cout << -1;
        return;
    }

    // Print topological order
    for (int i = 0; i < top_order.size(); i++)
        cout << top_order[i] << " ";
}
int main()
{
    // number of vertices
    int v = 6;

    // adjacency matrix
    adj = vector<vector<int> >(v);

    addEdge(5, 2);
    addEdge(5, 0);
    addEdge(4, 0);
    addEdge(4, 1);
    addEdge(2, 3);
    addEdge(3, 1);

    // find required topological order
    topologicalSort();
}

Java

// Java implementation of the approach
import java.util.*;

class Main
{
  static List<List<Integer>> adj;
  
  // function to add edge to the graph
  static void addEdge(int x,int y)
  {
    adj.get(x).add(y);
  }

  // Function to print the required topological
  // sort of the given graph
  static void topologicalSort()
  {
    int V = adj.size();
    
    // Create a vector to store indegrees of all
    // the vertices
    // Initialize all indegrees to 0
    int[] in_degree = new int[V];
    Arrays.fill(in_degree, 0);

    // Traverse adjacency lists to fill indegrees of
    // vertices
    // This step takes O(V+E) time
    for (int u = 0; u < V; u++) {
      for (int x: adj.get(u))
        in_degree[x]++;
    }

    // Create a queue and inserting all vertices with
    // indegree 0
    PriorityQueue<Integer> queue = new PriorityQueue<>();
    for (int i = 0; i < V; i++)
      if (in_degree[i] == 0)
        queue.add(i);

    // Initialize count of visited vertices
    int cnt = 0;

    // Create a vector to store result (A topological
    // ordering of the vertices)
    List<Integer> top_order = new ArrayList<>();

    // One by one erase vertices from queue and insert
    // adjacents if indegree of adjacent becomes 0
    while (!queue.isEmpty()) {

      // Extract vertex with minimum number from queue
      // and add it to topological order
      int u = queue.poll();
      top_order.add(u);

      // Iterate through all its neighbouring nodes
      // of erased node u and decrease their in-degree
      // by 1
      for (int x: adj.get(u))

        // If in-degree becomes zero, add it to queue
        if (--in_degree[x] == 0)
          queue.add(x);

      cnt++;
    }

    // Check if there was a cycle
    if (cnt != V) {
      System.out.println(-1);
      return;
    }

    // Print topological order
    for (int i = 0; i < top_order.size(); i++)
      System.out.print(top_order.get(i) + " ");
  }
  public static void main (String[] args)
  {
    // number of vertices
    int v = 6;


    // adjacency matrix
    adj = new ArrayList<>(v);
    for (int i = 0; i < v; i++) {
      adj.add(new ArrayList<>());
    }

    addEdge(5,2);
    addEdge(5,0);
    addEdge(4,0);
    addEdge(4,1);
    addEdge(2,3);
    addEdge(3,1);

    // find required topological order
    topologicalSort();
  }
}

// This code is contributed by lokeshpotta20.

Python3

# Python3 implementation of the approach
import heapq as hq



# function to add edge to the graph
def addEdge(x, y):
    adj[x].append(y)


# Function to print required topological
# sort of the given graph
def topologicalSort():
    V = len(adj)
    # Create a vector to store indegrees of all
    # the vertices
    # Initialize all indegrees to 0
    in_degree = [0] * V

    # Traverse adjacency lists to fill indegrees of
    # vertices
    # This step takes O(V+E) time
    for u in range(V):
        for x in adj[u]:
            in_degree[x] += 1
    # Create a heap and inserting all vertices with
    # indegree 0
    s = []
    for i in range(V):
        if in_degree[i] == 0:
            hq.heappush(s, i)

    # Initialize count of visited vertices
    cnt = 0

    # Create a vector to store result (A topological
    # ordering of the vertices)
    top_order = []

    # One by one erase vertices from setand insert
    # adjacents if indegree of adjacent becomes 0
    while s:

        # Extract vertex with minimum number from multiset
        # and add it to topological order
        u = hq.heappop(s)
        top_order.append(u)

        # Iterate through all its neighbouring nodes
        # of erased node u and decrease their in-degree
        # by 1
        for x in adj[u]:
            in_degree[x] -= 1
            # If in-degree becomes zero, add it to queue
            if in_degree[x] == 0:
                hq.heappush(s, x)

        cnt += 1

    # Check if there was a cycle
    if cnt != V:
        print(-1)
        return

    # Print topological order
    for i in range(len(top_order)):
        print(top_order[i], end=" ")


if __name__ == "__main__":
    # number of vertices
    v = 6

    # adjacency matrix
    adj = [[] for _ in range(v)]

    addEdge(5, 2)
    addEdge(5, 0)
    addEdge(4, 0)
    addEdge(4, 1)
    addEdge(2, 3)
    addEdge(3, 1)

    # find required topological order
    topologicalSort()

JavaScript

class PriorityQueue {
  constructor() {
    this.queue = [];
  }

  add(element) {
    this.queue.push(element);
    this.queue.sort((a, b) => a - b);
  }

  poll() {
    return this.queue.shift();
  }

  isEmpty() {
    return this.queue.length === 0;
  }
}

class Main {
  constructor() {
    this.adj = [];
  }

  // function to add edge to the graph
  addEdge(x, y) {
    this.adj[x].push(y);
  }

  // Function to print the required topological
  // sort of the given graph
  topologicalSort() {
    const V = this.adj.length;

    // Create an array to store indegrees of all
    // the vertices
    // Initialize all indegrees to 0
    const in_degree = new Array(V).fill(0);

    // Traverse adjacency lists to fill indegrees of
    // vertices
    // This step takes O(V+E) time
    for (let u = 0; u < V; u++) {
      for (let x of this.adj[u])
        in_degree[x]++;
    }

    // Create a priority queue and inserting all vertices with
    // indegree 0
    const queue = new PriorityQueue();
    for (let i = 0; i < V; i++)
      if (in_degree[i] == 0)
        queue.add(i);

    // Initialize count of visited vertices
    let cnt = 0;

    // Create an array to store result (A topological
    // ordering of the vertices)
    const top_order = [];

    // One by one erase vertices from queue and insert
    // adjacents if indegree of adjacent becomes 0
    while (!queue.isEmpty()) {

      // Extract vertex with minimum number from queue
      // and add it to topological order
      let u = queue.poll();
      top_order.push(u);

      // Iterate through all its neighbouring nodes
      // of erased node u and decrease their in-degree
      // by 1
      for (let x of this.adj[u])

        // If in-degree becomes zero, add it to queue
        if (--in_degree[x] == 0)
          queue.add(x);

      cnt++;
    }

    // Check if there was a cycle
    if (cnt != V) {
      console.log(-1);
      return;
    }

    // Print topological order
    console.log(top_order.join(" "));
  }
}

// Main function
(function () {
  // number of vertices
  const v = 6;

  const main = new Main();

  // adjacency matrix
  for (let i = 0; i < v; i++) {
    main.adj.push([]);
  }

  main.addEdge(5, 2);
  main.addEdge(5, 0);
  main.addEdge(4, 0);
  main.addEdge(4, 1);
  main.addEdge(2, 3);
  main.addEdge(3, 1);

  // find required topological order
  main.topologicalSort();
})();

Output

4 5 0 2 3 1

Time Complexity: O(N)
Auxiliary Space: O(N)