Levene’s Test in R Programming
Last Updated :
16 Mar, 2023
Levene’s test is an inferential statistic used to check if the variances of a variable obtained for two or more groups are equal or not when data comes from a non-normal distribution.
Levene’s test is used to check the assumptions that the variances of the populations from different samples drawn are equal or not before running the test like ANOVA. It tests the null hypothesis that the population variances are equal or not, It is known as homoscedasticity. It’s an alternative to Bartlett’s test that is less sensitive to departures from normality.
There are several solutions to test for the homogeneity of variance (or homoscedasticity) across groups of samples are as follows:
It is very much easy to perform these tests in R programming. In this article let’s perform Levene’s test in R.
Statistical Hypotheses for Levene’s test
A hypothesis is a statement about a given problem. Hypothesis testing is a statistical method that is used in making a statistical decision using experimental data. Hypothesis testing is basically an assumption that we make about a population parameter. It evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data. To know more about the statistical hypothesis please refer to Understanding Hypothesis Testing. For Levene’s test, the statistical hypotheses are:
Null Hypothesis: All populations variances are equal
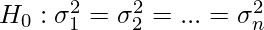
Alternative Hypothesis: At least two of them differ
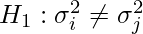
The test statistics for Levene’s test are:
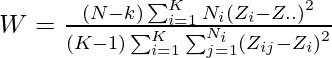
Levene’s Test in R
R provides a function leveneTest() which is available in the car package that can be used to compute Levene’s test. The syntax for this function is given below:
Syntax: leveneTest(formula, dataset)
Parameters:
formula: a formula of the form values ~ groups
dataset: a matrix or data frame
Example of Lavene’s test
Levene’s test with one independent variable:
Consider the R’s inbuilt PlantGrowth dataset that gives the dried weight of three groups of ten batches of plants, wherever every group of ten batches got a different treatment. The weight variable gives the weight of the batch and the group variable gives the treatment received either ctrl, trt1, or trt2. To view the random 5 rows of the PlantGrowth dataset use the sample_n() function from the dplyr library.
R
library("dplyr")
print(sample_n(PlantGrowth,5))
|
Output:
weight group
1 3.59 trt1
2 4.17 trt1
3 4.50 ctrl
4 5.14 ctrl
5 4.92 trt2
As mentioned above, Levene’s test is an alternative to Bartlett’s test when the data is not normally distributed. So, we consider the null and alternate hypotheses.
- The Null hypothesis is variances across all samples are equal.
- The alternative hypothesis is at least one sample has a different variance.
- We will test the null hypothesis at 0.05 significance level i.e 95% percentile.
Here let’s consider only one independent variable. To perform the test, use the below command:
R
library(car)
result = leveneTest(weight ~ group, PlantGrowth)
print(result)
|
Output:
Levene's Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 2 1.1192 0.3412
27
From the above result, we can observe that p-value = 0.34 which is greater than our significance level of 0.05. So, we do have not enough evidence to reject the null hypothesis. So the variance across the samples is equal at 0.05 significance level.
| Df
| F value
| Pr(>F)
|
| <int>
| <dbl>
| <dbl>
|
group
| 2
| 1.119186
| 0.3412266
|
| 27
| NA
| NA
|
Levene’s test with multiple independent variables:
Let’s consider the R’s inbuilt ToothGrowth dataset
R
library("dplyr")
print(sample_n(ToothGrowth,5))
|
Output:
len supp dose
1 23.6 VC 2
2 15.5 VC 1
3 16.5 VC 1
4 23.0 OJ 2
5 17.3 VC 1
If one wants to do the test with multiple independent variables then the interaction() function must be used to collapse multiple factors into a single variable containing all combinations of the factors. Here let’s take the R’s inbuilt ToothGrowth data set.
R
library(car)
result = leveneTest(len ~ interaction(supp, dose),
data = ToothGrowth)
print(result)
|
Output:
Levene's Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 5 1.7086 0.1484
54
From the above result, we can observe that p-value = 0.14 which is greater than our significance level of 0.05. So, we do have not enough evidence to reject the null hypothesis. So the variance across the samples is equal at 0.05 significance level.
| Df
| F value
| Pr(>F)
|
| <int>
| <dbl>
| <dbl>
|
group
| 5
| 1.708578
| 0.1483606
|
| 54
| NA
| NA
|
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...