Level order traversal line by line | Set 3 (Using One Queue)
Last Updated :
21 Dec, 2022
Given a Binary Tree, print the nodes level-wise, each level on a new line.
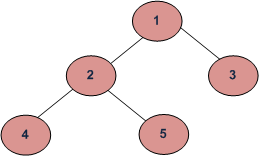
Output:
1
2 3
4 5
We have discussed two solutions in the articles below.
Print level order traversal line by line | Set 1
Level order traversal line by line | Set 2 (Using Two Queues)
In this post, a different approach using one queue is discussed. First insert the root and a null element into the queue. This null element acts as a delimiter. Next, pop from the top of the queue and add its left and right nodes to the end of the queue and then print at the top of the queue. Continue this process till the queues become empty.
C++
#include <bits/stdc++.h>
using namespace std;
struct node
{
struct node *left;
int data;
struct node *right;
};
void levelOrder(node *root)
{
if (root == NULL) return;
queue<node *> q;
node *curr;
q.push(root);
q.push(NULL);
while (q.size() > 1)
{
curr = q.front();
q.pop();
if (curr == NULL)
{
q.push(NULL);
cout << "\n";
}
else {
if(curr->left)
q.push(curr->left);
if(curr->right)
q.push(curr->right);
cout << curr->data << " ";
}
}
}
node* newNode(int data)
{
node *temp = new node;
temp->data = data;
temp->left = NULL;
temp->right = NULL;
return temp;
}
int main()
{
node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->right = newNode(6);
levelOrder(root);
return 0;
}
|
Java
import java.util.LinkedList;
import java.util.Queue;
public class GFG {
static class Node {
int data;
Node left;
Node right;
Node(int data) {
this.data = data;
left = null;
right = null;
}
}
static void levelOrder(Node root) {
if (root == null)
return;
Queue<Node> q = new LinkedList<>();
q.add(root);
q.add(null);
while (!q.isEmpty()) {
Node curr = q.poll();
if (curr == null) {
if (!q.isEmpty()) {
q.add(null);
System.out.println();
}
} else {
if (curr.left != null)
q.add(curr.left);
if (curr.right != null)
q.add(curr.right);
System.out.print(curr.data + " ");
}
}
}
public static void main(String[] args) {
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.right = new Node(6);
levelOrder(root);
}
}
|
Python3
from collections import deque as queue
class Node:
def __init__(self, key):
self.data = key
self.left = None
self.right = None
def levelOrder(root):
if (root == None):
return
q = queue()
q.append(root)
q.append(None)
while (len(q) > 1):
curr = q.popleft()
if (curr == None):
q.append(None)
print()
else:
if (curr.left):
q.append(curr.left)
if (curr.right):
q.append(curr.right)
print(curr.data, end=" ")
if __name__ == '__main__':
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.right = Node(6)
levelOrder(root)
|
C#
using System;
using System.Collections;
class GFG
{
public class Node
{
public int data;
public Node left;
public Node right;
public Node(int data)
{
this.data = data;
left = null;
right = null;
}
}
static void levelOrder(Node root)
{
if (root == null)
return;
Queue q = new Queue();
q.Enqueue(root);
q.Enqueue(null);
while (q.Count>0)
{
Node curr = (Node)q.Peek();
q.Dequeue();
if (curr == null)
{
if (q.Count > 0)
{
q.Enqueue(null);
Console.WriteLine();
}
}
else
{
if (curr.left != null)
q.Enqueue(curr.left);
if (curr.right != null)
q.Enqueue(curr.right);
Console.Write(curr.data + " ");
}
}
}
static public void Main(String []args)
{
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.right = new Node(6);
levelOrder(root);
}
}
|
Javascript
<script>
class Node
{
constructor(data)
{
this.data = data;
this.left = null;
this.right = null;
}
}
function levelOrder(root)
{
if (root == null)
return;
let q= [];
q.push(root);
q.push(null);
while (q.length!=0) {
let curr = q.shift();
if (curr == null) {
if (q.length!=0) {
q.push(null);
document.write("<br>");
}
}
else {
if (curr.left != null)
q.push(curr.left);
if (curr.right != null)
q.push(curr.right);
document.write(curr.data + " ");
}
}
}
let root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.right = new Node(6);
levelOrder(root);
</script>
|
Time Complexity: O(n)
Auxiliary Space: O(n) for queue, where n is no of nodes of binary tree
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...