Level order traversal in spiral form
Last Updated :
09 Aug, 2023
Given a Binary Tree, the task is to print the Level order traversal of the Binary Tree in spiral form i.e, alternate order.
Example:
Input:
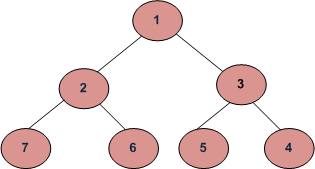
Output: 1 2 3 4 5 6 7
Explanation:
Level 1: 1
Level 2: 2 3
Level 3: 7 6 5 4
Nodes are traversed in the alternate order from front or back in adjacent levels , so the output is 1 2 3 4 5 6 7.
The idea is to first calculate the height of the tree, then recursively traverse each level and print the level order traversal according to the current level.
Follow the below steps to Implement the idea:
- Initialize a variable h to store the height of the binary tree.
- Initialize a variable i, and ltr = false.
- Traverse a loop from 1 till h:
- Print the level order traversal of given traversal using below recursive function:
- printGivenLevel(tree, level, ltr)
- if tree is NULL then return;
- if level is 1, then
- else if level greater than 1, then
- if(ltr)
- printGivenLevel(tree->left, level-1, ltr);
- printGivenLevel(tree->right, level-1, ltr);
- else
- printGivenLevel(tree->right, level-1, ltr);
- printGivenLevel(tree->left, level-1, ltr);
- Update ltr = !ltr
Following is the implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
struct node {
int data;
struct node* left;
struct node* right;
};
void printGivenLevel(struct node* root, int level, int ltr);
int height(struct node* node);
struct node* newNode(int data);
void printSpiral(struct node* root)
{
int h = height(root);
int i;
bool ltr = false;
for (i = 1; i <= h; i++) {
printGivenLevel(root, i, ltr);
ltr = !ltr;
}
}
void printGivenLevel(struct node* root, int level, int ltr)
{
if (root == NULL)
return;
if (level == 1)
cout << root->data << " ";
else if (level > 1) {
if (ltr) {
printGivenLevel(root->left, level - 1, ltr);
printGivenLevel(root->right, level - 1, ltr);
}
else {
printGivenLevel(root->right, level - 1, ltr);
printGivenLevel(root->left, level - 1, ltr);
}
}
}
int height(struct node* node)
{
if (node == NULL)
return 0;
else {
int lheight = height(node->left);
int rheight = height(node->right);
if (lheight > rheight)
return (lheight + 1);
else
return (rheight + 1);
}
}
struct node* newNode(int data)
{
node* newnode = new node();
newnode->data = data;
newnode->left = NULL;
newnode->right = NULL;
return (newnode);
}
int main()
{
struct node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(7);
root->left->right = newNode(6);
root->right->left = newNode(5);
root->right->right = newNode(4);
printf("Spiral Order traversal of "
"binary tree is \n");
printSpiral(root);
return 0;
}
|
C
#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node* left;
struct node* right;
};
void printGivenLevel(struct node* root, int level, int ltr);
int height(struct node* node);
struct node* newNode(int data);
void printSpiral(struct node* root)
{
int h = height(root);
int i;
bool ltr = false;
for (i = 1; i <= h; i++) {
printGivenLevel(root, i, ltr);
ltr = !ltr;
}
}
void printGivenLevel(struct node* root, int level, int ltr)
{
if (root == NULL)
return;
if (level == 1)
printf("%d ", root->data);
else if (level > 1) {
if (ltr) {
printGivenLevel(root->left, level - 1, ltr);
printGivenLevel(root->right, level - 1, ltr);
}
else {
printGivenLevel(root->right, level - 1, ltr);
printGivenLevel(root->left, level - 1, ltr);
}
}
}
int height(struct node* node)
{
if (node == NULL)
return 0;
else {
int lheight = height(node->left);
int rheight = height(node->right);
if (lheight > rheight)
return (lheight + 1);
else
return (rheight + 1);
}
}
struct node* newNode(int data)
{
struct node* node
= (struct node*)malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
int main()
{
struct node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(7);
root->left->right = newNode(6);
root->right->left = newNode(5);
root->right->right = newNode(4);
printf("Spiral Order traversal of binary tree is \n");
printSpiral(root);
return 0;
}
|
Java
class Node {
int data;
Node left, right;
public Node(int d)
{
data = d;
left = right = null;
}
}
class BinaryTree {
Node root;
void printSpiral(Node node)
{
int h = height(node);
int i;
boolean ltr = false;
for (i = 1; i <= h; i++) {
printGivenLevel(node, i, ltr);
ltr = !ltr;
}
}
int height(Node node)
{
if (node == null)
return 0;
else {
int lheight = height(node.left);
int rheight = height(node.right);
if (lheight > rheight)
return (lheight + 1);
else
return (rheight + 1);
}
}
void printGivenLevel(Node node, int level, boolean ltr)
{
if (node == null)
return;
if (level == 1)
System.out.print(node.data + " ");
else if (level > 1) {
if (ltr != false) {
printGivenLevel(node.left, level - 1, ltr);
printGivenLevel(node.right, level - 1, ltr);
}
else {
printGivenLevel(node.right, level - 1, ltr);
printGivenLevel(node.left, level - 1, ltr);
}
}
}
public static void main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(7);
tree.root.left.right = new Node(6);
tree.root.right.left = new Node(5);
tree.root.right.right = new Node(4);
System.out.println(
"Spiral order traversal of Binary Tree is ");
tree.printSpiral(tree.root);
}
}
|
Python3
class newNode:
def __init__(self, key):
self.data = key
self.left = None
self.right = None
def printSpiral(root):
h = height(root)
ltr = False
for i in range(1, h + 1):
printGivenLevel(root, i, ltr)
ltr = not ltr
def printGivenLevel(root, level, ltr):
if(root == None):
return
if(level == 1):
print(root.data, end=" ")
elif (level > 1):
if(ltr):
printGivenLevel(root.left, level - 1, ltr)
printGivenLevel(root.right, level - 1, ltr)
else:
printGivenLevel(root.right, level - 1, ltr)
printGivenLevel(root.left, level - 1, ltr)
def height(node):
if (node == None):
return 0
else:
lheight = height(node.left)
rheight = height(node.right)
if (lheight > rheight):
return(lheight + 1)
else:
return(rheight + 1)
if __name__ == '__main__':
root = newNode(1)
root.left = newNode(2)
root.right = newNode(3)
root.left.left = newNode(7)
root.left.right = newNode(6)
root.right.left = newNode(5)
root.right.right = newNode(4)
print("Spiral Order traversal of binary tree is")
printSpiral(root)
|
C#
using System;
public class Node {
public int data;
public Node left, right;
public Node(int d)
{
data = d;
left = right = null;
}
}
class GFG {
public Node root;
public virtual void printSpiral(Node node)
{
int h = height(node);
int i;
bool ltr = false;
for (i = 1; i <= h; i++) {
printGivenLevel(node, i, ltr);
ltr = !ltr;
}
}
public virtual int height(Node node)
{
if (node == null) {
return 0;
}
else {
int lheight = height(node.left);
int rheight = height(node.right);
if (lheight > rheight) {
return (lheight + 1);
}
else {
return (rheight + 1);
}
}
}
public virtual void printGivenLevel(Node node,
int level, bool ltr)
{
if (node == null) {
return;
}
if (level == 1) {
Console.Write(node.data + " ");
}
else if (level > 1) {
if (ltr != false) {
printGivenLevel(node.left, level - 1, ltr);
printGivenLevel(node.right, level - 1, ltr);
}
else {
printGivenLevel(node.right, level - 1, ltr);
printGivenLevel(node.left, level - 1, ltr);
}
}
}
public static void Main(string[] args)
{
GFG tree = new GFG();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(7);
tree.root.left.right = new Node(6);
tree.root.right.left = new Node(5);
tree.root.right.right = new Node(4);
Console.WriteLine("Spiral order traversal "
+ "of Binary Tree is ");
tree.printSpiral(tree.root);
}
}
|
Javascript
<script>
class Node
{
constructor(d) {
this.left = null;
this.right = null;
this.data = d;
}
}
let root;
function printSpiral(node)
{
let h = height(node);
let i;
let ltr = false;
for (i = 1; i <= h; i++) {
printGivenLevel(node, i, ltr);
ltr = !ltr;
}
}
function height(node)
{
if (node == null)
return 0;
else {
let lheight = height(node.left);
let rheight = height(node.right);
if (lheight > rheight)
return (lheight + 1);
else
return (rheight + 1);
}
}
function printGivenLevel(node, level, ltr)
{
if (node == null)
return;
if (level == 1)
document.write(node.data + " ");
else if (level > 1) {
if (ltr != false) {
printGivenLevel(node.left, level - 1, ltr);
printGivenLevel(node.right, level - 1, ltr);
}
else {
printGivenLevel(node.right, level - 1, ltr);
printGivenLevel(node.left, level - 1, ltr);
}
}
}
root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(7);
root.left.right = new Node(6);
root.right.left = new Node(5);
root.right.right = new Node(4);
document.write("Spiral order traversal of Binary Tree is " +
"</br>");
printSpiral(root);
</script>
|
Output
Spiral Order traversal of binary tree is
1 2 3 4 5 6 7
Time Complexity: O(N2), where N is the number of nodes in the given tree.
Auxiliary Space: O(N), for recursive stack space.
The idea is to use two separate stacks to store the level order traversal as per their levels in adjacent order.
Follow the below steps to Implement the idea:
- Initialize two stacks s1 and s2
- Push the root of tree in s1
- Initialize a while loop till either s1 or s2 is non-empty
- Initialize a nested while loop till s1 contains nodes
- Initialize temp = s1.top()
- Pop the node from s1
- Print temp -> data
- If temp -> right is not NULL
- Insert temp -> right in s2
- If temp -> left is not NULL
- Insert temp -> left in s2
- Initialize a nested while loop till s2 contains nodes
- Initialize temp = s2.top()
- Pop the node from s2
- Print temp -> data
- If temp -> left is not NULL
- Insert temp -> left in s1
- If temp -> right is not NULL
- Insert temp -> right in s1
Below is the implementation of the above approach:
C++
#include <iostream>
#include <stack>
using namespace std;
struct node {
int data;
struct node *left, *right;
};
void printSpiral(struct node* root)
{
if (root == NULL)
return;
stack<struct node*>
s1;
stack<struct node*>
s2;
s1.push(root);
while (!s1.empty() || !s2.empty()) {
while (!s1.empty()) {
struct node* temp = s1.top();
s1.pop();
cout << temp->data << " ";
if (temp->right)
s2.push(temp->right);
if (temp->left)
s2.push(temp->left);
}
while (!s2.empty()) {
struct node* temp = s2.top();
s2.pop();
cout << temp->data << " ";
if (temp->left)
s1.push(temp->left);
if (temp->right)
s1.push(temp->right);
}
}
}
struct node* newNode(int data)
{
struct node* node = new struct node;
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
int main()
{
struct node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(7);
root->left->right = newNode(6);
root->right->left = newNode(5);
root->right->right = newNode(4);
cout << "Spiral Order traversal of binary tree is \n";
printSpiral(root);
return 0;
}
|
Java
import java.util.*;
class Node {
int data;
Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
class BinaryTree {
static Node root;
void printSpiral(Node node)
{
if (node == null)
return;
Stack<Node> s1 = new Stack<Node>();
Stack<Node> s2 = new Stack<Node>();
s1.push(node);
while (!s1.empty() || !s2.empty()) {
while (!s1.empty()) {
Node temp = s1.peek();
s1.pop();
System.out.print(temp.data + " ");
if (temp.right != null)
s2.push(temp.right);
if (temp.left != null)
s2.push(temp.left);
}
while (!s2.empty()) {
Node temp = s2.peek();
s2.pop();
System.out.print(temp.data + " ");
if (temp.left != null)
s1.push(temp.left);
if (temp.right != null)
s1.push(temp.right);
}
}
}
public static void main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(7);
tree.root.left.right = new Node(6);
tree.root.right.left = new Node(5);
tree.root.right.right = new Node(4);
System.out.println(
"Spiral Order traversal of Binary Tree is ");
tree.printSpiral(root);
}
}
|
Python3
class newNode:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def printSpiral(root):
if (root == None):
return
s1 = []
s2 = []
s1.append(root)
while not len(s1) == 0 or not len(s2) == 0:
while not len(s1) == 0:
temp = s1[-1]
s1.pop()
print(temp.data, end=" ")
if (temp.right):
s2.append(temp.right)
if (temp.left):
s2.append(temp.left)
while (not len(s2) == 0):
temp = s2[-1]
s2.pop()
print(temp.data, end=" ")
if (temp.left):
s1.append(temp.left)
if (temp.right):
s1.append(temp.right)
if __name__ == '__main__':
root = newNode(1)
root.left = newNode(2)
root.right = newNode(3)
root.left.left = newNode(7)
root.left.right = newNode(6)
root.right.left = newNode(5)
root.right.right = newNode(4)
print("Spiral Order traversal of",
"binary tree is ")
printSpiral(root)
|
C#
using System;
using System.Collections.Generic;
public class Node {
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
public class BinaryTree {
public static Node root;
public virtual void printSpiral(Node node)
{
if (node == null) {
return;
}
Stack<Node> s1
= new Stack<Node>();
Stack<Node> s2
= new Stack<Node>();
s1.Push(node);
while (s1.Count > 0 || s2.Count > 0) {
while (s1.Count > 0) {
Node temp = s1.Peek();
s1.Pop();
Console.Write(temp.data + " ");
if (temp.right != null) {
s2.Push(temp.right);
}
if (temp.left != null) {
s2.Push(temp.left);
}
}
while (s2.Count > 0) {
Node temp = s2.Peek();
s2.Pop();
Console.Write(temp.data + " ");
if (temp.left != null) {
s1.Push(temp.left);
}
if (temp.right != null) {
s1.Push(temp.right);
}
}
}
}
public static void Main(string[] args)
{
BinaryTree tree = new BinaryTree();
BinaryTree.root = new Node(1);
BinaryTree.root.left = new Node(2);
BinaryTree.root.right = new Node(3);
BinaryTree.root.left.left = new Node(7);
BinaryTree.root.left.right = new Node(6);
BinaryTree.root.right.left = new Node(5);
BinaryTree.root.right.right = new Node(4);
Console.WriteLine(
"Spiral Order traversal of Binary Tree is ");
tree.printSpiral(root);
}
}
|
Javascript
<script>
class Node
{
constructor(item) {
this.left = null;
this.right = null;
this.data = item;
}
}
let root;
function printSpiral(node)
{
if (node == null) {
return;
}
let s1 = [];
let s2 = [];
s1.push(node);
while (s1.length > 0 || s2.length > 0) {
while (s1.length > 0) {
let temp = s1[s1.length - 1];
s1.pop();
document.write(temp.data + " ");
if (temp.right != null) {
s2.push(temp.right);
}
if (temp.left != null) {
s2.push(temp.left);
}
}
while (s2.length > 0) {
let temp = s2[s2.length - 1];
s2.pop();
document.write(temp.data + " ");
if (temp.left != null) {
s1.push(temp.left);
}
if (temp.right != null) {
s1.push(temp.right);
}
}
}
}
root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(7);
root.left.right = new Node(6);
root.right.left = new Node(5);
root.right.right = new Node(4);
document.write("Spiral Order traversal of Binary Tree is " + "</br>");
printSpiral(root);
</script>
|
Output
Spiral Order traversal of binary tree is
1 2 3 4 5 6 7
Time Complexity: O(N), where N is the number of nodes in the binary tree.
Auxiliary Space: O(N), for storing the nodes in the stack.
The idea is to use Doubly Ended Queues, then push and pop the nodes from each end in alternate order.
Follow the below steps to Implement the idea:
- Initialize a deque dq.
- Push root of the binary tree in dq
- Initialize a variable reverse = true
- Initialize a loop while dq is not empty:
- Initialize n = dq.size()
- IF reverse == false:
- Initialize a nested loop while n > 0:
- Decrement n by 1
- If dq.front()->left is not NULL
- Push dq.front()->left at the back of Deque
- If dq.front()->right is not NULL
- Push dq.front()->right at the back of Deque
- Print dq.front()->key
- Pop the node from front of the Deque
- Update reverse = !reverse
- Else
- Initialize a nested loop while n > 0:
- Decrement n by 1
- If dq.back()->right is not NULL
- Push dq.front()->right to the front of Deque
- If dq.back()->left is not NULL
- Push dq.front()->left to the front of Deque
- Print dq.back()->key
- Pop the node from back of the Deque
- Update reverse = !reverse
Below is the implementation of the above approach:
C++
#include <iostream>
#include <stack>
using namespace std;
struct Node {
int key;
struct Node *left, *right;
};
void spiralPrint(struct Node* root)
{
deque<Node*> dq;
dq.push_back(root);
bool reverse = true;
while (!dq.empty()) {
int n = dq.size();
if (!reverse) {
while (n--) {
if (dq.front()->left != NULL)
dq.push_back(dq.front()->left);
if (dq.front()->right != NULL)
dq.push_back(dq.front()->right);
cout << dq.front()->key << " ";
dq.pop_front();
}
reverse = !reverse;
}
else {
while (n--) {
if (dq.back()->right != NULL)
dq.push_front(dq.back()->right);
if (dq.back()->left != NULL)
dq.push_front(dq.back()->left);
cout << dq.back()->key << " ";
dq.pop_back();
}
reverse = !reverse;
}
}
}
struct Node* newNode(int data)
{
struct Node* node = new struct Node;
node->key = data;
node->left = NULL;
node->right = NULL;
return (node);
}
int main()
{
struct Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(7);
root->left->right = newNode(6);
root->right->left = newNode(5);
root->right->right = newNode(4);
cout << "Spiral Order traversal of binary tree is :\n";
spiralPrint(root);
return 0;
}
|
Java
import java.io.*;
import java.util.ArrayDeque;
import java.util.Deque;
class GFG {
static class Node {
int key;
Node left;
Node right;
public Node(int key) { this.key = key; }
}
static class MyTree {
public MyTree(){};
public Node root;
}
public static void spiralPrint(Node root)
{
Deque<Node> dq = new ArrayDeque<>();
dq.offer(root);
boolean reverse = true;
while (!dq.isEmpty()) {
int n = dq.size();
if (!reverse) {
while (n-- > 0) {
if (dq.peekFirst().left != null)
dq.offerLast(dq.peekFirst().left);
if (dq.peekFirst().right != null)
dq.offerLast(dq.peekFirst().right);
System.out.print(dq.pollFirst().key
+ " ");
}
reverse = !reverse;
}
else {
while (n-- > 0) {
if (dq.peekLast().right != null)
dq.offerFirst(dq.peekLast().right);
if (dq.peekLast().left != null)
dq.offerFirst(dq.peekLast().left);
System.out.print(dq.pollLast().key
+ " ");
}
reverse = !reverse;
}
}
}
public static void main(String[] args)
{
MyTree mt = new MyTree();
mt.root = new Node(1);
mt.root.left = new Node(2);
mt.root.right = new Node(3);
mt.root.left.left = new Node(7);
mt.root.left.right = new Node(6);
mt.root.right.left = new Node(5);
mt.root.right.right = new Node(4);
System.out.println(
"Spiral Order Traversal Of The Tree is :");
spiralPrint(mt.root);
}
}
|
Python3
from collections import deque
class newNode:
def __init__(self, data):
self.key = data
self.left = None
self.right = None
def spiralPrint(root):
dq = deque()
dq.append(root)
reverse = True
while (len(dq)):
n = len(dq)
if(not reverse):
while (n > 0):
n -= 1
if (dq[0].left != None):
dq.append(dq[0].left)
if (dq[0].right != None):
dq.append(dq[0].right)
print(dq[0].key, end=" ")
dq.popleft()
reverse = not reverse
else:
while (n > 0):
n -= 1
if (dq[-1].right != None):
dq.appendleft(dq[-1].right)
if (dq[-1].left != None):
dq.appendleft(dq[-1].left)
print(dq[-1].key, end=" ")
dq.pop()
reverse = not reverse
if __name__ == '__main__':
root = newNode(1)
root.left = newNode(2)
root.right = newNode(3)
root.left.left = newNode(7)
root.left.right = newNode(6)
root.right.left = newNode(5)
root.right.right = newNode(4)
print("Spiral Order traversal of",
"binary tree is :")
spiralPrint(root)
|
C#
using System;
using System.Collections.Generic;
public class Node {
public int key;
public Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
public class BinaryTree {
public static Node root;
public virtual void spiralPrint(Node root)
{
List<Node> dq = new List<Node>();
dq.Add(root);
bool reverse = true;
while (dq.Count != 0) {
int n = dq.Count;
if (!reverse) {
while (n-- > 0) {
if (dq[0].left != null)
dq.Add(dq[0].left);
if (dq[0].right != null)
dq.Add(dq[0].right);
Console.Write(dq[0].key + " ");
dq.RemoveAt(0);
}
reverse = !reverse;
}
else {
while (n-- > 0) {
if (dq[dq.Count - 1].right != null)
dq.Insert(0,
dq[dq.Count - 1].right);
if (dq[dq.Count - 1].left != null)
dq.Insert(0, dq[dq.Count - 1].left);
Console.Write(dq[dq.Count - 1].key
+ " ");
dq.RemoveAt(dq.Count - 1);
}
reverse = !reverse;
}
}
}
public static void Main(string[] args)
{
BinaryTree tree = new BinaryTree();
BinaryTree.root = new Node(1);
BinaryTree.root.left = new Node(2);
BinaryTree.root.right = new Node(3);
BinaryTree.root.left.left = new Node(7);
BinaryTree.root.left.right = new Node(6);
BinaryTree.root.right.left = new Node(5);
BinaryTree.root.right.right = new Node(4);
Console.WriteLine(
"Spiral Order traversal of Binary Tree is :");
tree.spiralPrint(root);
}
}
|
Javascript
class Node
{
constructor(item) {
this.left = null;
this.right = null;
this.data = item;
}
}
let root;
function printSpiral(node)
{
if (node == null) {
return;
}
let s1 = [];
let s2 = [];
s1.push(node);
while (s1.length > 0 || s2.length > 0) {
while (s1.length > 0) {
let temp = s1[s1.length - 1];
s1.pop();
document.write(temp.data + " ");
if (temp.right != null) {
s2.push(temp.right);
}
if (temp.left != null) {
s2.push(temp.left);
}
}
while (s2.length > 0) {
let temp = s2[s2.length - 1];
s2.pop();
document.write(temp.data + " ");
if (temp.left != null) {
s1.push(temp.left);
}
if (temp.right != null) {
s1.push(temp.right);
}
}
}
}
root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(7);
root.left.right = new Node(6);
root.right.left = new Node(5);
root.right.right = new Node(4);
document.write("Spiral Order traversal of Binary Tree is " + "</br>");
printSpiral(root);
|
Output
Spiral Order Traversal Of The Tree Is :
1 2 3 4 5 6 7
Time Complexity: O(N), where N is the number of nodes in the binary tree.
Auxiliary Space: O(N), for storing the nodes in the Deque.
Please write comments if you find any bug in the above program/algorithm; or if you want to share more information about spiral traversal.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...