The light is an electromagnetic, transverse, wave that can be seen or caught by the typical human eye. The wave nature of light was first illustrated through the experiments on diffraction and interference. When these light rays fall onto the lenses then lenses behave depending on the type of lens it is falling on. The light rays may be diffracted or interfered with depending on the foci of the lens. Basically, lenses are magnifying glasses with curved sides. They also have magnifying property due to which they are used in telescopes and other magnifying devices. They are also used in cameras to capture light rays.
What is a Lens?
Lenses are basically curved-sided magnifying lenses. A lens is a fragment of translucent glass that, by refraction, concentrates or disperses light rays. Lenses are used in telescopes and other magnifying instruments because of their magnifying property. They are used in cameras to collect light rays. In cameras, light is collected by a collection of lenses rather than by a single lens. A lens’s magnification is the relationship between the size of the image produced and the size of the target. Lenses may also be used in groups to reduce blurriness or distortion in the picture created by the lens.
Thus, a lens is a small piece of material that is modified to catch up with an image with the help of rays of light. In this article, we are going to discuss the lens formula, terms related to it, and also the derivation of magnification using the lens formula.
Related Terms to a Lens
- Pole: The center of the spherical surface of the lens is called the pole or The point where the principal axis meets the surface of the lens. It is represented by ‘P’.
- Principal axis: The principal axis is an imaginary line passing through the pole and center of curvature.
- Aperture: Aperture is defined as the area of the lens suitable for refraction. The aperture of the lens is the effective diameter of its light-transmitting area.
- Focus: Focus is defined as the point onto which collimated light parallel to the axis is focused.
- Focal length: The focal length is the distance between the optical center and the focal point or focus of the lens.
- Power: It is defined as the inverse of its focal length. The S.I unit of power is Dioptre.
Types of Lenses
There is a wide range of lenses in today’s usage and generally, they are categorized into two types compound lens and simple lens. And according to the shape and the purpose of the lens is classified into two types concave lens and convex lens which we are going to discuss below.
Simple lens: This simple lens has a 2x to 6x power lens that is used to magnify the letters on the newspaper. And these are simply used to magnify the objects. By using a simple lens it magnifies the object to 6 times larger than its original object. And moreover, it has a lower strength to magnify the object when compared to the other lens. The best example of a simple lens is spectacles. In addition, simple lens quality is not quite good, and they produce low-quality images.
Compound lens: The compound lens magnifies the object and projects to produce a clear image of an image. The quality of the image produced by the compound lens is good compared to the images produced by the simple lens. Mostly the compound lens is used in microscopes and telescopes. This lens produces 4x,10x, 40x,100x and 400x images, it magnifies the object to 4 times,10 times, 40 times,100 times, and 400 times larger images than the object. More than one lens focuses on the image to produce the image in a compound lens. The formula used for calculating a microscope’s magnification is given below:
MA= Mo × Me
where Mo is the magnification of the objective and Me is the magnification of the eyepiece.
Non-spherical Lenses
- Aspheric Lens: The aspheric lens is often known as a non-spherical lens. An aspheric lens is a lens whose surface is neither a part of a sphere nor a cylinder. As it has a complex surface it eliminates optical divergence as compared to a simple lens. A single aspheric lens can replace with a combination of simple lenses resulting in a system with a much-reduced size.
- Cylindrical Lens: Lenses that have a curvature along only one axis are classified as cylindrical lenses. Their main use is to convert the laser diode light which is elliptical in nature into a round beam or to focus light into a line. An example of cylindrical lenses is motion picture anamorphic lenses.
- Fresnel Lens: A Fresnel lens is a lens whose optical surface is divided into narrow rings. That allows the lens to be much thinner and lighter than conventional lenses.
Spherical Lenses: In principle, spherical lenses, like spherical mirrors, are a part cut off from a bigger sphere. The refractive index of glass is higher than that of the surrounding air. Light rays passing from air to glass are obviously refracted. In cameras, light is collected by a collection of lenses rather than by a single lens. A lens’s magnification is the relationship between the size of the image produced and the size of the target. Lenses may also be used in groups to reduce blurriness or distortion in the picture created by the lens.
Further, the spherical lenses are of two types: Concave and Convex lenses, which are discussed more in the following topics.
Concave Lens
A concave lens is a type of lens with one side curved inwards. This lens with both sides curved inward is called a biconcave lens. Concave lenses are diverging lenses, i.e, they spread light rays that have been refracted through them. They even have the ability to diverge a parallel beam of light. For a concave lens, the edges are wider than the center or the center is thinner than the edges. These are used in spectacles in order to treat myopia or short-sightedness. The concave lens is also called a diverging lens as rays of light diverge when rays of light fall on the lens. A concave lens has two focal points to the two sides and these focal points are equidistance to the curvature. It produces a smaller image for the viewer. The focal point of a concave lens is a point from which the light rays are parallel to the axis seem to diverge, after passing through the lens. The distance from the optical center of the lens to the focal point is called the focal length of the lens.
The image formed in a concave lens must have the following characteristics:
- Located on the object-side of the lens
- A virtual image is formed.
- An upright image formed.
- Small in size (image size must be smaller than the object size).
- The image formed by a concave lens is always should be in between the focal point and the optical center. The position of the object doesn’t affect the characteristics of the image formed.
Convex Lens
A convex lens is a type of lens with an outward curve. Compared to a concave lens, the thickness at the center of a convex lens is more than the thickness at the edges of the lens. The convex lenses are converging in nature. It has the ability to converge a parallel beam of light into a point. This point is called the focal point of the convex lens and the distance from the optical center to the focal point is called the focal length. The focal point is on the opposite side of the lens from which the light rays originate. A convex lens with one side flat is called a Plano-convex lens. The lens found in the human eye is a prime example of a convex lens. Another common example of a convex lens is the magnifying glass that is used to correct Hypermetropia or long-sightedness. Convex lenses are used in cameras as they focus the light and produce a clear image. Convex lenses are also used in compound lenses which are employed in magnifying devices such as microscopes and telescopes
Lens Formula Derivation
Now let us derive the lens formula with the help of the diagram shown below:
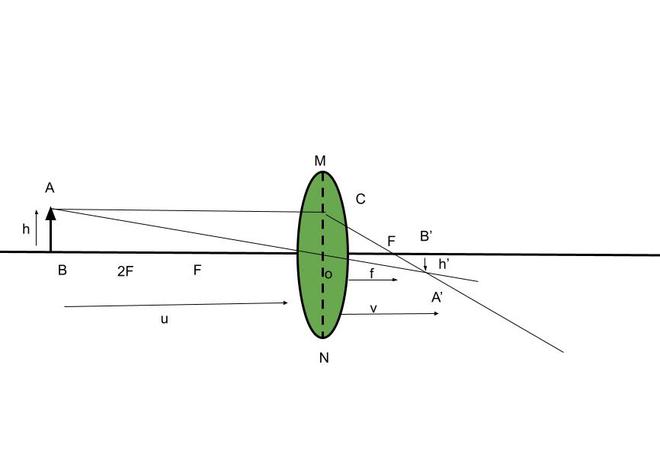
From the above figure, we can write as
A′B′/AB = OB′/OB ……(1)
Similarly, △A’B’F and △OCF are similar, therefore
A′B′/OC = FB′/OF
But, OC = AB
This implies,
A′B′/AB = FB′/OF …….(2)
By Equating equation (1) and (2), we get
OB′/OB = FB′/OF = OB′− OF/OF
By substituting the sign convention, we get
OB = -u, OB’ = v, and OF = f
−u = v − f/f
vf = −uv + uf
or
uv = uf − vf
Now divide both the sides by uvf, we get
uv/uvf = uf/uvf − vf/uvf
1/f =1/v −1/u
which is the required Lens formula.
where f is the focal length.
u is the object’s distance from the lens.
v is the image distance from the lens.
Magnification of Lens
Magnification refers to enlarging something, it means that the object itself doesn’t become physically larger but only larger in its appearance. The magnification can arise in either of two forms they are microscopic magnification and telescopic magnification. Microscopic magnification comes into the picture when we place a small object, and it appears larger. Telescopic magnification comes to the picture when larger objects appear small. And there are two types of magnification lens in usage they are a simple lens and compound lens.
The Magnification lens is given as below:
m = h’ / h = v / u
where m is the magnification, h is the height of the object, h’ is the height of the image, v is the distance of image from lens and u = distance of object from lens
Note: If m is positive then we can say that the image formed is virtual and erect and if m is negative the image formed is real and inverted.
Power of lens
The power of a lens is the measure of the degree of convergence or divergence which depends on the focal length of the lens. We define the power of the lens as the reciprocal of the focal length of the lens used. It is given by:
P = 1 / f
The SI unit of Power is Dioptre (D). The power of the concave lens is negative, while the power of the convex lens can be positive.
Sample Problem
Problem 1: What is the length of the image produced by placing the object of 10cm away from a convex lens of focal length equal to 5 cm?
Solution:
Given that,
The focal length, f is 5 cm.
As the object is on the left side so, the object distance, u is -10 cm.
Using the lens formula, the focal length is given by:
1/f = 1/v – 1/u
where v is the image distance.
1/5 cm = 1/v – 1/(-10 cm)
Now, Solve for v as:
1/v = 1/5 cm – 1/10 cm
= 1/10 cm
v = 10 cm
Therefore, the distance of the image is 10 cm.
Problem 2: In a convex lens, if the distance of the image is positive then what is the nature of the image?
Solution:
Given that, the distance of the image is positive that means the image is created on the right side of the lens.
If the image is created on the right side of the lens then the nature of the image is real and inverted.
Problem 3: If an object is placed at a distance of 3 cm from a concave lens of focal length 12 cm. Find the position and nature of the image?
Solution:
Given that,
The focal length, f is -12 cm.
The object distance of the concave lens, u is -3 cm.
By using the lens formula,
1/f = 1/v – 1/u
where v is the image distance.
1/(-12 cm) = 1/v – 1/(-3 cm)
1/v = -1/3 – 1/12
= -5/12
v = -2.4cm
Hence, the image is formed at 2.4 cm in front of the concave lens (on its left side), Virtual and erect.
Problem 4: The magnification of the mirror is -3 cm and the height of the object is 16cm then what is the length and nature of the image formed?
Solution:
Given that,
The height of the object, h is 16 cm.
The magnification, m is -3cm.
The formula to calculate the magnification is:
m = h’/h
where h’ is the height of the image.
Substitute the given values in the above expression as:
-3 cm = h’/16 cm
Solve for h’ as:
h’ = -3 × 16
= -48cm
Therefore, the height of image is 48 cm.
Since, m is negative, so the nature of the image is real and inverted.
Problem 5: What is the power of the concave lens whose focal length is 4 cm?
Solution:
As the given lens is concave therefore the focal length will be negative.
i.e f = -4 cm
To find the power of lens the formula is,
P = 1 / f
Therefore, Substituting the given values as:
P = 1/-4 cm
= -0.25 D
Hence, the power of the concave lens is -0.25 D.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...