Length of the normal from origin on a straight line whose intercepts are given

Given the intercepts of a straight line on both the axes as m and n. The task is to find the length of the normal on this straight line from the origin.
Examples:

Input: m = 5, n = 3 
Output: 2.57248
Input: m = 13, n = 9 
Output: 7.39973 

Approach: A normal to a line is a line segment drawn from a point perpendicular to the given line. 

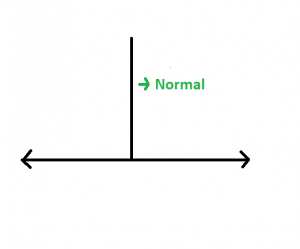
Let p be the length of the normal drawn from the origin to a line, which subtends an angle Θ with the positive direction of x-axis as follows. 

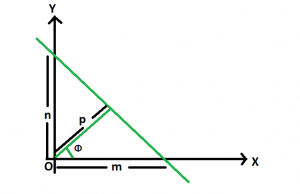
Then, we have cos Θ = p / m and sin Θ = p / n
Since, sin² Θ + cos² Θ = 1
So, (p / m)² + (p / n)² = 1
We get, p = m * n / √(m² + n²)
Below is the implementation of the above approach: 

C++

// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;

// Function to find the normal
// of the straight line
float normal(float m, float n)
{
    // Length of the normal
    float N = (fabsf(m) * fabsf(n))
              / sqrt((fabsf(m) * fabsf(m))
                     + (fabsf(n) * fabsf(n)));

    return N;
}

// Driver code
int main()
{
    float m = -5, n = 3;
    cout << normal(m, n);

    return 0;
}

Java

// Java implementation of the approach
class GFG
{

// Function to find the normal
// of the straight line
static float normal(float m, float n)
{
    // Length of the normal
    float N = (float) ((Math.abs(m) * Math.abs(n))
            / Math.sqrt((Math.abs(m) * Math.abs(m))
                    + (Math.abs(n) * Math.abs(n))));

    return N;
}

// Driver code
public static void main(String[] args)
{
    float m = -5, n = 3;
    System.out.println(normal(m, n));
}
}

// This code has been contributed by 29AjayKumar

Python3

# Python3 implementation of the approach
import math;

# Function to find the normal
# of the straight line
def normal(m, n):

    # Length of the normal
    N = ((abs(m) * abs(n)) /
        math.sqrt((abs(m) * abs(m)) +
                  (abs(n) * abs(n))));

    return N;

# Driver code
m = -5; n = 3;
print(normal(m, n));

# This code is contributed
# by Akanksha Rai

C#

// C# implementation of the approach
using System;

class GFG
{

// Function to find the normal
// of the straight line
static float normal(float m, float n)
{
    // Length of the normal
    float N = (float)((Math.Abs(m) * Math.Abs(n)) /
                       Math.Sqrt((Math.Abs(m) * Math.Abs(m)) +
                                 (Math.Abs(n) * Math.Abs(n))));

    return N;
}

// Driver code
public static void Main()
{
    float m = -5, n = 3;
    Console.Write(normal(m, n));
}
}

// This code is contributed by Akanksha Rai

PHP

<?php
// PHP implementation of the approach

// Function to find the normal
// of the straight line
function normal($m, $n)
{
    // Length of the normal
    $N = (abs($m) * abs($n))  /
              sqrt((abs($m) * abs($m))  +
                   (abs($n) * abs($n)));

    return $N;
}

// Driver code
$m = -5; $n = 3;
echo normal($m, $n);

// This code is contributed by Ryuga
?>

Javascript

<script>

// javascript implementation of the approach


// Function to find the normal
// of the straight line
function normal(m , n)
{
    // Length of the normal
    var N =  ((Math.abs(m) * Math.abs(n))
            / Math.sqrt((Math.abs(m) * Math.abs(m))
                    + (Math.abs(n) * Math.abs(n))));

    return N;
}

// Driver code
var m = -5, n = 3;
document.write(normal(m, n).toFixed(5));

// This code is contributed by Amit Katiyar

</script>

Output:

2.57248

Time Complexity: O(1)
Auxiliary Space: O(1)