Length of diagonals of a Rhombus using length of Side and vertex Angle
Last Updated :
11 May, 2021
Given two integers A and theta, denoting the length of a side of a rhombus and the vertex angle respectively, the task is to find the length of the diagonals of the rhombus.
Examples:
Input: A = 10, theta = 30
Output: 19.32 5.18
Input: A = 6, theta = 45
Output: 11.09 4.59
Approach:
The problem can be solved using the law of cosines. Using the law of cosines on triangles formed by the diagonals and sides of the rhombus gives the following relation to calculate the length of diagonals:
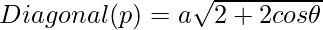
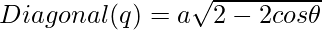

Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
double Length_Diagonals(int a, double theta)
{
double p = a * sqrt(2 + (2 * cos(
theta * (3.141 / 180))));
double q = a * sqrt(2 - (2 * cos(
theta * (3.141 / 180))));
cout << fixed << setprecision(2) << p
<< " " << q;
}
int main()
{
int a = 6;
int theta = 45;
Length_Diagonals(a, theta);
return 0;
}
|
Java
class GFG{
static double[] Length_Diagonals(int a, double theta)
{
double p = a * Math.sqrt(2 + (2 *
Math.cos(theta * (Math.PI / 180))));
double q = a * Math.sqrt(2 - (2 *
Math.cos(theta * (Math.PI / 180))));
return new double[]{ p, q };
}
public static void main(String[] args)
{
int A = 6;
double theta = 45;
double[] ans = Length_Diagonals(A, theta);
System.out.printf("%.2f" + " " + "%.2f",
ans[0], ans[1]);
}
}
|
Python3
import math
def Length_Diagonals(a, theta):
p = a * math.sqrt(2 + (2 * \
math.cos(math.radians(theta))))
q = a * math.sqrt(2 - (2 * \
math.cos(math.radians(theta))))
return [p, q]
A = 6
theta = 45
ans = Length_Diagonals(A, theta)
print(round(ans[0], 2), round(ans[1], 2))
|
C#
using System;
class GFG{
static double[] Length_Diagonals(int a, double theta)
{
double p = a * Math.Sqrt(2 + (2 *
Math.Cos(theta * (Math.PI / 180))));
double q = a * Math.Sqrt(2 - (2 *
Math.Cos(theta * (Math.PI / 180))));
return new double[]{ p, q };
}
public static void Main(String[] args)
{
int A = 6;
double theta = 45;
double[] ans = Length_Diagonals(A, theta);
Console.Write("{0:F2}" + " " + "{1:F2}",
ans[0], ans[1]);
}
}
|
Javascript
<script>
function Length_Diagonals(a, theta)
{
let p = a * Math.sqrt(2 + (2 *
Math.cos(theta * (Math.PI / 180))));
let q = a * Math.sqrt(2 - (2 *
Math.cos(theta * (Math.PI / 180))));
return [ p, q ];
}
let A = 6;
let theta = 45;
let ans = Length_Diagonals(A, theta);
document.write(ans[0].toFixed(2) + " "
+ ans[1].toFixed(2));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...