Length of Diagonals of a Cyclic Quadrilateral using the length of Sides.
Last Updated :
06 Apr, 2023
Given integers A, B, C, and D, denoting the length of sides of a Cyclic Quadrilateral, the task is to find the length of diagonals of a cyclic quadrilateral.
Examples:
Input: A = 10, B = 15, C = 20, D = 25
Output: 22.06 26.07
Input: A = 10, B = 30, C =50, D = 20
Output: 37.93 29.0
Approach: The length of diagonals can be calculated using the following equations:
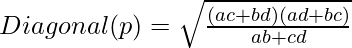 [Tex]Diagonal (q)=\sqrt{\frac{(ac+bd)(ab+cd)}{ad+bc}} [/Tex]
[Tex]Diagonal (q)=\sqrt{\frac{(ac+bd)(ab+cd)}{ad+bc}} [/Tex]

Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
vector<float> Diagonals(int a, int b,
int c, int d)
{
vector<float> ans;
ans.push_back(sqrt(((a * c) + (b * d)) *
((a * d) + (b * c)) /
((a * b) + (c * d))));
ans.push_back(sqrt(((a * c) + (b * d)) *
((a * b) + (c * d)) /
((a * d) + (b * c))));
return ans;
}
int main()
{
int A = 10;
int B = 15;
int C = 20;
int D = 25;
vector<float> ans = Diagonals(A, B, C, D);
printf("%.2f %.2f",
(ans[0]) + .01,
ans[1] + .01);
}
|
Java
import java.util.*;
class GFG{
static Vector<Float> Diagonals(int a, int b,
int c, int d)
{
Vector<Float> ans = new Vector<Float>();
ans.add((float) Math.sqrt(((a * c) + (b * d)) *
((a * d) + (b * c)) /
((a * b) + (c * d))));
ans.add((float) Math.sqrt(((a * c) + (b * d)) *
((a * b) + (c * d)) /
((a * d) + (b * c))));
return ans;
}
public static void main(String[] args)
{
int A = 10;
int B = 15;
int C = 20;
int D = 25;
Vector<Float> ans = Diagonals(A, B,
C, D);
System.out.printf("%.2f %.2f",
(ans.get(0)) + .01,
ans.get(1) + .01);
}
}
|
Python3
import math
def Diagonals(a, b, c, d):
p = math.sqrt(((a * c)+(b * d))*((a * d)+(b * c))
/ ((a * b)+(c * d)))
q = math.sqrt(((a * c)+(b * d))*((a * b)+(c * d))
/ ((a * d)+(b * c)))
return [p, q]
A = 10
B = 15
C = 20
D = 25
ans = Diagonals(A, B, C, D)
print(round(ans[0], 2), round(ans[1], 2))
|
C#
using System;
using System.Collections.Generic;
class GFG{
static List<float> Diagonals(int a, int b,
int c, int d)
{
List<float> ans = new List<float>();
ans.Add((float) Math.Sqrt(((a * c) + (b * d)) *
((a * d) + (b * c)) /
((a * b) + (c * d))));
ans.Add((float) Math.Sqrt(((a * c) + (b * d)) *
((a * b) + (c * d)) /
((a * d) + (b * c))));
return ans;
}
public static void Main(String[] args)
{
int A = 10;
int B = 15;
int C = 20;
int D = 25;
List<float> ans = Diagonals(A, B,
C, D);
Console.Write("{0:F2} {1:F2}",
(ans[0]) + .01,
ans[1] + .01);
}
}
|
Javascript
<script>
function Diagonals(a, b, c, d)
{
var p = parseFloat(
Math.sqrt(((a * c) + (b * d)) *
((a * d) + (b * c)) /
((a * b) + (c * d))));
var q = parseFloat(
Math.sqrt(((a * c) + (b * d)) *
((a * b) + (c * d)) /
((a * d) + (b * c))));
return [p, q];
}
var A = 10;
var B = 15;
var C = 20;
var D = 25;
var ans = Diagonals(A, B, C, D)
document.write(ans[0].toFixed(2) + " ",
ans[1].toFixed(2));
</script>
|
Time Complexity: O(log n)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...