Leibniz harmonic triangle
Last Updated :
19 Jul, 2022
The Leibniz harmonic triangle is a triangular arrangement of unit fractions in which the outermost diagonals consist of the reciprocals of the row numbers and each inner cell is the cell diagonally above and to the left minus the cell to the left. To put it algebraically, L(r, 1) = 1/r, where r is the number of the row, starting from 1, and c is the number, never more than r and L(r, c) = L(r – 1, c – 1) – L(r, c – 1).

Relation with pascal’s triangle
Whereas each entry in Pascal’s triangle is the sum of the two entries in the above row, each entry in the Leibniz triangle is the sum of the two entries in the row below it. For example, in the 5th row, the entry (1/30) is the sum of the two (1/60)s in the 6th row.
Just as Pascal’s triangle can be computed by using binomial coefficients, so can Leibniz’s:
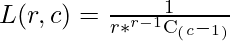
Properties
If one takes the denominators of the nth row and adds them, then the result will equal n.2n-1. For example, for the 3rd row, we have 3 + 6 + 3 = 12 = 3 × 22.
Given a positive integer n. The task is to print Leibniz harmonic triangle of height n.
Examples:
Input : n = 4
Output :
1
1/2 1/2
1/3 1/6 1/3
1/4 1/12 1/12 1/4
Input : n = 3
Output :
1
1/2 1/2
1/3 1/6 1/3
Below is the implementation of printing Leibniz harmonic triangle of height n based on above relation with Pascal triangle.
C++
#include <bits/stdc++.h>
using namespace std;
void LeibnizHarmonicTriangle(int n)
{
int C[n + 1][n + 1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= min(i, n); j++) {
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++)
cout << "1/" << i * C[i - 1][j - 1] << " ";
cout << endl;
}
}
int main()
{
int n = 4;
LeibnizHarmonicTriangle(n);
return 0;
}
|
Java
import java.io.*;
import java.math.*;
class GFG {
static void LeibnizHarmonicTriangle(int n)
{
int C[][] = new int[n + 1][n + 1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= Math.min(i, n);
j++) {
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = C[i - 1][j - 1] +
C[i - 1][j];
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++)
System.out.print("1/" + i * C[i - 1][j - 1]
+ " ");
System.out.println();
}
}
public static void main(String args[])
{
int n = 4;
LeibnizHarmonicTriangle(n);
}
}
|
Python3
def LeibnizHarmonicTriangle(n):
C = [[0 for x in range(n + 1)]
for y in range(n + 1)];
for i in range(0, n + 1):
for j in range(0, min(i, n) + 1):
if (j == 0 or j == i):
C[i][j] = 1;
else:
C[i][j] = (C[i - 1][j - 1] +
C[i - 1][j]);
for i in range(1, n + 1):
for j in range(1, i + 1):
print("1/", end = "");
print(i * C[i - 1][j - 1],
end = " ");
print();
LeibnizHarmonicTriangle(4);
|
C#
using System;
class GFG {
static void LeibnizHarmonicTriangle(int n)
{
int [,]C = new int[n + 1,n + 1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= Math.Min(i, n);
j++) {
if (j == 0 || j == i)
C[i,j] = 1;
else
C[i,j] = C[i - 1,j - 1] +
C[i - 1,j];
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++)
Console.Write("1/" + i * C[i - 1,j - 1]
+ " ");
Console.WriteLine();
}
}
public static void Main()
{
int n = 4;
LeibnizHarmonicTriangle(n);
}
}
|
PHP
<?php
function LeibnizHarmonicTriangle($n)
{
for ($i = 0; $i <= $n; $i++)
{
for ($j = 0; $j <= min($i, $n); $j++)
{
if ($j == 0 || $j == $i)
$C[$i][$j] = 1;
else
$C[$i][$j] = $C[$i - 1][$j - 1] +
$C[$i - 1][$j];
}
}
for ($i = 1; $i <= $n; $i++)
{
for ($j = 1; $j <= $i; $j++)
echo "1/", $i * $C[$i - 1][$j - 1], " ";
echo "\n";
}
}
$n = 4;
LeibnizHarmonicTriangle($n);
?>
|
Javascript
<script>
function LeibnizHarmonicTriangle(n)
{
let C = new Array(n + 1);
for (let i = 0; i < C.length; i++) {
C[i] = new Array(2);
}
for (let i = 0; i <= n; i++) {
for (let j = 0; j <= Math.min(i, n);
j++) {
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = C[i - 1][j - 1] +
C[i - 1][j];
}
}
for (let i = 1; i <= n; i++)
{
for (let j = 1; j <= i; j++)
document.write("1/" + i * C[i - 1][j - 1]
+ " ");
document.write("<br/>");
}
}
let n = 4;
LeibnizHarmonicTriangle(n);
</script>
|
Output:
1/1
1/2 1/2
1/3 1/6 1/3
1/4 1/12 1/12 1/4
Time complexity: O(n2) for given n
Auxiliary Space: O(n2)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...