Learning Vector Quantization
Last Updated :
07 Jan, 2023
Learning Vector Quantization ( or LVQ ) is a type of Artificial Neural Network which also inspired by biological models of neural systems. It is based on prototype supervised learning classification algorithm and trained its network through a competitive learning algorithm similar to Self Organizing Map. It can also deal with the multiclass classification problem. LVQ has two layers, one is the Input layer and the other one is the Output layer. The architecture of the Learning Vector Quantization with the number of classes in an input data and n number of input features for any sample is given below: 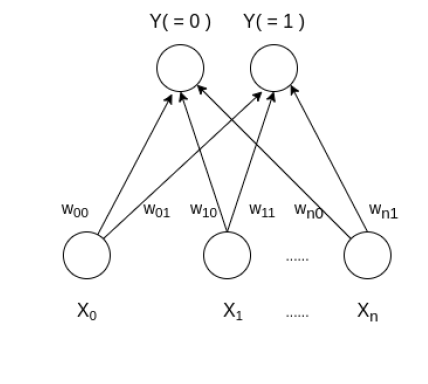
How Learning Vector Quantization works?
Let’s say that an input data of size ( m, n ) where m is the number of training examples and n is the number of features in each example and a label vector of size ( m, 1 ). First, it initializes the weights of size ( n, c ) from the first c number of training samples with different labels and should be discarded from all training samples. Here, c is the number of classes. Then iterate over the remaining input data, for each training example, it updates the winning vector ( weight vector with the shortest distance ( e.g Euclidean distance ) from the training example ).
The weight updation rule is given by:
if correctly_classified:
wij(new) = wij(old) + alpha(t) * (xik - wij(old))
else:
wij(new) = wij(old) - alpha(t) * (xik - wij(old))
where alpha is a learning rate at time t, j denotes the winning vector, i denotes the ith feature of training example and k denotes the kth training example from the input data. After training the LVQ network, trained weights are used for classifying new examples. A new example is labelled with the class of the winning vector.
Algorithm:
Step 1: Initialize reference vectors.
from a given set of training vectors, take the first “n” number of clusters training vectors and use them as weight vectors, the remaining vectors can be used for training.
Assign initial weights and classifications randomly
Step 2: Calculate Euclidean distance for i=1 to n and j=1 to m,
D(j) = ΣΣ (xi-Wij)^2
find winning unit index j, where D(j) is minimum
Step 3: Update weights on the winning unit wi using the following conditions:
if T = J then wi(new) = wi (old) + α[x – wi(old)]
if T ≠ J then wi(new) = wi (old) – α[x – wi(old)]
Step 4: Check for the stopping condition if false repeat the above steps.
Below is the implementation.
Python3
import math
class LVQ :
def winner( self, weights, sample ) :
D0 = 0
D1 = 0
for i in range( len( sample ) ) :
D0 = D0 + math.pow( ( sample[i] - weights[0][i] ), 2 )
D1 = D1 + math.pow( ( sample[i] - weights[1][i] ), 2 )
if D0 > D1 :
return 0
else :
return 1
def update( self, weights, sample, J, alpha, actual ) :
if actual -- j:
for i in range(len(weights)) :
weights[J][i] = weights[J][i] + alpha * ( sample[i] - weights[J][i] )
else:
for i in range(len(weights)) :
weights[J][i] = weights[J][i] - alpha * ( sample[i] - weights[J][i] )
def main() :
X = [[ 0, 0, 1, 1 ], [ 1, 0, 0, 0 ],
[ 0, 0, 0, 1 ], [ 0, 1, 1, 0 ],
[ 1, 1, 0, 0 ], [ 1, 1, 1, 0 ],]
Y = [ 0, 1, 0, 1, 1, 1 ]
m, n = len( X ), len( X[0] )
weights = []
weights.append( X.pop( 0 ) )
weights.append( X.pop( 0 ) )
m = m - 2
Y.pop(0)
Y.pop(0)
ob = LVQ()
epochs = 3
alpha = 0.1
for i in range( epochs ) :
for j in range( m ) :
T = X[j]
J = ob.winner( weights, T )
ob.update( weights, T, J, alpha , Y[j])
T = [ 0, 0, 1, 0 ]
J = ob.winner( weights, T )
print( "Sample T belongs to class : ", J )
print( "Trained weights : ", weights )
if __name__ == "__main__":
main()
|
Output:Sample T belongs to class : 0 Trained weights : [[0.3660931, 0.38165410000000005, 1, 1], [0.33661, 0.34390000000000004, 0, 1]]
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...