LCM of N numbers modulo M

Given an array arr[] of integers, the task is to find the LCM of all the elements of the array modulo M where M = 10⁹ + 7.
Examples:

Input: arr[] = {10000000, 12345, 159873} 
Output: 780789722 
LCM of (10000000, 12345, 159873) is 1315754790000000 
1315754790000000 % 1000000007 = 780789722
Input: arr[] = {10, 13, 15} 
Output: 390 

Approach: If you have gone through the post that calculates LCM of array elements, the first approach that comes to mind is to take modulo at every step when LCM of ans and arr[i] is being calculated. 

ans = 1 
// For i = 1 to n – 1 
ans = lcm(ans, arr[i]) % 1000000007 // Wrong approach 

However, this approach is wrong and the mistake can be realized in the following example:  

Take M = 41 and arr[] = {13, 18, 30}
Incorrect solution: 
LCM(13, 18, 30) % 41 
LCM(LCM(13, 18) % 41, 30) % 41 
LCM(234 % 41, 30) % 41 
LCM(29, 30) % 41 
870 % 41 
9
Correct solution: 
LCM(13, 18, 30) % 41 
LCM(LCM(13, 18), 30) % 41 
LCM(234, 30) % 41 
1170 % 41 
22 

Note: Whenever the LCM of 2 numbers becomes > M, the approach doesn’t work.
The correct approach is to prime factorize the elements of the array and keep track of the highest power of every prime for each element. LCM will be the product of these primes raised to their highest power in the array.
Illustration: 

Let elements be [36, 480, 500, 343] 
Prime factorization results: 
36 = 2² * 3²
480 = 2⁵ * 3 * 5 
500 = 2² * 5³
343 = 7³
Highest power of 2 amongst all array elements = Max(2, 5, 2, 0) = 5 
Highest power of 3 amongst all array elements = Max(2, 1, 0, 0) = 2 
Highest power of 5 amongst all array elements = Max(0, 1, 3, 0) = 3 
Highest power of 7 amongst all array elements = Max(0, 0, 0, 3) = 3
Therefore, LCM = 2⁵ * 3² * 5³ * 7³ = 12348000 

Let p be a prime factor of an element of the array and x be its highest power in the whole array. Then,

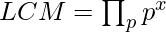
Using the above formula, we can easily calculate the LCM of the whole array and our problem of MOD will also be solved. Simplifying the expression, we get:

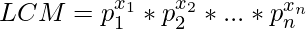
Since modulo operation is distributive over multiplication, we can safely write the following expression. 

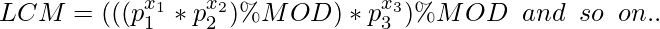
Now, the problem arises as to how to compute prime factors and their powers efficiently. For that, we can use the sieve of Eratosthenes. Refer to this post: Using Sieve to compute prime factors and their powers.
Below is the implementation of the above approach: 

C++

// C++ program to compute LCM of array elements modulo M
#include <bits/stdc++.h>
#define F first
#define S second
#define MAX 10000003
using namespace std;

typedef long long ll;
const int mod = 1000000007;

int prime[MAX];
unordered_map<int, int> max_map;

// Function to return a^n
int power(int a, int n)
{
    if (n == 0)
        return 1;
    int p = power(a, n / 2) % mod;
    p = (p * p) % mod;
    if (n & 1)
        p = (p * a) % mod;
    return p;
}

// Function to find the smallest prime factors
// of numbers upto MAX
void sieve()
{
    prime[0] = prime[1] = 1;
    for (int i = 2; i < MAX; i++) {
        if (prime[i] == 0) {
            for (int j = i * 2; j < MAX; j += i) {
                if (prime[j] == 0) {
                    prime[j] = i;
                }
            }
            prime[i] = i;
        }
    }
}

// Function to return the LCM modulo M
ll lcmModuloM(const int* ar, int n)
{

    for (int i = 0; i < n; i++) {
        int num = ar[i];
        unordered_map<int, int> temp;

        // Temp stores mapping of prime factor to
        // its power for the current element
        while (num > 1) {

            // Factor is the smallest prime factor of num
            int factor = prime[num];

            // Increase count of factor in temp
            temp[factor]++;

            // Reduce num by its prime factor
            num /= factor;
        }

        for (auto it : temp) {

            // Store the highest power of every prime
            // found till now in a new map max_map
            max_map[it.first] = max(max_map[it.first], it.second);
        }
    }

    ll ans = 1;

    for (auto it : max_map) {

        // LCM is product of primes to their highest powers modulo M
        ans = (ans * power(it.F, it.S)) % mod;
    }

    return ans;
}

// Driver code
int main()
{
    sieve();
    int arr[] = { 36, 500, 480, 343 };
    int n = sizeof(arr) / sizeof(arr[0]);
    cout << lcmModuloM(arr, n);
    return 0;
}

Java

// Java program to compute LCM of
// array elements modulo M
import java.util.*;

class GFG{

final static int MAX = 10000003;
final static int mod = 1000000007;
static int[] prime = new int[MAX];

// Function to return a^n
public static int power(int a, int n)
{
    if(n == 0)
       return 1;

    int p = power(a, n / 2) % mod;
    p = (p * p) % mod;

    if((n & 1) > 0)
       p = (p * a) % mod;

    return p;
}

// Function to find the smallest prime
// factors of numbers upto MAX
public static void sieve()
{
    prime[0] = 1;
    prime[1] = 1;

    for(int i = 2; i < MAX; i++)
    {
       if(prime[i] == 0)
       {
           for(int j = i * 2;
                   j < MAX; j += i)
           {
              if(prime[j] == 0)
              {
                  prime[j] = i;
              }
           }
           prime[i] = i;
       }
    }
}

// Function to return the LCM modulo M
public static long lcmModuloM(int[] arr, int n)
{
    HashMap<Integer,
            Integer> maxMap = new HashMap<>();

    for(int i = 0; i < n; i++)
    {
        HashMap<Integer,
                Integer> temp = new HashMap<>();
        int num = arr[i];

        // Temp stores mapping of prime
        // factor to its power for the
        // current element
        while(num > 1)
        {

            // Factor is the smallest prime
            // factor of num
            int factor = prime[num];

            if(temp.containsKey(factor))
               temp.put(factor, temp.get(factor) + 1);
            else
               temp.put(factor, 1);

            // Factor is the smallest prime
            // factor of num
            num = num / factor;
        }

        for(Map.Entry<Integer,
                      Integer> m : temp.entrySet())
        {
           if(maxMap.containsKey(m.getKey()))
           {
               int maxPower = Math.max(m.getValue(),
                                       maxMap.get(
                                       m.getKey()));
               maxMap.put(m.getKey(), maxPower);
           }
           else
           {
               maxMap.put(m.getKey(),m.getValue());
           }
        }
    }

    long ans = 1;
    for(Map.Entry<Integer,
                  Integer> m : maxMap.entrySet())
    {

       // LCM is product of primes to their
       // highest powers modulo M
       ans = (ans * power(m.getKey(),
                          m.getValue()) % mod);
    }

    return ans;
}

// Driver code
public static void main(String[] args)
{
    sieve();
    int[] arr = new int[]{36, 500, 480, 343 };
    int n = arr.length;

    System.out.println(lcmModuloM(arr, n));
}
}

// This code is contributed by parshavnahta97

Python3

# Python3 program to compute LCM of
# array elements modulo M
MAX = 10000003

mod = 1000000007

prime = [0 for i in range(MAX)]

max_map = dict()

# function to return a^n
def power(a, n):

    if n == 0:
        return 1
    p = power(a, n // 2) % mod
    p = (p * p) % mod

    if n & 1:
        p = (p * a) % mod
    return p

# function to find the smallest prime
# factors of numbers upto MAX
def sieve():
    prime[0], prime[1] = 1, 1
    for i in range(2, MAX):
        if prime[i] == 0:
            for j in range(i * 2, MAX, i):
                if prime[j] == 0:
                    prime[j] = i
            prime[i] = i

# function to return the LCM modulo M
def lcmModuloM(arr, n):

    for i in range(n):
        num = arr[i]

        temp = dict()

        # temp stores mapping of prime factors
        # to its power for the current element
        while num > 1:

            # factor is the smallest prime
            # factor of num
            factor = prime[num]

            # Increase count of factor in temp
            if factor in temp.keys():
                temp[factor] += 1
            else:
                temp[factor] = 1

            # Reduce num by its prime factor
            num = num // factor

        for i in temp:
            # store the highest power of every prime
            # found till now in a new map max_map
            if i in max_map.keys():
                max_map[i] = max(max_map[i], temp[i])
            else:
                max_map[i] = temp[i]

    ans = 1

    for i in max_map:

        # LCM is product of primes to their
        # highest powers modulo M
        ans = (ans * power(i, max_map[i])) % mod
    return ans

# Driver code
sieve()
arr = [36, 500, 480, 343]
n = len(arr)
print(lcmModuloM(arr, n))

# This code is contributed
# by Mohit kumar 29

C#

// C# program to compute LCM of
// array elements modulo M
using System;
using System.Collections.Generic;
class GFG{

readonly static int MAX = 10000003;
readonly static int mod = 1000000007;
static int[] prime = new int[MAX];

// Function to return a^n
public static int power(int a,
                        int n)
{
  if(n == 0)
    return 1;

  int p = power(a, n / 2) %
          mod;
  p = (p * p) % mod;

  if((n & 1) > 0)
    p = (p * a) % mod;

  return p;
}

// Function to find the smallest
// prime factors of numbers upto
// MAX
public static void sieve()
{
  prime[0] = 1;
  prime[1] = 1;

  for(int i = 2; i < MAX; i++)
  {
    if(prime[i] == 0)
    {
      for(int j = i * 2;
              j < MAX; j += i)
      {
        if(prime[j] == 0)
        {
          prime[j] = i;
        }
      }
      prime[i] = i;
    }
  }
}

// Function to return the
// LCM modulo M
public static long lcmModuloM(int[] arr,
                              int n)
{
  Dictionary<int,
             int> maxMap =
             new Dictionary<int,
                            int>();

  for(int i = 0; i < n; i++)
  {
    Dictionary<int,
               int> temp =
               new Dictionary<int,
                              int>();
    int num = arr[i];

    // Temp stores mapping of prime
    // factor to its power for the
    // current element
    while(num > 1)
    {
      // Factor is the smallest
      // prime factor of num
      int factor = prime[num];

      if(temp.ContainsKey(factor))
        temp[factor]++;
      else
        temp.Add(factor, 1);

      // Factor is the smallest
      // prime factor of num
      num = num / factor;
    }

    foreach(KeyValuePair<int,
                         int> m in temp)
    {
      if(maxMap.ContainsKey(m.Key))
      {
        int maxPower = Math.Max(m.Value,
                                maxMap[m.Key]);
        maxMap[m.Key] = maxPower;
      }
      else
      {
        maxMap.Add(m.Key,m.Value);
      }
    }
  }

  long ans = 1;
  foreach(KeyValuePair<int,
                       int> m in maxMap)
  {
    // LCM is product of primes to their
    // highest powers modulo M
    ans = (ans * power(m.Key,
                       m.Value) %
                       mod);
  }

  return ans;
}

// Driver code
public static void Main(String[] args)
{
  sieve();
  int[] arr = new int[]{36, 500,
                        480, 343};
  int n = arr.Length;
  Console.WriteLine(lcmModuloM(arr, n));
}
}

// This code is contributed by 29AjayKumar

Javascript

<script>

// Javascript program to compute LCM of
// array elements modulo M
let MAX = 10000003;
let mod = 1000000007;
let prime = new Array(MAX);
for(let i = 0; i < MAX; i++)
{
    prime[i] = 0;
}

// Function to return a^n
function power(a, n)
{
    if(n == 0)
       return 1;

    let p = power(a, n / 2) % mod;
    p = (p * p) % mod;

    if((n & 1) > 0)
       p = (p * a) % mod;

    return p;
}

// Function to find the smallest prime
// factors of numbers upto MAX
function sieve()
{
    prime[0] = 1;
    prime[1] = 1;

    for(let i = 2; i < MAX; i++)
    {
       if(prime[i] == 0)
       {
           for(let j = i * 2;
                   j < MAX; j += i)
           {
              if(prime[j] == 0)
              {
                  prime[j] = i;
              }
           }
           prime[i] = i;
       }
    }
}

// Function to return the LCM modulo M
function lcmModuloM(arr,n)
{
    let maxMap = new Map();

    for(let i = 0; i < n; i++)
    {
        let temp = new Map();
        let num = arr[i];

        // Temp stores mapping of prime
        // factor to its power for the
        // current element
        while(num > 1)
        {

            // Factor is the smallest prime
            // factor of num
            let factor = prime[num];

            if(temp.has(factor))
               temp.set(factor, temp.get(factor) + 1);
            else
               temp.set(factor, 1);

            // Factor is the smallest prime
            // factor of num
            num = num / factor;
        }

        for(let [key, value] of temp.entries())
        {
           if(maxMap.has(key))
           {
               let maxPower = Math.max(value,
                                       maxMap.get(
                                       key));
               maxMap.set(key, maxPower);
           }
           else
           {
               maxMap.set(key,value);
           }
        }
    }

    let ans = 1;
    for(let [key, value] of maxMap.entries())
    {

       // LCM is product of primes to their
       // highest powers modulo M
       ans = (ans * power(key,
                          value) % mod);
    }
    return ans;
}

// Driver code
sieve();
let arr = [36, 500, 480, 343];
let n = arr.length;
document.write(lcmModuloM(arr, n));

// This code is contributed by unknown2108.
</script>

Output:

12348000

The above code works for the following constraints:

References: https://stackoverflow.com/questions/16633449/calculate-lcm-of-n-numbers-modulo-1000000007