Largest subset of Graph vertices with edges of 2 or more colors
Last Updated :
13 Sep, 2023
Given an undirected complete graph with N nodes or vertices. Edges of the graph are colored, find the largest subset of vertices with edges of 2 or more colors. We are given graph as adjacency matrix C[][] where C[i][j] is color of edge from vertex i to vertex j. Since graph is undirected, values C[i][j] of C[j][i] are same.
We define C[i][i] to be zero, although there is no such edge present. i.e. the graph does not contain self-loops.
Examples:
Example 1:
Input : C[][]= {{0, 1, 2},
{1, 0, 3},
{2, 3, 0}}
Output : 3

Example 2:
Input : C[][]= {{0, 1, 1},
{1, 0, 3},
{1, 3, 0}}
Output : 0

Since graph is complete, each edge can be one of n*(n-1)/2 +1 different colors. These colors are labeled from 0 to n*(n-1)/2, inclusive. But not all these n*(n-1)/2 +1 colors need to be used. i.e., it is possible that two different edges could have the same color.
Let’s call a vertex “bad” if all its neighbors are of the same color. Obviously, we can’t have any such bad vertex in our subset, so remove such bad vertex from the graph. This might introduce some more bad vertices, but we can keep repeating this process until we find a subset free of bad vertices. So, at last, we should remain through a graph which does not have any bad vertex means every vertex of our subset has at least two different color edges with other adjacent vertices.
Example:
Input :
let C[6][6]:
{{0, 9, 2, 4, 7, 8},
{9, 0, 9, 9, 7, 9},
{2, 9, 0, 3, 7, 6},
{4, 9, 3, 0, 7, 1},
{7, 7, 7, 7, 0, 7},
{8, 9, 6, 1, 7, 0}};

Step I: First of all, we can see that row 5(node ‘e’) contains only 7 means node ‘e’ is connected through edges having color code 7 so it does not have more than one color edge so we have to remove 5 from subset. Now, our graph will contain only 5 vertex and are as:
C[5][5]:
{{0, 9, 2, 4, 8},
{9, 0, 9, 9, 9},
{2, 9, 0, 3, 6},
{4, 9, 3, 0, 1},
{8, 9, 6, 1, 0}};
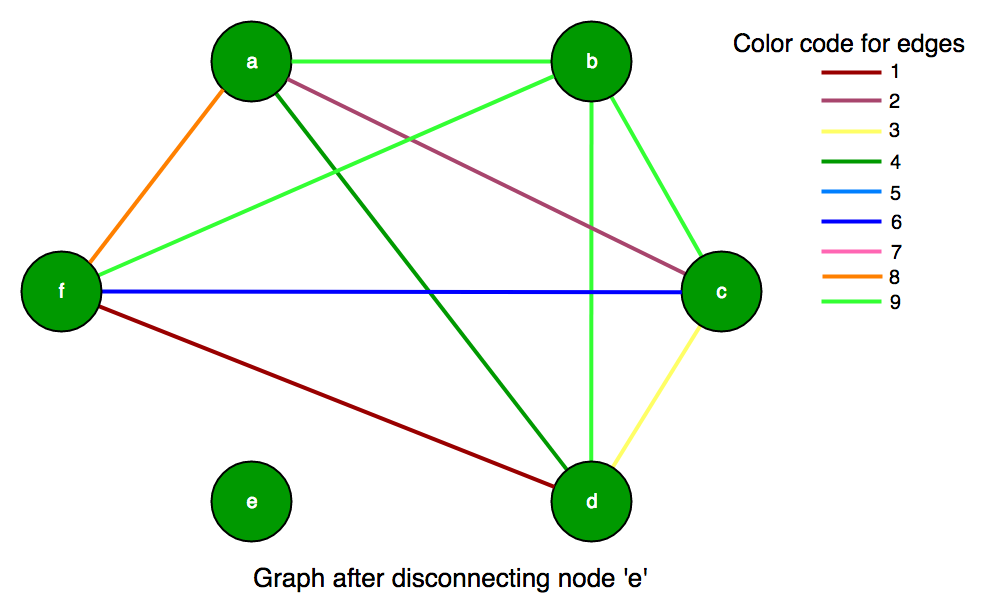
Step II: Further, we can see that row 2 (node ‘b’) also doesn’t contain more than 1 color edge, so we should remove row 2 and column 2 also. Which result in our new graph as:
C[4][4]:
{{0, 2, 4, 8},
{2, 0, 3, 6},
{4, 3, 0, 1},
{8, 6, 1, 0}};

Step III: Now, we can see that each vertex has more than 1 different color edge. So, the total number of vertices in the subset is 4.
Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
const int N = 6;
int subsetGraph(int C[][N])
{
set<int> vertices;
for (int i = 0; i < N; ++i)
vertices.insert(i);
while (!vertices.empty())
{
if (vertices.size() == 1)
return 1;
bool someone_removed = false;
for (int x : vertices)
{
set<int> values;
for (int y : vertices)
if (y != x)
values.insert(C[x][y]);
if (values.size() == 1)
{
vertices.erase(x);
someone_removed = true;
break;
}
}
if (!someone_removed)
break;
}
return (vertices.size());
}
int main()
{
int C[][N] = {{0, 9, 2, 4, 7, 8},
{9, 0, 9, 9, 7, 9},
{2, 9, 0, 3, 7, 6},
{4, 9, 3, 0, 7, 1},
{7, 7, 7, 7, 0, 7},
{8, 9, 6, 1, 7, 0}
};
cout << subsetGraph(C);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static int N = 6;
static int subsetGraph(int C[][])
{
HashSet<Integer> vertices = new HashSet<>();
for (int i = 0; i < N; ++i)
{
vertices.add(i);
}
while (!vertices.isEmpty())
{
if (vertices.size() == 1)
{
return 1;
}
boolean someone_removed = false;
for (int x : vertices)
{
HashSet<Integer> values = new HashSet<>();
for (int y : vertices)
{
if (y != x)
{
values.add(C[x][y]);
}
}
if (values.size() == 1)
{
vertices.remove(x);
someone_removed = true;
break;
}
}
if (!someone_removed)
{
break;
}
}
return (vertices.size());
}
public static void main(String[] args)
{
int C[][] = {{0, 9, 2, 4, 7, 8},
{9, 0, 9, 9, 7, 9},
{2, 9, 0, 3, 7, 6},
{4, 9, 3, 0, 7, 1},
{7, 7, 7, 7, 0, 7},
{8, 9, 6, 1, 7, 0}
};
System.out.println(subsetGraph(C));
}
}
|
Python3
def subsetGraph(C):
global N
vertices = set()
for i in range(N):
vertices.add(i)
while (len(vertices) != 0):
if (len(vertices) == 1):
return 1
someone_removed = False
for x in vertices:
values = set()
for y in vertices:
if (y != x):
values.add(C[x][y])
if (len(values) == 1):
vertices.remove(x)
someone_removed = True
break
if (not someone_removed):
break
return len(vertices)
N = 6
C = [[0, 9, 2, 4, 7, 8],
[9, 0, 9, 9, 7, 9],
[2, 9, 0, 3, 7, 6],
[4, 9, 3, 0, 7, 1],
[7, 7, 7, 7, 0, 7],
[8, 9, 6, 1, 7, 0]]
print(subsetGraph(C))
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static int N = 6;
static int subsetGraph(int [,]C)
{
HashSet<int> vertices = new HashSet<int>();
for (int i = 0; i < N; ++i)
{
vertices.Add(i);
}
while (vertices.Count != 0)
{
if (vertices.Count == 1)
{
return 1;
}
Boolean someone_removed = false;
foreach (int x in vertices)
{
HashSet<int> values = new HashSet<int>();
foreach (int y in vertices)
{
if (y != x)
{
values.Add(C[x, y]);
}
}
if (values.Count == 1)
{
vertices.Remove(x);
someone_removed = true;
break;
}
}
if (!someone_removed)
{
break;
}
}
return (vertices.Count);
}
public static void Main(String[] args)
{
int [,]C = {{0, 9, 2, 4, 7, 8},
{9, 0, 9, 9, 7, 9},
{2, 9, 0, 3, 7, 6},
{4, 9, 3, 0, 7, 1},
{7, 7, 7, 7, 0, 7},
{8, 9, 6, 1, 7, 0}};
Console.WriteLine(subsetGraph(C));
}
}
|
Javascript
<script>
let N = 6;
function subsetGraph(C)
{
let vertices = new Set();
for(let i = 0; i < N; ++i)
{
vertices.add(i);
}
while (vertices.size != 0)
{
if (vertices.size == 1)
{
return 1;
}
let someone_removed = false;
for(let x of vertices.values())
{
let values = new Set();
for(let y of vertices.values())
{
if (y != x)
{
values.add(C[x][y]);
}
}
if (values.size == 1)
{
vertices.delete(x);
someone_removed = true;
break;
}
}
if (!someone_removed)
{
break;
}
}
return (vertices.size);
}
let C = [ [ 0, 9, 2, 4, 7, 8 ],
[ 9, 0, 9, 9, 7, 9 ],
[ 2, 9, 0, 3, 7, 6 ],
[ 4, 9, 3, 0, 7, 1 ],
[ 7, 7, 7, 7, 0, 7 ],
[ 8, 9, 6, 1, 7, 0 ] ];
document.write(subsetGraph(C));
</script>
|
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...