Largest subset of Graph vertices with edges of 2 or more colors

Given an undirected complete graph with N nodes or vertices. Edges of the graph are colored, find the largest subset of vertices with edges of 2 or more colors. We are given graph as adjacency matrix C[][] where C[i][j] is color of edge from vertex i to vertex j. Since graph is undirected, values C[i][j] of C[j][i] are same.

We define C[i][i] to be zero, although there is no such edge present. i.e. the graph does not contain self-loops.

Examples:

Example 1: 

Input : C[][]= {{0, 1, 2},

                {1, 0, 3},

                {2, 3, 0}} 

Output : 3

Example 2: 

Input  : C[][]= {{0, 1, 1},

                {1, 0, 3},

                {1, 3, 0}} 

Output : 0

Since graph is complete, each edge can be one of n*(n-1)/2 +1 different colors. These colors are labeled from 0 to n*(n-1)/2, inclusive. But not all these n*(n-1)/2 +1 colors need to be used. i.e., it is possible that two different edges could have the same color.  

Let’s call a vertex “bad” if all its neighbors are of the same color. Obviously, we can’t have any such bad vertex in our subset, so remove such bad vertex from the graph. This might introduce some more bad vertices, but we can keep repeating this process until we find a subset free of bad vertices. So, at last, we should remain through a graph which does not have any bad vertex means every vertex of our subset has at least two different color edges with other adjacent vertices.

Example:
Input : 
let C[6][6]: 
{{0, 9, 2, 4, 7, 8}, 
{9, 0, 9, 9, 7, 9}, 
{2, 9, 0, 3, 7, 6}, 
{4, 9, 3, 0, 7, 1}, 
{7, 7, 7, 7, 0, 7}, 
{8, 9, 6, 1, 7, 0}}; 

Step I: First of all, we can see that row 5(node ‘e’) contains only 7 means node ‘e’ is connected through edges having color code 7 so it does not have more than one color edge so we have to remove 5 from subset. Now, our graph will contain only 5 vertex and are as: 
C[5][5]: 
{{0, 9, 2, 4, 8}, 
{9, 0, 9, 9, 9}, 
{2, 9, 0, 3, 6}, 
{4, 9, 3, 0, 1}, 
{8, 9, 6, 1, 0}}; 

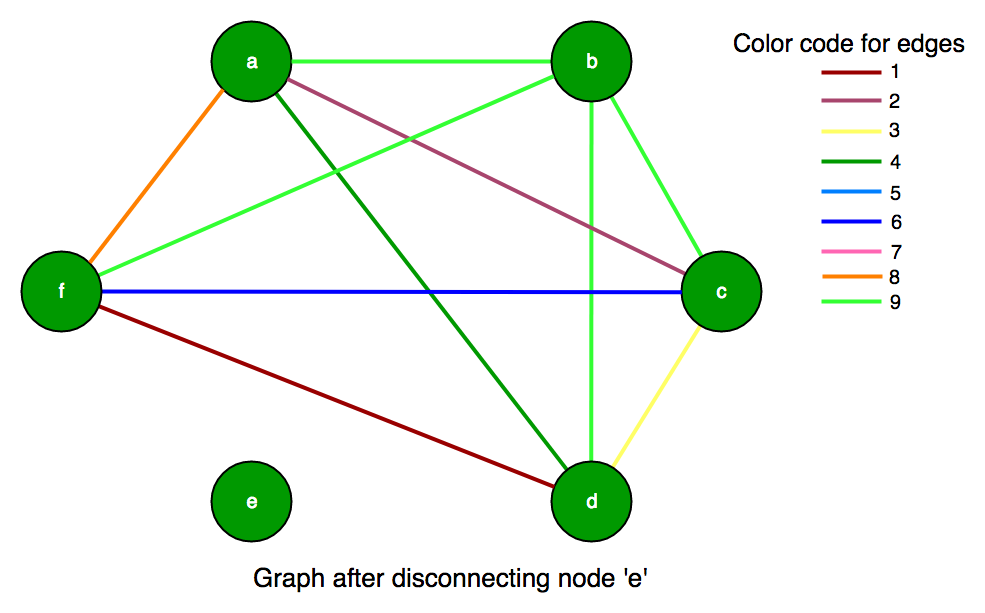
Step II: Further, we can see that row 2 (node ‘b’) also doesn’t contain more than 1 color edge, so we should remove row 2 and column 2 also. Which result in our new graph as: 
C[4][4]: 
{{0, 2, 4, 8}, 
{2, 0, 3, 6}, 
{4, 3, 0, 1}, 
{8, 6, 1, 0}}; 

Step III: Now, we can see that each vertex has more than 1 different color edge. So, the total number of vertices in the subset is 4.

Implementation:

C++

// C++ program to find size of subset of graph vertex
// such that each vertex has more than 1 color edges
#include <bits/stdc++.h>
using namespace std;

// Number of vertices
const int N = 6;

// function to calculate max subset size
int subsetGraph(int C[][N])
{
    // set for number of vertices
    set<int> vertices;
    for (int i = 0; i < N; ++i)
        vertices.insert(i);

    // loop for deletion of vertex from set
    while (!vertices.empty())
    {
        // if subset has only 1 vertex return 0
        if (vertices.size() == 1)
            return 1;

        // for each vertex iterate and keep removing
        // a vertex while we find a vertex with all
        // edges of same color.
        bool someone_removed = false;
        for (int x : vertices)
        {
            // note down different color values
            // for each vertex
            set<int> values;
            for (int y : vertices)
                if (y != x)
                    values.insert(C[x][y]);

            // if only one color is found
            // erase that vertex (bad vertex)
            if (values.size() == 1)
            {
                vertices.erase(x);
                someone_removed = true;
                break;
            }
        }

        // If no vertex was removed in the
        // above loop.
        if (!someone_removed)
            break;
    }

    return (vertices.size());
}

// Driver program
int main()
{
    int C[][N] = {{0, 9, 2, 4, 7, 8},
        {9, 0, 9, 9, 7, 9},
        {2, 9, 0, 3, 7, 6},
        {4, 9, 3, 0, 7, 1},
        {7, 7, 7, 7, 0, 7},
        {8, 9, 6, 1, 7, 0}
    };
    cout << subsetGraph(C);
    return 0;
}

Java

// Java program to find size of
// subset of graph vertex such that
// each vertex has more than 1 color edges
import java.util.*;

class GFG
{

    // Number of vertices
    static int N = 6;

    // function to calculate max subset size
    static int subsetGraph(int C[][])
    {
        // set for number of vertices
        HashSet<Integer> vertices = new HashSet<>();
        for (int i = 0; i < N; ++i)
        {
            vertices.add(i);
        }

        // loop for deletion of vertex from set
        while (!vertices.isEmpty())
        {

            // if subset has only 1 vertex return 0
            if (vertices.size() == 1)
            {
                return 1;
            }

            // for each vertex iterate and keep removing
            // a vertex while we find a vertex with all
            // edges of same color.
            boolean someone_removed = false;
            for (int x : vertices)
            {

                // note down different color values
                // for each vertex
                HashSet<Integer> values = new HashSet<>();
                for (int y : vertices)
                {
                    if (y != x)
                    {
                        values.add(C[x][y]);
                    }
                }

                // if only one color is found
                // erase that vertex (bad vertex)
                if (values.size() == 1)
                {
                    vertices.remove(x);
                    someone_removed = true;
                    break;
                }
            }

            // If no vertex was removed in the
            // above loop.
            if (!someone_removed)
            {
                break;
            }
        }

        return (vertices.size());
    }

    // Driver code
    public static void main(String[] args)
    {
        int C[][] = {{0, 9, 2, 4, 7, 8},
        {9, 0, 9, 9, 7, 9},
        {2, 9, 0, 3, 7, 6},
        {4, 9, 3, 0, 7, 1},
        {7, 7, 7, 7, 0, 7},
        {8, 9, 6, 1, 7, 0}
        };
        System.out.println(subsetGraph(C));
    }
}

// This code has been contributed by 29AjayKumar

Python3

# Python3 program to find size of subset
# of graph vertex such that each vertex
# has more than 1 color edges

# function to calculate max subset size
def subsetGraph(C):
    global N

    # set for number of vertices
    vertices = set()
    for i in range(N):
        vertices.add(i)

    # loop for deletion of vertex from set
    while (len(vertices) != 0):

        # if subset has only 1 vertex return 0
        if (len(vertices) == 1):
            return 1

        # for each vertex iterate and keep removing
        # a vertex while we find a vertex with all
        # edges of same color.
        someone_removed = False
        for x in vertices:

            # note down different color values
            # for each vertex
            values = set()
            for y in vertices:
                if (y != x):
                    values.add(C[x][y])

            # if only one color is found
            # erase that vertex (bad vertex)
            if (len(values) == 1):
                vertices.remove(x)
                someone_removed = True
                break

        # If no vertex was removed in the
        # above loop.
        if (not someone_removed):
            break

    return len(vertices)

# Driver Code

# Number of vertices
N = 6
C = [[0, 9, 2, 4, 7, 8],
     [9, 0, 9, 9, 7, 9],
     [2, 9, 0, 3, 7, 6],
     [4, 9, 3, 0, 7, 1],
     [7, 7, 7, 7, 0, 7],
     [8, 9, 6, 1, 7, 0]]
print(subsetGraph(C))

# This code is contributed by PranchalK

C#

// C# program to find size of
// subset of graph vertex such that
// each vertex has more than 1 color edges
using System;
using System.Collections.Generic;

class GFG
{

    // Number of vertices
    static int N = 6;

    // function to calculate max subset size
    static int subsetGraph(int [,]C)
    {
        // set for number of vertices
        HashSet<int> vertices = new HashSet<int>();
        for (int i = 0; i < N; ++i)
        {
            vertices.Add(i);
        }

        // loop for deletion of vertex from set
        while (vertices.Count != 0)
        {

            // if subset has only 1 vertex return 0
            if (vertices.Count == 1)
            {
                return 1;
            }

            // for each vertex iterate and keep removing
            // a vertex while we find a vertex with all
            // edges of same color.
            Boolean someone_removed = false;
            foreach (int x in vertices)
            {

                // note down different color values
                // for each vertex
                HashSet<int> values = new HashSet<int>();
                foreach (int y in vertices)
                {
                    if (y != x)
                    {
                        values.Add(C[x, y]);
                    }
                }

                // if only one color is found
                // erase that vertex (bad vertex)
                if (values.Count == 1)
                {
                    vertices.Remove(x);
                    someone_removed = true;
                    break;
                }
            }

            // If no vertex was removed in the
            // above loop.
            if (!someone_removed)
            {
                break;
            }
        }

        return (vertices.Count);
    }

    // Driver code
    public static void Main(String[] args)
    {
        int [,]C = {{0, 9, 2, 4, 7, 8},
                    {9, 0, 9, 9, 7, 9},
                    {2, 9, 0, 3, 7, 6},
                    {4, 9, 3, 0, 7, 1},
                    {7, 7, 7, 7, 0, 7},
                    {8, 9, 6, 1, 7, 0}};
        Console.WriteLine(subsetGraph(C));
    }
}

// This code is contributed by Rajput-Ji

Javascript

<script>

// Javascript program to find size of
// subset of graph vertex such that
// each vertex has more than 1 color edges

// Number of vertices
let N = 6;

// Function to calculate max subset size
function subsetGraph(C)
{

    // Set for number of vertices
    let vertices = new Set();
    for(let i = 0; i < N; ++i)
    {
        vertices.add(i);
    }

    // Loop for deletion of vertex from set
    while (vertices.size != 0)
    {

        // If subset has only 1 vertex return 0
        if (vertices.size == 1)
        {
            return 1;
        }

        // For each vertex iterate and keep removing
        // a vertex while we find a vertex with all
        // edges of same color.
        let someone_removed = false;

        for(let x of vertices.values())
        {

            // Note down different color values
            // for each vertex
            let values = new Set();
            for(let y of vertices.values())
            {
                if (y != x)
                {
                    values.add(C[x][y]);
                }
            }

            // If only one color is found
            // erase that vertex (bad vertex)
            if (values.size == 1)
            {
                vertices.delete(x);
                someone_removed = true;
                break;
            }
        }

        // If no vertex was removed in the
        // above loop.
        if (!someone_removed)
        {
            break;
        }
    }
    return (vertices.size);
}

// Driver code
let C = [ [ 0, 9, 2, 4, 7, 8 ],
          [ 9, 0, 9, 9, 7, 9 ],
          [ 2, 9, 0, 3, 7, 6 ],
          [ 4, 9, 3, 0, 7, 1 ],
          [ 7, 7, 7, 7, 0, 7 ],
          [ 8, 9, 6, 1, 7, 0 ] ];

document.write(subsetGraph(C));

// This code is contributed by rag2127

</script>

Output

4

This article is contributed by Shivam Pradhan . If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.