Largest sub-array whose all elements are perfect squares
Last Updated :
08 Sep, 2022
Given an array 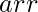 of integer elements, the task is to find the length of the largest sub-array of
of integer elements, the task is to find the length of the largest sub-array of 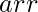 such that all the elements of the sub-array are perfect squares.
such that all the elements of the sub-array are perfect squares.
Examples:
Input: arr[] = {1, 7, 36, 4, 49, 2, 4}
Output: 3
Maximum length sub-array with all elements as perfect squares is {36, 4, 49}
Input: arr[] = {25, 100, 2, 3, 9, 1}
Output: 2
Possible sub-array is {25, 100}
Approach:
- Traverse the array from left to right. Initialize a max_length and current_length variable with 0.
- Take an integer and a float variable and for every element of the array store it’s square root in both these variables.
- If both the variables are equal i.e. the current element is a perfect square then increment current_length variable and continue. Otherwise, set current_length = 0.
- At each step, assign max_length as max_length = max(current_length, max_length).
- Print the value of max_length in the end.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int contiguousPerfectSquare(int arr[], int n)
{
int a;
float b;
int current_length = 0;
int max_length = 0;
for (int i = 0; i < n; i++) {
b = sqrt(arr[i]);
a = b;
if (a == b)
current_length++;
else
current_length = 0;
max_length = max(max_length, current_length);
}
return max_length;
}
int main()
{
int arr[] = { 9, 75, 4, 64, 121, 25 };
int n = sizeof(arr) / sizeof(arr[0]);
cout << contiguousPerfectSquare(arr, n);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int contiguousPerfectSquare(int []arr, int n)
{
int a;
float b;
int current_length = 0;
int max_length = 0;
for (int i = 0; i < n; i++) {
b = (float)Math.sqrt(arr[i]);
a = (int)b;
if (a == b)
current_length++;
else
current_length = 0;
max_length = Math.max(max_length, current_length);
}
return max_length;
}
public static void main (String[] args) {
int arr[] = { 9, 75, 4, 64, 121, 25 };
int n = arr.length;
System.out.print(contiguousPerfectSquare(arr, n));
}
}
|
Python3
from math import sqrt
def contiguousPerfectSquare(arr, n):
current_length = 0
max_length = 0
for i in range(0, n, 1):
b = sqrt(arr[i])
a = int(b)
if (a == b):
current_length += 1
else:
current_length = 0
max_length = max(max_length,
current_length)
return max_length
if __name__ == '__main__':
arr = [9, 75, 4, 64, 121, 25]
n = len(arr)
print(contiguousPerfectSquare(arr, n))
|
C#
using System;
class GFG {
static int contiguousPerfectSquare(int []arr, int n)
{
int a;
float b;
int current_length = 0;
int max_length = 0;
for (int i = 0; i < n; i++) {
b = (float)Math.Sqrt(arr[i]);
a = (int)b;
if (a == b)
current_length++;
else
current_length = 0;
max_length = Math.Max(max_length, current_length);
}
return max_length;
}
public static void Main () {
int []arr = { 9, 75, 4, 64, 121, 25 };
int n = arr.Length;
Console.WriteLine(contiguousPerfectSquare(arr, n));
}
}
|
PHP
<?php
function contiguousPerfectSquare($arr, $n)
{
$current_length = 0;
$max_length = 0;
for ($i = 0; $i < $n; $i++)
{
$b = (float)sqrt($arr[$i]);
$a = (int)$b;
if ($a == $b)
$current_length = $current_length + 1;
else
$current_length = 0;
$max_length = max($max_length,
$current_length);
}
return $max_length;
}
$arr = array(9, 75, 4, 64, 121, 25);
$n = sizeof($arr);
echo contiguousPerfectSquare($arr, $n);
?>
|
Javascript
<script>
function contiguousPerfectSquare(arr, n)
{
var a;
var b;
var current_length = 0;
var max_length = 0;
for (var i = 0; i < n; i++) {
b = (Math.sqrt(arr[i]));
a = parseInt(b);
if (a == b)
current_length++;
else
current_length = 0;
max_length = Math.max(max_length, current_length);
}
return max_length;
}
var arr = [9, 75, 4, 64, 121, 25 ];
var n = arr.length;
document.write( contiguousPerfectSquare(arr, n));
</script>
|
Complexity Analysis:
- Time Complexity: O(nlogn)
- Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...