Largest square which can be formed using given rectangular blocks

Given an array arr[] of positive integers where each element of the array represents the length of the rectangular blocks. The task is to find the largest length of the square which can be formed using the rectangular blocks.

Examples:

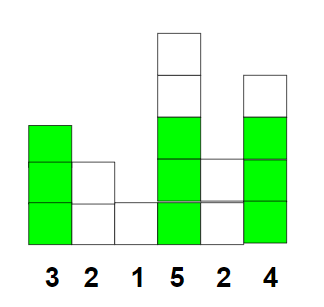
Input: arr[] = {3, 2, 1, 5, 2, 4} 
Output: 3 
Explanation:
Using rectangular block of length 3, 5 and 4, square of side length 3 can be constructed as shown below: 

Input: arr[] = {1, 2, 3} 
Output: 2 

Approach:

1. Sort the given array in decreasing order.
2. Initialise maximum sidelength(say maxLength) as 0.
3. Traverse the array arr[] and if arr[i] > maxLength then increment the maxLength and check this condition for next iteration.
4. If the above condition doesn’t satisfy then break the loop and print the maxLength.

Below is the implementation of the above approach: 

C++

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;

// Function to find maximum side
// length of square
void maxSide(int a[], int n)
{
    int sideLength = 0;

    // Sort array in asc order
    sort(a, a + n);

    // Traverse array in desc order
    for (int i = n - 1; i >= 0; i--) {

        if (a[i] > sideLength) {
            sideLength++;
        }
        else {
            break;
        }
    }
    cout << sideLength << endl;
}

// Driver Code
int main()
{
    int N = 6;

    // Given array arr[]
    int arr[] = { 3, 2, 1, 5, 2, 4 };

    // Function Call
    maxSide(arr, N);
    return 0;
}

Java

// Java program for the above approach
import java.util.Arrays;

class GFG{

// Function to find maximum side
// length of square
static void maxSide(int a[], int n)
{
    int sideLength = 0;

    // Sort array in asc order
    Arrays.sort(a);

    // Traverse array in desc order
    for(int i = n - 1; i >= 0; i--)
    {
       if (a[i] > sideLength)
       {
           sideLength++;
       }
       else
       {
           break;
       }
    }
    System.out.println(sideLength);
}

// Driver code
public static void main (String[] args)
{
    int N = 6;

    // Given array arr[]
    int arr[] = new int[]{ 3, 2, 1,
                           5, 2, 4 };

    // Function Call
    maxSide(arr, N);
}
}

// This code is contributed by Pratima Pandey

Python3

# Python3 program for the above approach

# Function to find maximum side
# length of square
def maxSide(a, n):

    sideLength = 0

    # Sort array in asc order
    a.sort

    # Traverse array in desc order
    for i in range(n - 1, -1, -1):
        if (a[i] > sideLength):
            sideLength += 1
        else:
            break

    print(sideLength)

# Driver code
N = 6

# Given array arr[]
arr = [ 3, 2, 1, 5, 2, 4 ]

# Function Call
maxSide(arr, N)

# This code is contributed by divyeshrabadiya07

C#

// C# program for the above approach
using System;
class GFG{

// Function to find maximum side
// length of square
static void maxSide(int []a, int n)
{
    int sideLength = 0;

    // Sort array in asc order
    Array.Sort(a);

    // Traverse array in desc order
    for(int i = n - 1; i >= 0; i--)
    {
        if (a[i] > sideLength)
        {
            sideLength++;
        }
        else
        {
            break;
        }
    }
    Console.Write(sideLength);
}

// Driver code
public static void Main()
{
    int N = 6;

    // Given array arr[]
    int []arr = new int[]{ 3, 2, 1,
                           5, 2, 4 };

    // Function Call
    maxSide(arr, N);
}
}

// This code is contributed by Code_Mech

Javascript

<script>
// Javascript program for the above approach
    // Function to find maximum side
    // length of square
    function maxSide( a, n) {
        let sideLength = 0;

        // Sort array in asc order
        a.sort();

        // Traverse array in desc order
        for ( i = n - 1; i >= 0; i--) {
            if (a[i] > sideLength) {
                sideLength++;
            } else {
                break;
            }
        }
        document.write(sideLength);
    }

    // Driver code

        let N = 6;

        // Given array arr
        let arr = [3, 2, 1, 5, 2, 4 ];

        // Function Call
        maxSide(arr, N);


// This code contributed by aashish1995
</script>

Output

3

Time Complexity: O(N*log N) 
Auxiliary Space: O(1)

Approach: Binary Search

Idea: Start by setting the low and high values as 1 and the sum of all elements in the array, respectively. Then, check if a square of mid-length can be formed using the given blocks. If yes, update the low value as mid+1. Otherwise, update the high value as mid-1.

Below is the implementation of the above approach: 

C++

// C++ program of the above approach

#include <iostream>
#include <vector>
using namespace std;

// Function to check if a square of length k can be formed
// using the given blocks
bool isSquarePossible(vector<int>& arr, int k)
{
    int count = 0;
    for (int i = 0; i < arr.size(); i++) {
        count += arr[i] / k;
        if (count >= k)
            return true;
    }
    return false;
}

int largestSquareLength(vector<int>& arr)
{
    int n = arr.size();
    int low = 1;
    int high = 0;
    // Calculate the total sum of all block lengths in the
    // array
    for (int i = 0; i < n; i++)
        high += arr[i];
    int result = 0;

    // Binary search loop
    while (low <= high) {
        int mid = low + (high - low) / 2;
        if (isSquarePossible(arr, mid)) {
            result = mid;
            low = mid + 1;
        }
        else {
            high = mid - 1;
        }
    }
    // Return the largest square length found
    return result;
}

// Driver Code
int main()
{
    vector<int> arr = { 1, 2, 3 };
    int largestSquare = largestSquareLength(arr);
    cout << largestSquare << endl;

    return 0;
}

Java

import java.util.ArrayList;
import java.util.List;

class GFG {
    // Function to check if it's possible to form a square
  // with side length 'k' using elements in 'arr'
    public static boolean isSquarePossible(List<Integer> arr, int k) {
        int count = 0;
        for (int i = 0; i < arr.size(); i++) {
            // Count the number of squares that can be formed
          // with each element in 'arr'
            count += arr.get(i) / k;
            // If the count is greater than or equal to 'k',
          // it means we can form a square with side length 'k'
            if (count >= k)
                return true;
        }
        // If no square of side length 'k' can be formed, return false
        return false;
    }

    // Function to find the largest possible side length of a
  // square that can be formed using elements in 'arr'
    public static int largestSquareLength(List<Integer> arr) {
        int n = arr.size();
        int low = 1;
        int high = 0;
        for (int i = 0; i < n; i++)
            high += arr.get(i);
        int result = 0;

        // Binary search to find the largest possible side
      // length of the square
        while (low <= high) {
            int mid = low + (high - low) / 2;
            // Check if it's possible to form a square with
          // side length 'mid'
            if (isSquarePossible(arr, mid)) {
                result = mid;
                // If it's possible to form a square with side
              // length 'mid', try larger side lengths
                low = mid + 1;
            } else {
                // If it's not possible to form a square with side
              // length 'mid', try smaller side lengths
                high = mid - 1;
            }
        }

        // Return the largest possible side length of the square
      // that can be formed using elements in 'arr'
        return result;
    }

    public static void main(String[] args) {
        List<Integer> arr = new ArrayList<>();
        arr.add(1);
        arr.add(2);
        arr.add(3);
        // Find the largest possible side length of a square that can be formed using elements in 'arr'
        int largestSquare = largestSquareLength(arr);
        System.out.println(largestSquare); // Print the result
    }
}

Python3

# Python code of the above mentioned approach

# Function to check if a square of length k is possible
# by using the given blocks
def is_square_possible(arr, k):
    count = 0
    for i in range(len(arr)):
        count += arr[i] // k
        if count >= k:
            return True
    return False

# Function to calculate the length of the
# largest square
def largest_square_length(arr):
    n = len(arr)
    low = 1
    high = 0

    # Finding the total sum of
    # the all blocks of the arryas
    for i in range(n):
        high += arr[i]
    result = 0

    # Doing Binary Search
    while low <= high:
        mid = low + (high - low) // 2
        if is_square_possible(arr, mid):
            result = mid
            low = mid + 1
        else:
            high = mid - 1

    # Returning the final Result
    return result

# Driver Code
arr = [1, 2, 3]
largest_square = largest_square_length(arr)
print(largest_square)

C#

using System;
using System.Collections.Generic;

public class GFG
{
    // Function to check if a square of length k can be formed
    // using the given blocks
    public static bool IsSquarePossible(List<int> arr, int k)
    {
        int count = 0;
        foreach (int block in arr)
        {
            count += block / k;
            if (count >= k)
                return true;
        }
        return false;
    }

    public static int LargestSquareLength(List<int> arr)
    {
        int n = arr.Count;
        int low = 1;
        int high = 0;
        // Calculate the total sum of all block lengths in the array
        foreach (int block in arr)
            high += block;
        int result = 0;

        // Binary search loop
        while (low <= high)
        {
            int mid = low + (high - low) / 2;
            if (IsSquarePossible(arr, mid))
            {
                result = mid;
                low = mid + 1;
            }
            else
            {
                high = mid - 1;
            }
        }
        // Return the largest square length found
        return result;
    }

    public static void Main(string[] args)
    {
        List<int> arr = new List<int> { 1, 2, 3 };
        int largestSquare = LargestSquareLength(arr);
        Console.WriteLine(largestSquare);
    }
}

Javascript

// Function to check if a square of length k can be formed
// using the given blocks
function isSquarePossible(arr, k) {
    let count = 0;
    // Iterate through each block length in the array
    for (let block of arr) {
        // Calculate how many blocks of size k can be formed from the current block
        count += Math.floor(block / k);
        // If we have enough blocks to form a square of size k, return true
        if (count >= k) {
            return true;
        }
    }
    // If we couldn't form a square of size k using the given blocks, return false
    return false;
}

// Function to find the largest square length that can be formed
function largestSquareLength(arr) {
    const n = arr.length;
    let low = 1;
    let high = 0;
    // Calculate the total sum of all block lengths in the array
    for (let block of arr) {
        high += block;
    }
    let result = 0;

    // Binary search loop to find the largest possible square length
    while (low <= high) {
        const mid = Math.floor(low + (high - low) / 2);
        if (isSquarePossible(arr, mid)) {
            // If a square of size mid is possible, update result and search higher
            result = mid;
            low = mid + 1;
        } else {
            // If a square of size mid is not possible, search lower
            high = mid - 1;
        }
    }
    // Return the largest square length found
    return result;
}

// Example array of block lengths
const arr = [1, 2, 3];
// Find and print the largest square length that can be formed
const largestSquare = largestSquareLength(arr);
console.log(largestSquare);

Output

2

Time Complexity: O(n log M), where n is the number of elements in the input array and M is the sum of all elements in the array.
Auxiliary Space: O(1)