Largest right circular cylinder within a frustum
Last Updated :
20 Aug, 2022
Given a frustum of height 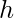 , top-radius
, top-radius 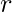 & base-radius
& base-radius 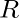 . The task is to find the volume of biggest right circular cylinder that can be inscribed within it.
. The task is to find the volume of biggest right circular cylinder that can be inscribed within it.
Examples:
Input : r = 5, R = 10, h = 4
Output : 314
Input : r = 7, R = 11, h = 6
Output : 923.16

Approach:
Let:
- The height of the cylinder = h1
- Radius of the cylinder = r1
From the figure it is clear that:
- Height of the cylinder = Height of frustum
- Radius of the cylinder = Rop-radius of the frustum
So,
h1 = h
r1 = r
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
float cyl(float r, float R, float h)
{
if (h < 0 && r < 0 && R < 0)
return -1;
float r1 = r;
float h1 = h;
float V = 3.14 * pow(r1, 2) * h1;
return V;
}
int main()
{
float r = 7, R = 11, h = 6;
cout << cyl(r, R, h) << endl;
return 0;
}
|
Java
import java.io.*;
class GFG {
static float cyl(float r, float R, float h)
{
if (h < 0 && r < 0 && R < 0)
return -1;
float r1 = r;
float h1 = h;
float V = (float)(3.14 * Math.pow(r1, 2) * h1);
return V;
}
public static void main (String[] args) {
float r = 7, R = 11, h = 6;
System.out.print( cyl(r, R, h));
}
}
|
Python3
def cyl(r, R, h) :
if (h < 0 and r < 0 and R < 0) :
return -1
r1 = r
h1 = h
V = 3.14 * pow(r1, 2) * h1
return round(V,2)
if __name__ == "__main__" :
r, R, h = 7, 11, 6
print(cyl(r, R, h))
|
C#
using System;
class GFG {
static float cyl(float r, float R, float h)
{
if (h < 0 && r < 0 && R < 0)
return -1;
float r1 = r;
float h1 = h;
float V = (float)(3.14 * Math.Pow(r1, 2) * h1);
return V;
}
public static void Main () {
float r = 7, R = 11, h = 6;
Console.WriteLine( cyl(r, R, h));
}
}
|
PHP
<?php
function cyl($r, $R, $h)
{
if ($h < 0 && $r < 0 && $R < 0)
return -1;
$r1 = $r;
$h1 = $h;
$V = (3.14 * pow($r1, 2) * $h1);
return $V;
}
$r = 7; $R = 11; $h = 6;
echo cyl($r, $R, $h);
|
Javascript
<script>
function cyl(r , R , h)
{
if (h < 0 && r < 0 && R < 0)
return -1;
var r1 = r;
var h1 = h;
var V = (3.14 * Math.pow(r1, 2) * h1);
return V;
}
var r = 7, R = 11, h = 6;
document.write( cyl(r, R, h).toFixed(5));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...