Largest right circular cylinder that can be inscribed within a cone

Given a right circular cylinder which is inscribed in a cone of height h and base radius r. The task is to find the largest possible volume of the cylinder.
Examples:

Input: r = 4, h = 8
Output: 119.087

Input: r = 5, h = 9
Output: 209.333

Approach: The volume of a cylinder is V = πr^2h
In this problem, first derive an equation for volume using similar triangles in terms of the height and radius of the cone. Once we have the modified the volume equation, we’ll take the derivative of the volume and solve for the largest value. 
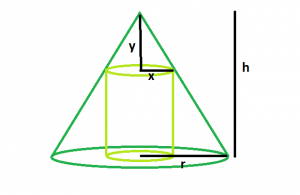
Let x be the radius of the cylinder and y be the distance from the top of the cone to the top of the inscribed cylinder. Therefore, the height of the cylinder is h – y
The volume of the inscribed cylinder is V = πx^2(h-y). 
We use the method of similar ratios to find a relationship between the height and radius, h-y and x. 
y/x = h/r 
y = hx/r
Substitute the equation for y into the equation for volume, V. 

V = πx^2(h-y) 
V = πx^2(h-hx/r) 
V = πx^2h – πx^3h/r
now, dV/dx = d(πx^2h – πx^3h/r)/dx
and setting dV/dx = 0
we get, x = 0, 2r/3
So, x = 2r/3
and, y = 2h/3
So, V = π8r^2h/27

Below is the implementation of the above approach:

C++

// C++ Program to find the biggest
// right circular cylinder that can
// be fit within a right circular cone

#include <bits/stdc++.h>
using namespace std;

// Function to find the biggest right circular cylinder
float cyl(float r, float h)
{

    // radius and height cannot be negative
    if (r < 0 && h < 0)
        return -1;

    // radius of right circular cylinder
    float R = (2 * r) / 3;

    // height of right circular cylinder
    float H = (2 * h) / 3;

    // volume of right circular cylinder
    float V = 3.14 * pow(R, 2) * H;

    return V;
}

// Driver code
int main()
{
    float r = 4, h = 8;
    cout << cyl(r, h) << endl;

    return 0;
}

Java

// Java Program to find the biggest
// right circular cylinder that can
// be fit within a right circular cone

import java.io.*;

class GFG {
// Function to find the biggest right circular cylinder
static double cyl(double r, double h)
{

    // radius and height cannot be negative
    if (r < 0 && h < 0)
        return -1;

    // radius of right circular cylinder
    double R = (2 * r) / 3;

    // height of right circular cylinder
    double H = (2 * h) / 3;

    // volume of right circular cylinder
    double V = 3.14 * Math.pow(R, 2) * H;

    return V;
}

// Driver code

    public static void main (String[] args) {

    double r = 4, h = 8;
    System.out.println (cyl(r, h));
    }
//This code is contributed by ajit
}

Python 3

# Python 3 Program to find the biggest
# right circular cylinder that can
# be fit within a right circular cone
import math

# Function to find the biggest
# right circular cylinder
def cyl(r, h):

    # radius and height cannot
    # be negative
    if (r < 0 and h < 0):
        return -1

    # radius of right circular cylinder
    R = (2 * r) / 3

    # height of right circular cylinder
    H = (2 * h) / 3

    # volume of right circular cylinder
    V = 3.14 * math.pow(R, 2) * H

    return V

# Driver code
r = 4; h = 8;
print(cyl(r, h), "\n")

# This code is contributed
# by Akanksha Rai

C#

// C# Program to find the biggest
// right circular cylinder that
// can be fit within a right circular cone
using System;

class GFG
{

// Function to find the biggest
// right circular cylinder
static double cyl(double r, double h)
{

    // radius and height cannot
    // be negative
    if (r < 0 && h < 0)
        return -1;

    // radius of right circular cylinder
    double R = (2 * r) / 3;

    // height of right circular cylinder
    double H = (2 * h) / 3;

    // volume of right circular cylinder
    double V = 3.14 * Math.Pow(R, 2) * H;

    return V;
}

// Driver code
static public void Main ()
{
    double r = 4, h = 8;
    Console.WriteLine(cyl(r, h));
}
}

// This code is contributed by jit_t

PHP

<?php
// PHP Program to find the biggest
// right circular cylinder that can
// be fit within a right circular cone

// Function to find the biggest
// right circular cylinder
function cyl($r, $h)
{

    // radius and height cannot
    // be negative
    if ($r < 0 && $h < 0)
        return -1;

    // radius of right circular cylinder
    $R = (int)(2 * $r) / 3;

    // height of right circular cylinder
    $H = (int)(2 * $h) / 3;

    // volume of right circular cylinder
    $V = 3.14 * pow($R, 2) * $H;

    return $V;
}

// Driver code
$r = 4;
$h = 8;
echo cyl($r, $h);

// This code is contributed by ajit
?>

Javascript

<script>
// javascript Program to find the biggest
// right circular cylinder that can
// be fit within a right circular cone

// Function to find the biggest right circular cylinder
function cyl(r , h)
{

    // radius and height cannot be negative
    if (r < 0 && h < 0)
        return -1;

    // radius of right circular cylinder
    var R = (2 * r) / 3;

    // height of right circular cylinder
    var H = (2 * h) / 3;

    // volume of right circular cylinder
    var V = 3.14 * Math.pow(R, 2) * H;

    return V;
}

// Driver code

var r = 4, h = 8;
document.write(cyl(r, h).toFixed(5));

// This code is contributed by shikhasingrajput
</script>

Output:

119.087

Time Complexity: O(1)

Auxiliary Space: O(1)