Largest perfect square number in an Array

Given an array of n integers. The task is to find the largest number which is a perfect square. Print -1 if there is no number that is perfect square.
Examples: 

Input : arr[] = {16, 20, 25, 2, 3, 10} 
Output : 25
Explanation: 25 is the largest number 
that is a perfect square. 

Input : arr[] = {36, 64, 10, 16, 29, 25| 
Output : 64

A Simple Solution is to sort the elements and sort the n numbers and start checking from back for a perfect square number using sqrt() function. The first number from the end which is a perfect square number is our answer. The complexity of sorting is O(n log n) and of sqrt() function is log n, so at the worst case the complexity is O(n log n).
An Efficient Solution is to iterate for all the elements in O(n) and compare every time with the maximum element, and store the maximum of all perfect squares. 
Below is the implementation of the above approach:

C++

// CPP program to find the largest perfect
// square number among n numbers

#include<iostream>
#include<math.h>
using namespace std;

// Function to check if a number
// is perfect square number or not
bool checkPerfectSquare(double n)
{
    // takes the sqrt of the number
    double d = sqrt(n);

    // checks if it is a perfect
    // square number
    if (d * d == n)
        return true;

    return false;
}

// Function to find the largest perfect
// square number in the array
int largestPerfectSquareNumber(int a[], double n)
{
    // stores the maximum of all
    // perfect square numbers
    int maxi = -1;

    // Traverse all elements in the array
    for (int i = 0; i < n; i++) {

        // store the maximum if current
        // element is a perfect square
        if (checkPerfectSquare(a[i]))
            maxi = max(a[i], maxi);
    }

    return maxi;
}

// Driver Code
int main()
{
    int a[] = { 16, 20, 25, 2, 3, 10 };

    double n = sizeof(a) / sizeof(a[0]);

    cout << largestPerfectSquareNumber(a, n);

    return 0;
}

C

// C program to find the largest perfect
// square number among n numbers
#include <stdio.h>
#include <stdbool.h>
#include <math.h>

int max(int a,int b)
{
  int max = a;
  if(max < b)
    max = b;
  return max;
}

// Function to check if a number
// is perfect square number or not
bool checkPerfectSquare(double n)
{
    // takes the sqrt of the number
    double d = sqrt(n);

    // checks if it is a perfect
    // square number
    if (d * d == n)
        return true;

    return false;
}

// Function to find the largest perfect
// square number in the array
int largestPerfectSquareNumber(int a[], double n)
{
    // stores the maximum of all
    // perfect square numbers
    int maxi = -1;

    // Traverse all elements in the array
    for (int i = 0; i < n; i++) {

        // store the maximum if current
        // element is a perfect square
        if (checkPerfectSquare(a[i]))
            maxi = max(a[i], maxi);
    }

    return maxi;
}

// Driver Code
int main()
{
    int a[] = { 16, 20, 25, 2, 3, 10 };

    double n = sizeof(a) / sizeof(a[0]);

    printf("%d",largestPerfectSquareNumber(a, n));

    return 0;
}

// This code is contributed by kothavvsaakash.

Java

// Java program to find the largest perfect
// square number among n numbers
import java.lang.Math;
import java.io.*;

class GFG {


// Function to check if a number
// is perfect square number or not
static boolean checkPerfectSquare(double n)
{
    // takes the sqrt of the number
    double d = Math.sqrt(n);

    // checks if it is a perfect
    // square number
    if (d * d == n)
        return true;

    return false;
}

// Function to find the largest perfect
// square number in the array
static int largestPerfectSquareNumber(int a[], double n)
{
    // stores the maximum of all
    // perfect square numbers
    int maxi = -1;

    // Traverse all elements in the array
    for (int i = 0; i < n; i++) {

        // store the maximum if current
        // element is a perfect square
        if (checkPerfectSquare(a[i]))
            maxi = Math.max(a[i], maxi);
    }

    return maxi;
}

// Driver Code


    public static void main (String[] args) {
            int []a = { 16, 20, 25, 2, 3, 10 };

    double n = a.length;

    System.out.println( largestPerfectSquareNumber(a, n));

    }
}
// This code is contributed
// by inder_verma..

Python3

# Python3 program to find the largest perfect
# square number among n numbers

# from math lib import sqrt()
from math import sqrt

# Function to check if a number
# is perfect square number or not
def checkPerfectSquare(n) :

    # takes the sqrt of the number
    d = sqrt(n)

    # checks if it is a perfect
    # square number
    if d * d == n :
        return True

    return False


# Function to find the largest perfect
# square number in the array
def largestPerfectSquareNumber(a, n) :

    # stores the maximum of all
    # perfect square numbers
    maxi = -1

    # Traverse all elements in the array
    for i in range(n) :

        # store the maximum if current
        # element is a perfect square
        if(checkPerfectSquare(a[i])) :
            maxi = max(a[i], maxi)

    return maxi


# Driver code
if __name__ == "__main__" :

    a = [16, 20, 25, 2, 3, 10 ]
    n = len(a)

    print(largestPerfectSquareNumber(a, n))

# This code is contributed by Ryuga

C#

// C# program to find the largest perfect
// square number among n numbers
using System;
class GFG {


// Function to check if a number
// is perfect square number or not
static bool checkPerfectSquare(double n)
{
    // takes the sqrt of the number
    double d = Math.Sqrt(n);

    // checks if it is a perfect
    // square number
    if (d * d == n)
        return true;

    return false;
}

// Function to find the largest perfect
// square number in the array
static int largestPerfectSquareNumber(int []a, double n)
{
    // stores the maximum of all
    // perfect square numbers
    int maxi = -1;

    // Traverse all elements in the array
    for (int i = 0; i < n; i++) {

        // store the maximum if current
        // element is a perfect square
        if (checkPerfectSquare(a[i]))
            maxi = Math.Max(a[i], maxi);
    }

    return maxi;
}

// Driver Code


    public static void Main () {
            int []a = { 16, 20, 25, 2, 3, 10 };

    double n = a.Length;

    Console.WriteLine( largestPerfectSquareNumber(a, n));

    }
}
// This code is contributed
// by inder_verma..

PHP

<?php
// PHP program to find the largest perfect
// square number among n numbers

// Function to check if a number
// is perfect square number or not
function checkPerfectSquare($n)
{
    // takes the sqrt of the number
    $d = sqrt($n);

    // checks if it is a perfect
    // square number
    if ($d * $d == $n)
        return true;

    return false;
}

// Function to find the largest perfect
// square number in the array
function largestPerfectSquareNumber($a, $n)
{
    // stores the maximum of all
    // perfect square numbers
    $maxi = -1;

    // Traverse all elements in the array
    for ($i = 0; $i <$n; $i++)
    {

        // store the maximum if current
        // element is a perfect square
        if (checkPerfectSquare($a[$i]))
            $maxi = max($a[$i], $maxi);
    }

    return $maxi;
}

// Driver Code
$a = array( 16, 20, 25, 2, 3, 10 );

$n = count($a);

echo largestPerfectSquareNumber($a, $n);

// This code is contributed
// by inder_verma.
?>

Javascript

<script>

// Javascript program to find the largest perfect
// square number among n numbers

// Function to check if a number
// is perfect square number or not
function checkPerfectSquare(n)
{
    // takes the sqrt of the number
    let d = Math.sqrt(n);

    // checks if it is a perfect
    // square number
    if (d * d == n)
        return true;

    return false;
}

// Function to find the largest perfect
// square number in the array
function largestPerfectSquareNumber(a, n)
{
    // stores the maximum of all
    // perfect square numbers
    let maxi = -1;

    // Traverse all elements in the array
    for (let i = 0; i < n; i++)
    {

        // store the maximum if current
        // element is a perfect square
        if (checkPerfectSquare(a[i]))
            maxi = Math.max(a[i], maxi);
    }

    return maxi;
}

// Driver Code
let a = [ 16, 20, 25, 2, 3, 10 ];
let n = a.length;
document.write(largestPerfectSquareNumber(a, n));

// This code is contributed by souravmahato348.
</script>

Output:

25

Time Complexity : O()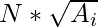
Auxiliary Space: O(1)