Largest factor of a given number which is a perfect square
Last Updated :
26 Oct, 2023
Given a number 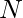 . The task is to find the largest factor of that number which is a perfect square.
. The task is to find the largest factor of that number which is a perfect square.
Examples:
Input : N = 420
Output : 4
Input : N = 100
Output : 100
A Simple Solution is to traverse all of the numbers in decreasing order from the given number down till 1 and if any of these numbers is a factor of the given number and is also a perfect square, print that number.
Time Complexity: O(N)
Better Solution : A better solution is to use prime factorization of the given number.
- First find all the prime factors of that number till sqrt(num).
- Take a variable, answer and initialize it to 1. It represents the largest square number which is also a factor of that number.
- Now, Check If any prime number occurs even number of times in the prime factorization of the given number, if yes then multiply the answer with that prime factor the number of times it occurs.
- Else, if it occurs odd number of times then multiply the answer with prime number (K – 1) times, K is the frequency of that prime factor in the prime factorization.
Below is the implementation of the above approach:
C++
#include <cmath>
#include <iostream>
using namespace std;
int largestSquareFactor(int num)
{
int answer = 1;
for (int i = 2; i < sqrt(num); ++i) {
int cnt = 0;
int j = i;
while (num % j == 0) {
cnt++;
j *= i;
}
if (cnt & 1) {
cnt--;
answer *= pow(i, cnt);
}
else {
answer *= pow(i, cnt);
}
}
return answer;
}
int main()
{
int N = 420;
cout << largestSquareFactor(N);
return 0;
}
|
Java
class GFG
{
static int largestSquareFactor(int num)
{
int answer = 1;
for (int i = 2; i < Math.sqrt(num); ++i) {
int cnt = 0;
int j = i;
while (num % j == 0) {
cnt++;
j *= i;
}
if ((cnt & 1)!=0) {
cnt--;
answer *= Math.pow(i, cnt);
}
else {
answer *= Math.pow(i, cnt);
}
}
return answer;
}
public static void main(String args[])
{
int N = 420;
System.out.println(largestSquareFactor(N));
}
}
|
Python 3
import math
def largestSquareFactor( num):
answer = 1
for i in range(2, int(math.sqrt(num))) :
cnt = 0
j = i
while (num % j == 0) :
cnt += 1
j *= i
if (cnt & 1) :
cnt -= 1
answer *= pow(i, cnt)
else :
answer *= pow(i, cnt)
return answer
if __name__ == "__main__":
N = 420
print(largestSquareFactor(N))
|
C#
using System;
class GFG
{
static double largestSquareFactor(double num)
{
double answer = 1;
for (int i = 2; i < Math.Sqrt(num); ++i)
{
int cnt = 0;
int j = i;
while (num % j == 0)
{
cnt++;
j *= i;
}
if ((cnt & 1) != 0)
{
cnt--;
answer *= Math.Pow(i, cnt);
}
else
{
answer *= Math.Pow(i, cnt);
}
}
return answer;
}
static public void Main ()
{
int N = 420;
Console.WriteLine(largestSquareFactor(N));
}
}
|
Javascript
<script>
function largestSquareFactor(num)
{
let answer = 1;
for (let i = 2; i < Math.sqrt(num); ++i)
{
let cnt = 0;
let j = i;
while (num % j == 0) {
cnt++;
j *= i;
}
if (cnt & 1)
{
cnt--;
answer *= Math.pow(i, cnt);
}
else {
answer *= Math.pow(i, cnt);
}
}
return answer;
}
let N = 420;
document.write(largestSquareFactor(N));
</script>
|
PHP
<?php
function largestSquareFactor($num)
{
$answer = 1;
for ($i = 2; $i < sqrt($num); ++$i)
{
$cnt = 0;
$j = $i;
while ($num % $j == 0)
{
$cnt++;
$j *= $i;
}
if ($cnt & 1)
{
$cnt--;
$answer *= pow($i, $cnt);
}
else
{
$answer *= pow($i, $cnt);
}
}
return $answer;
}
$N = 420;
echo largestSquareFactor($N);
?>
|
Time Complexity: O( sqrtn*logn)
Auxiliary Space: O(1)
Approach:
- Initialize a variable max_factor to 1, which will store the largest factor of the given number that is a perfect square.
- Iterate through all factors of the given number num using a for loop that goes from 1 to the square root of num.
- Check if i is a factor of num using the modulo operator. If it is, then find the corresponding factor num/i.
- Check if factor1 is a perfect square using the sqrt and floor functions from the cmath library. If it is, then update max_factor to be the maximum of max_factor and factor1.
- Check if factor2 is a perfect square using the sqrt and floor functions from the cmath library. If it is, then update max_factor to be the maximum of max_factor and factor2.
- Return the final value of max_factor.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int largestSquareFactor(int num)
{
int max_factor = 1;
for (int i = 1; i <= sqrt(num); i++) {
if (num % i == 0) {
int factor1 = i;
int factor2 = num / i;
if (sqrt(factor1) == floor(sqrt(factor1))) {
max_factor = max(max_factor, factor1);
}
if (sqrt(factor2) == floor(sqrt(factor2))) {
max_factor = max(max_factor, factor2);
}
}
}
return max_factor;
}
int main()
{
int N = 420;
cout << largestSquareFactor(N);
return 0;
}
|
Java
import java.util.*;
public class Main {
public static int largestSquareFactor(int num) {
int max_factor = 1;
for (int i = 1; i <= Math.sqrt(num); i++) {
if (num % i == 0) {
int factor1 = i;
int factor2 = num / i;
if (Math.sqrt(factor1) == Math.floor(Math.sqrt(factor1))) {
max_factor = Math.max(max_factor, factor1);
}
if (Math.sqrt(factor2) == Math.floor(Math.sqrt(factor2))) {
max_factor = Math.max(max_factor, factor2);
}
}
}
return max_factor;
}
public static void main(String[] args) {
int N = 420;
System.out.println(largestSquareFactor(N));
}
}
|
Python3
import math
def largestSquareFactor(num):
max_factor = 1
for i in range(1, int(math.sqrt(num))+1):
if num % i == 0:
factor1 = i
factor2 = num // i
if math.sqrt(factor1) == int(math.sqrt(factor1)):
max_factor = max(max_factor, factor1)
if math.sqrt(factor2) == int(math.sqrt(factor2)):
max_factor = max(max_factor, factor2)
return max_factor
N = 420
print(largestSquareFactor(N))
|
C#
using System;
public class Program
{
static int LargestSquareFactor(int num)
{
int maxFactor = 1;
for (int i = 1; i <= Math.Sqrt(num); i++)
{
if (num % i == 0)
{
int factor1 = i;
int factor2 = num / i;
if (Math.Sqrt(factor1) == Math.Floor(Math.Sqrt(factor1)))
{
maxFactor = Math.Max(maxFactor, factor1);
}
if (Math.Sqrt(factor2) == Math.Floor(Math.Sqrt(factor2)))
{
maxFactor = Math.Max(maxFactor, factor2);
}
}
}
return maxFactor;
}
public static void Main()
{
int N = 420;
Console.WriteLine(LargestSquareFactor(N));
}
}
|
Javascript
function largestSquareFactor(num) {
let max_factor = 1;
for (let i = 1; i <= Math.sqrt(num); i++) {
if (num % i == 0) {
let factor1 = i;
let factor2 = num / i;
if (Math.sqrt(factor1) == Math.floor(Math.sqrt(factor1))) {
max_factor = Math.max(max_factor, factor1);
}
if (Math.sqrt(factor2) == Math.floor(Math.sqrt(factor2))) {
max_factor = Math.max(max_factor, factor2);
}
}
}
return max_factor;
}
let N = 420;
console.log(largestSquareFactor(N));
|
Time Complexity: O(sqrt(N))
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...