Lamport One Time Signature Scheme
Last Updated :
31 May, 2021
Lamport One Time Signature is a method for constructing a digital signature and typically involved the use of a cryptographic hash function. As it is a one-time signature scheme, it can only be used to securely sign one message.
Suppose Alice wants to digitally sign her message to Bob, the process can be explained in 3 steps:
- Key Generation
- Signature Generation
- Signature Verification.
1. Key Generation:
- Alice first needs to create a Lamport key pair, a private key and a corresponding public key.
- In order to create the private key, a secure random number generator is used to generate 256 pairs of random numbers. Each number consists of 256 bits. Alice will store this private key securely. Remember that the private key is not meant to be shared with anyone.
- In order to create the public key, Alice hashes each of the 512 numbers of her private key. This will produce another 512 numbers, each consisting of 256 bits. This is the public key that will be shared with anyone.
In mathematical representation:
- let
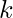 be a positive integer,
be a positive integer, 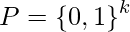 be the set of messages to be signed and
be the set of messages to be signed and 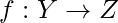 be a one way hash function.
be a one way hash function. - For
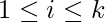 and
and 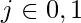 , Alice randomly chooses
, Alice randomly chooses 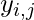 and applies the one way hash function to compute
and applies the one way hash function to compute 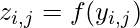 .
. - The private key and public key both consists of
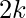 values,
values, 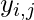 and
and 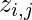 respectively.
respectively.
2. Signature Generation:
- Alice hashes her message using a 256-bit cryptographic hash function, eg SHA 256, to obtain a 256-bit digest.
- For each bit, depending on whether the bit value is 1 or 0, Alice will pick the corresponding number from the pair of numbers of her private key i.e. if the bit is 0, the first number is chosen, and if the bit is 1, the second number is chosen. This results in a sequence of 256 numbers which is her signature.

- Alice sends the message along with her signature to Bob.
In mathematical representation,
- let
 be the message Alice wants to sign.
be the message Alice wants to sign. - The signature is generated as
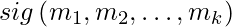 =
=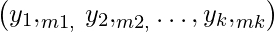 =
=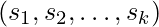 .
. - This signature is sent to Bob along with the message.
3. Signature Verification:
- Bob hashes the message using the same 256-bit cryptographic hash function, to obtain a 256-bit digest.
- For each bit, depending on whether the bit value is 1 or 0, Bob will pick the corresponding number from Alice’s public key i.e if the first bit of the message hash is 0, he picks the first hash in the first pair, and so on. This is done in the same manner as shown in the diagram above. This results in a sequence of 256 numbers.
- Bob hashes each of the numbers in Alice’s signature to obtain a 256-bit digest. If this matches the sequence of 256 numbers that Bob had previously picked out, the signature is valid.
In mathematical representation, Bob checks that 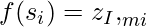 for all
for all 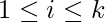
Note:It is important to understand that since Alice has publicly published half of a private key as her signature, her remaining private key cannot be used again and must be destroyed.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...