K’th smallest element in BST using O(1) Extra Space

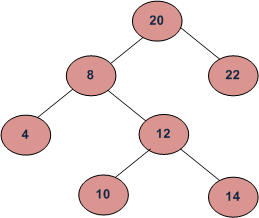
Given a Binary Search Tree (BST) and a positive integer k, find the k’th smallest element in the Binary Search Tree. 
For example, in the following BST, if k = 3, then output should be 10, and if k = 5, then output should be 14. 

We have discussed two methods in this post and one method in this post. All of the previous methods require extra space. How to find the k’th smallest element without extra space?

The idea is to use Morris Traversal. In this traversal, we first create links to Inorder successor and print the data using these links, and finally revert the changes to restore original tree. See this for more details.

Below is the implementation of the idea. 

C++

// C++ program to find k'th smallest element in BST
#include<bits/stdc++.h>
using namespace std;

// A BST node
struct Node
{
    int key;
    Node *left, *right;
};

// A function to find
int KSmallestUsingMorris(Node *root, int k)
{
    // Count to iterate over elements till we
    // get the kth smallest number
    int count = 0;

    int ksmall = INT_MIN; // store the Kth smallest
    Node *curr = root; // to store the current node

    while (curr != NULL)
    {
        // Like Morris traversal if current does
        // not have left child rather than printing
        // as we did in inorder, we will just
        // increment the count as the number will
        // be in an increasing order
        if (curr->left == NULL)
        {
            count++;

            // if count is equal to K then we found the
            // kth smallest, so store it in ksmall
            if (count==k)
                ksmall = curr->key;

            // go to current's right child
            curr = curr->right;
        }
        else
        {
            // we create links to Inorder Successor and
            // count using these links
            Node *pre = curr->left;
            while (pre->right != NULL && pre->right != curr)
                pre = pre->right;

            // building links
            if (pre->right==NULL)
            {
                //link made to Inorder Successor
                pre->right = curr;
                curr = curr->left;
            }

            // While breaking the links in so made temporary
            // threaded tree we will check for the K smallest
            // condition
            else
            {
                // Revert the changes made in if part (break link
                // from the Inorder Successor)
                pre->right = NULL;

                count++;

                // If count is equal to K then we found
                // the kth smallest and so store it in ksmall
                if (count==k)
                    ksmall = curr->key;

                curr = curr->right;
            }
        }
    }
    return ksmall; //return the found value
}

// A utility function to create a new BST node
Node *newNode(int item)
{
    Node *temp = new Node;
    temp->key = item;
    temp->left = temp->right = NULL;
    return temp;
}

/* A utility function to insert a new node with given key in BST */
Node* insert(Node* node, int key)
{
    /* If the tree is empty, return a new node */
    if (node == NULL) return newNode(key);

    /* Otherwise, recur down the tree */
    if (key < node->key)
        node->left  = insert(node->left, key);
    else if (key > node->key)
        node->right = insert(node->right, key);

    /* return the (unchanged) node pointer */
    return node;
}

// Driver Program to test above functions
int main()
{
    /* Let us create following BST
              50
           /     \
          30      70
         /  \    /  \
       20   40  60   80 */
    Node *root = NULL;
    root = insert(root, 50);
    insert(root, 30);
    insert(root, 20);
    insert(root, 40);
    insert(root, 70);
    insert(root, 60);
    insert(root, 80);

    for (int k=1; k<=7; k++)
       cout << KSmallestUsingMorris(root, k) << " ";

    return 0;
}

Java

// Java program to find k'th smallest element in BST
import java.util.*;
class GfG {

// A BST node
static class Node
{
    int key;
    Node left, right;
}

// A function to find
static int KSmallestUsingMorris(Node root, int k)
{
    // Count to iterate over elements till we
    // get the kth smallest number
    int count = 0;

    int ksmall = Integer.MIN_VALUE; // store the Kth smallest
    Node curr = root; // to store the current node

    while (curr != null)
    {
        // Like Morris traversal if current does
        // not have left child rather than printing
        // as we did in inorder, we will just
        // increment the count as the number will
        // be in an increasing order
        if (curr.left == null)
        {
            count++;

            // if count is equal to K then we found the
            // kth smallest, so store it in ksmall
            if (count==k)
                ksmall = curr.key;

            // go to current's right child
            curr = curr.right;
        }
        else
        {
            // we create links to Inorder Successor and
            // count using these links
            Node pre = curr.left;
            while (pre.right != null && pre.right != curr)
                pre = pre.right;

            // building links
            if (pre.right== null)
            {
                //link made to Inorder Successor
                pre.right = curr;
                curr = curr.left;
            }

            // While breaking the links in so made temporary
            // threaded tree we will check for the K smallest
            // condition
            else
            {
                // Revert the changes made in if part (break link
                // from the Inorder Successor)
                pre.right = null;

                count++;

                // If count is equal to K then we found
                // the kth smallest and so store it in ksmall
                if (count==k)
                    ksmall = curr.key;

                curr = curr.right;
            }
        }
    }
    return ksmall; //return the found value
}

// A utility function to create a new BST node
static Node newNode(int item)
{
    Node temp = new Node();
    temp.key = item;
    temp.left = null;
    temp.right = null;
    return temp;
}

/* A utility function to insert a new node with given key in BST */
static Node insert(Node node, int key)
{
    /* If the tree is empty, return a new node */
    if (node == null) return newNode(key);

    /* Otherwise, recur down the tree */
    if (key < node.key)
        node.left = insert(node.left, key);
    else if (key > node.key)
        node.right = insert(node.right, key);

    /* return the (unchanged) node pointer */
    return node;
}

// Driver Program to test above functions
public static void main(String[] args)
{
    /* Let us create following BST
            50
        /     \
        30     70
        / \ / \
    20 40 60 80 */
    Node root = null;
    root = insert(root, 50);
    insert(root, 30);
    insert(root, 20);
    insert(root, 40);
    insert(root, 70);
    insert(root, 60);
    insert(root, 80);

    for (int k=1; k<=7; k++)
    System.out.print(KSmallestUsingMorris(root, k) + " ");

}
}

Python3

# Python 3 program to find k'th
# smallest element in BST

# A BST node
class Node:

    # Constructor to create a new node
    def __init__(self, data):
        self.key = data
        self.left = None
        self.right = None

# A function to find
def KSmallestUsingMorris(root, k):

    # Count to iterate over elements
    # till we get the kth smallest number
    count = 0

    ksmall = -9999999999 # store the Kth smallest
    curr = root # to store the current node

    while curr != None:

        # Like Morris traversal if current does
        # not have left child rather than
        # printing as we did in inorder, we
        # will just increment the count as the
        # number will be in an increasing order
        if curr.left == None:
            count += 1

            # if count is equal to K then we
            # found the kth smallest, so store
            # it in ksmall
            if count == k:
                ksmall = curr.key

            # go to current's right child
            curr = curr.right
        else:

            # we create links to Inorder Successor
            # and count using these links
            pre = curr.left
            while (pre.right != None and
                   pre.right != curr):
                pre = pre.right

            # building links
            if pre.right == None:

                # link made to Inorder Successor
                pre.right = curr
                curr = curr.left

            # While breaking the links in so made
            # temporary threaded tree we will check
            # for the K smallest condition
            else:

                # Revert the changes made in if part
                # (break link from the Inorder Successor)
                pre.right = None

                count += 1

                # If count is equal to K then we
                # found the kth smallest and so
                # store it in ksmall
                if count == k:
                    ksmall = curr.key

                curr = curr.right
    return ksmall # return the found value

# A utility function to insert a new
# node with given key in BST
def insert(node, key):

    # If the tree is empty,
    # return a new node
    if node == None:
        return Node(key)

    # Otherwise, recur down the tree
    if key < node.key:
        node.left = insert(node.left, key)
    elif key > node.key:
        node.right = insert(node.right, key)

    # return the (unchanged) node pointer
    return node

# Driver Code
if __name__ == '__main__':

    # Let us create following BST
    #         50
    #       /    \
    #      30    70
    #    /  \  /  \
    #   20 40 60 80
    root = None
    root = insert(root, 50)
    insert(root, 30)
    insert(root, 20)
    insert(root, 40)
    insert(root, 70)
    insert(root, 60)
    insert(root, 80)

    for k in range(1,8):
        print(KSmallestUsingMorris(root, k),
                                 end = " ")

# This code is contributed by PranchalK

C#

// C# program to find k'th smallest element in BST
using System;

class GfG
{

// A BST node
public class Node
{
    public int key;
    public Node left, right;
}

// A function to find
static int KSmallestUsingMorris(Node root, int k)
{
    // Count to iterate over elements till we
    // get the kth smallest number
    int count = 0;

    int ksmall = int.MinValue; // store the Kth smallest
    Node curr = root; // to store the current node

    while (curr != null)
    {
        // Like Morris traversal if current does
        // not have left child rather than printing
        // as we did in inorder, we will just
        // increment the count as the number will
        // be in an increasing order
        if (curr.left == null)
        {
            count++;

            // if count is equal to K then we found the
            // kth smallest, so store it in ksmall
            if (count==k)
                ksmall = curr.key;

            // go to current's right child
            curr = curr.right;
        }
        else
        {
            // we create links to Inorder Successor and
            // count using these links
            Node pre = curr.left;
            while (pre.right != null && pre.right != curr)
                pre = pre.right;

            // building links
            if (pre.right == null)
            {
                // link made to Inorder Successor
                pre.right = curr;
                curr = curr.left;
            }

            // While breaking the links in so made temporary
            // threaded tree we will check for the K smallest
            // condition
            else
            {
                // Revert the changes made in if part (break link
                // from the Inorder Successor)
                pre.right = null;

                count++;

                // If count is equal to K then we found
                // the kth smallest and so store it in ksmall
                if (count == k)
                    ksmall = curr.key;

                curr = curr.right;
            }
        }
    }
    return ksmall; //return the found value
}

// A utility function to create a new BST node
static Node newNode(int item)
{
    Node temp = new Node();
    temp.key = item;
    temp.left = null;
    temp.right = null;
    return temp;
}

/* A utility function to insert a new node with given key in BST */
static Node insert(Node node, int key)
{
    /* If the tree is empty, return a new node */
    if (node == null) return newNode(key);

    /* Otherwise, recur down the tree */
    if (key < node.key)
        node.left = insert(node.left, key);
    else if (key > node.key)
        node.right = insert(node.right, key);

    /* return the (unchanged) node pointer */
    return node;
}

// Driver Program to test above functions
public static void Main(String[] args)
{
    /* Let us create following BST
            50
        /     \
        30     70
        / \ / \
    20 40 60 80 */
    Node root = null;
    root = insert(root, 50);
    insert(root, 30);
    insert(root, 20);
    insert(root, 40);
    insert(root, 70);
    insert(root, 60);
    insert(root, 80);

    for (int k = 1; k <= 7; k++)
    Console.Write(KSmallestUsingMorris(root, k) + " ");

}
}

// This code has been contributed by 29AjayKumar

Javascript

<script>
// javascript program to find k'th smallest element in BST

// A BST node
     class Node {
            constructor() {
                this.key = 0;
                this.left = null;
                this.right = null;
            }
        }

// A function to find
function KSmallestUsingMorris(root , k)
{
    // Count to iterate over elements till we
    // get the kth smallest number
    var count = 0;

    var ksmall = Number.MIN_VALUE; // store the Kth smallest
    var curr = root; // to store the current node

    while (curr != null)
    {
        // Like Morris traversal if current does
        // not have left child rather than printing
        // as we did in inorder, we will just
        // increment the count as the number will
        // be in an increasing order
        if (curr.left == null)
        {
            count++;

            // if count is equal to K then we found the
            // kth smallest, so store it in ksmall
            if (count==k)
                ksmall = curr.key;

            // go to current's right child
            curr = curr.right;
        }
        else
        {
            // we create links to Inorder Successor and
            // count using these links
            var pre = curr.left;
            while (pre.right != null && pre.right != curr)
                pre = pre.right;

            // building links
            if (pre.right== null)
            {
                //link made to Inorder Successor
                pre.right = curr;
                curr = curr.left;
            }

            // While breaking the links in so made temporary
            // threaded tree we will check for the K smallest
            // condition
            else
            {
                // Revert the changes made in if part (break link
                // from the Inorder Successor)
                pre.right = null;

                count++;

                // If count is equal to K then we found
                // the kth smallest and so store it in ksmall
                if (count==k)
                    ksmall = curr.key;

                curr = curr.right;
            }
        }
    }
    return ksmall; //return the found value
}

// A utility function to create a new BST node
function newNode(item)
{
    var temp = new Node();
    temp.key = item;
    temp.left = null;
    temp.right = null;
    return temp;
}

/* A utility function to insert a new node with given key in BST */
function insert(node , key)
{
    /* If the tree is empty, return a new node */
    if (node == null) return newNode(key);

    /* Otherwise, recur down the tree */
    if (key < node.key)
        node.left = insert(node.left, key);
    else if (key > node.key)
        node.right = insert(node.right, key);

    /* return the (unchanged) node pointer */
    return node;
}

// Driver Program to test above functions

    /* Let us create following BST
            50
        /     \
        30     70
        / \ / \
    20 40 60 80 */
    var root = null;
    root = insert(root, 50);
    insert(root, 30);
    insert(root, 20);
    insert(root, 40);
    insert(root, 70);
    insert(root, 60);
    insert(root, 80);

    for (k=1; k<=7; k++)
    document.write(KSmallestUsingMorris(root, k) + " ");


// This code contributed by Rajput-Ji
</script>

Output

20 30 40 50 60 70 80 

Time Complexity: O(n) where n is the size of BST
Auxiliary Space: O(1)

Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above