Job Assignment Problem using Branch And Bound

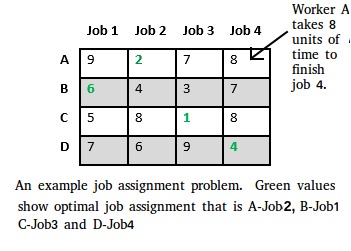
Let there be N workers and N jobs. Any worker can be assigned to perform any job, incurring some cost that may vary depending on the work-job assignment. It is required to perform all jobs by assigning exactly one worker to each job and exactly one job to each agent in such a way that the total cost of the assignment is minimized.

Let us explore all approaches for this problem.

Solution 1: Brute Force

We generate n! possible job assignments and for each such assignment, we compute its total cost and return the less expensive assignment. Since the solution is a permutation of the n jobs, its complexity is O(n!).

Solution 2: Hungarian Algorithm

The optimal assignment can be found using the Hungarian algorithm. The Hungarian algorithm has worst case run-time complexity of O(n^3).

Solution 3: DFS/BFS on state space tree

A state space tree is a N-ary tree with property that any path from root to leaf node holds one of many solutions to given problem. We can perform depth-first search on state space tree and but successive moves can take us away from the goal rather than bringing closer. The search of state space tree follows leftmost path from the root regardless of initial state. An answer node may never be found in this approach. We can also perform a Breadth-first search on state space tree. But no matter what the initial state is, the algorithm attempts the same sequence of moves like DFS.

Solution 4: Finding Optimal Solution using Branch and Bound

The selection rule for the next node in BFS and DFS is “blind”. i.e. the selection rule does not give any preference to a node that has a very good chance of getting the search to an answer node quickly. The search for an optimal solution can often be speeded by using an “intelligent” ranking function, also called an approximate cost function to avoid searching in sub-trees that do not contain an optimal solution. It is similar to BFS-like search but with one major optimization. Instead of following FIFO order, we choose a live node with least cost. We may not get optimal solution by following node with least promising cost, but it will provide very good chance of getting the search to an answer node quickly.

There are two approaches to calculate the cost function:  

1. For each worker, we choose job with minimum cost from list of unassigned jobs (take minimum entry from each row).
2. For each job, we choose a worker with lowest cost for that job from list of unassigned workers (take minimum entry from each column).

In this article, the first approach is followed.

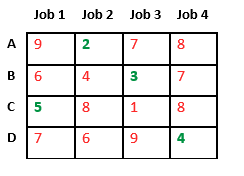
Let’s take below example and try to calculate promising cost when Job 2 is assigned to worker A. 

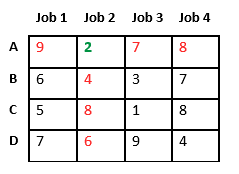
Since Job 2 is assigned to worker A (marked in green), cost becomes 2 and Job 2 and worker A becomes unavailable (marked in red). 

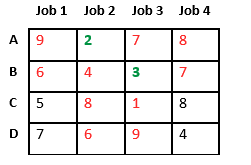
Now we assign job 3 to worker B as it has minimum cost from list of unassigned jobs. Cost becomes 2 + 3 = 5 and Job 3 and worker B also becomes unavailable. 

Finally, job 1 gets assigned to worker C as it has minimum cost among unassigned jobs and job 4 gets assigned to worker D as it is only Job left. Total cost becomes 2 + 3 + 5 + 4 = 14. 

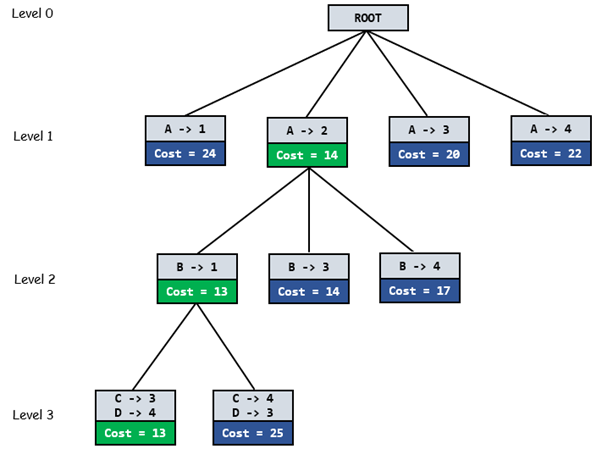
Below diagram shows complete search space diagram showing optimal solution path in green. 

Complete Algorithm:

/* findMinCost uses Least() and Add() to maintain the
   list of live nodes

   Least() finds a live node with least cost, deletes
   it from the list and returns it

   Add(x) calculates cost of x and adds it to the list
   of live nodes

   Implements list of live nodes as a min heap */

// Search Space Tree Node
node
{
   int job_number;
   int worker_number;
   node parent;
   int cost;
}

// Input: Cost Matrix of Job Assignment problem
// Output: Optimal cost and Assignment of Jobs
algorithm findMinCost (costMatrix mat[][])
{
   // Initialize list of live nodes(min-Heap)
   // with root of search tree i.e. a Dummy node
   while (true)
   {
      // Find a live node with least estimated cost
      E = Least();

      // The found node is deleted from the list
      // of live nodes
      if (E is a leaf node)
      {
         printSolution();
         return;
      }

     for each child x of E
     {
         Add(x); // Add x to list of live nodes;
         x->parent = E; // Pointer for path to root
     }
   }
} 

Below is the implementation of the above approach:

C++

// Program to solve Job Assignment problem
// using Branch and Bound
#include <bits/stdc++.h>
using namespace std;
#define N 4

// state space tree node
struct Node
{
    // stores parent node of current node
    // helps in tracing path when answer is found
    Node* parent;

    // contains cost for ancestors nodes
    // including current node
    int pathCost;

    // contains least promising cost
    int cost;

    // contain worker number
    int workerID;

    // contains Job ID
    int jobID;

    // Boolean array assigned will contains
    // info about available jobs
    bool assigned[N];
};

// Function to allocate a new search tree node
// Here Person x is assigned to job y
Node* newNode(int x, int y, bool assigned[],
              Node* parent)
{
    Node* node = new Node;

    for (int j = 0; j < N; j++)
        node->assigned[j] = assigned[j];
    node->assigned[y] = true;

    node->parent = parent;
    node->workerID = x;
    node->jobID = y;

    return node;
}

// Function to calculate the least promising cost
// of node after worker x is assigned to job y.
int calculateCost(int costMatrix[N][N], int x,
                  int y, bool assigned[])
{
    int cost = 0;

    // to store unavailable jobs
    bool available[N] = {true};

    // start from next worker
    for (int i = x + 1; i < N; i++)
    {
        int min = INT_MAX, minIndex = -1;

        // do for each job
        for (int j = 0; j < N; j++)
        {
            // if job is unassigned
            if (!assigned[j] && available[j] &&
                costMatrix[i][j] < min)
            {
                // store job number
                minIndex = j;

                // store cost
                min = costMatrix[i][j];
            }
        }

        // add cost of next worker
        cost += min;

        // job becomes unavailable
        available[minIndex] = false;
    }

    return cost;
}

// Comparison object to be used to order the heap
struct comp
{
    bool operator()(const Node* lhs,
                   const Node* rhs) const
    {
        return lhs->cost > rhs->cost;
    }
};

// print Assignments
void printAssignments(Node *min)
{
    if(min->parent==NULL)
        return;

    printAssignments(min->parent);
    cout << "Assign Worker " << char(min->workerID + 'A')
         << " to Job " << min->jobID << endl;

}

// Finds minimum cost using Branch and Bound.
int findMinCost(int costMatrix[N][N])
{
    // Create a priority queue to store live nodes of
    // search tree;
    priority_queue<Node*, std::vector<Node*>, comp> pq;

    // initialize heap to dummy node with cost 0
    bool assigned[N] = {false};
    Node* root = newNode(-1, -1, assigned, NULL);
    root->pathCost = root->cost = 0;
    root->workerID = -1;

    // Add dummy node to list of live nodes;
    pq.push(root);

    // Finds a live node with least cost,
    // add its childrens to list of live nodes and
    // finally deletes it from the list.
    while (!pq.empty())
    {
      // Find a live node with least estimated cost
      Node* min = pq.top();

      // The found node is deleted from the list of
      // live nodes
      pq.pop();

      // i stores next worker
      int i = min->workerID + 1;

      // if all workers are assigned a job
      if (i == N)
      {
          printAssignments(min);
          return min->cost;
      }

      // do for each job
      for (int j = 0; j < N; j++)
      {
        // If unassigned
        if (!min->assigned[j])
        {
          // create a new tree node
          Node* child = newNode(i, j, min->assigned, min);

          // cost for ancestors nodes including current node
          child->pathCost = min->pathCost + costMatrix[i][j];

          // calculate its lower bound
          child->cost = child->pathCost +
            calculateCost(costMatrix, i, j, child->assigned);

          // Add child to list of live nodes;
          pq.push(child);
        }
      }
    }
}

// Driver code
int main()
{
    // x-coordinate represents a Worker
    // y-coordinate represents a Job
    int costMatrix[N][N] =
    {
        {9, 2, 7, 8},
        {6, 4, 3, 7},
        {5, 8, 1, 8},
        {7, 6, 9, 4}
    };


    /* int costMatrix[N][N] =
    {
        {82, 83, 69, 92},
        {77, 37, 49, 92},
        {11, 69,  5, 86},
        { 8,  9, 98, 23}
    };
    */

    /* int costMatrix[N][N] =
    {
        {2500, 4000, 3500},
        {4000, 6000, 3500},
        {2000, 4000, 2500}
    };*/

    /*int costMatrix[N][N] =
    {
        {90, 75, 75, 80},
        {30, 85, 55, 65},
        {125, 95, 90, 105},
        {45, 110, 95, 115}
    };*/


    cout << "\nOptimal Cost is "
        << findMinCost(costMatrix);

    return 0;
}

Java

import java.util.*;

// Node class represents a job assignment
class Node {
    Node parent; // parent node
    int pathCost; // cost to reach this node
    int cost; // lower bound cost
    int workerID; // worker ID
    int jobID; // job ID
    boolean assigned[]; // keeps track of assigned jobs

    public Node(int N) {
        assigned = new boolean[N]; // initialize assigned jobs array
    }
}

public class Main {
    static final int N = 4; // number of workers and jobs

    // Function to create a new search tree node
    static Node newNode(int x, int y, boolean assigned[], Node parent) {
        Node node = new Node(N);
        for (int j = 0; j < N; j++)
            node.assigned[j] = assigned[j];
        if (y != -1) {
            node.assigned[y] = true;
        }
        node.parent = parent;
        node.workerID = x;
        node.jobID = y;
        return node;
    }

    // Function to calculate the least promising cost of a node
    static int calculateCost(int costMatrix[][], int x, int y, boolean assigned[]) {
        int cost = 0;
        boolean available[] = new boolean[N];
        Arrays.fill(available, true);

        for (int i = x + 1; i < N; i++) {
            int min = Integer.MAX_VALUE, minIndex = -1;
            for (int j = 0; j < N; j++) {
                if (!assigned[j] && available[j] && costMatrix[i][j] < min) {
                    minIndex = j;
                    min = costMatrix[i][j];
                }
            }
            cost += min;
            available[minIndex] = false;
        }
        return cost;
    }

    // Function to print job assignment
    static void printAssignments(Node min) {
        if (min.parent == null)
            return;
        printAssignments(min.parent);
        System.out.println("Assign Worker " + (char)(min.workerID + 'A') + " to Job " + min.jobID);
    }

    // Function to solve Job Assignment Problem using Branch and Bound
    static int findMinCost(int costMatrix[][]) {
        PriorityQueue<Node> pq = new PriorityQueue<>(Comparator.comparingInt(node -> node.cost));
        boolean assigned[] = new boolean[N];
        Node root = newNode(-1, -1, assigned, null);
        root.pathCost = root.cost = 0;
        root.workerID = -1;
        pq.add(root);

        while (!pq.isEmpty()) {
            Node min = pq.poll();
            int i = min.workerID + 1;
            if (i == N) {
                printAssignments(min);
                return min.cost;
            }
            for (int j = 0; j < N; j++) {
                if (!min.assigned[j]) {
                    Node child = newNode(i, j, min.assigned, min);
                    child.pathCost = min.pathCost + costMatrix[i][j];
                    child.cost = child.pathCost + calculateCost(costMatrix, i, j, child.assigned);
                    pq.add(child);
                }
            }
        }
        return 0;
    }

    public static void main(String[] args) {
        int costMatrix[][] = {
            {9, 2, 7, 8},
            {6, 4, 3, 7},
            {5, 8, 1, 8},
            {7, 6, 9, 4}
        };
        System.out.println("\nOptimal Cost is " + findMinCost(costMatrix));
    }
}

Python

import heapq
import copy

N = 4

# State space tree node
class Node:
    def __init__(self, x, y, assigned, parent):
        self.parent = parent
        self.pathCost = 0
        self.cost = 0
        self.workerID = x
        self.jobID = y
        self.assigned = copy.deepcopy(assigned)
        if y != -1:
            self.assigned[y] = True

# Custom heap class with push and pop functions
class CustomHeap:
    def __init__(self):
        self.heap = []

    def push(self, node):
        heapq.heappush(self.heap, (node.cost, node))

    def pop(self):
        if self.heap:
            _, node = heapq.heappop(self.heap)
            return node
        return None

# Function to allocate a new search tree node
# Here Person x is assigned to job y
def new_node(x, y, assigned, parent):
    return Node(x, y, assigned, parent)

# Function to calculate the least promising cost
# of node after worker x is assigned to job y.
def calculate_cost(cost_matrix, x, y, assigned):
    cost = 0

    # to store unavailable jobs
    available = [True] * N

    # start from the next worker
    for i in range(x + 1, N):
        min_val, min_index = float('inf'), -1

        # do for each job
        for j in range(N):
            # if job is unassigned
            if not assigned[j] and available[j] and cost_matrix[i][j] < min_val:
                # store job number
                min_index = j

                # store cost
                min_val = cost_matrix[i][j]

        # add cost of next worker
        cost += min_val

        # job becomes unavailable
        available[min_index] = False

    return cost

# Comparison object to be used to order the heap
class Comp:
    def __init__(self, node):
        self.node = node

    def __lt__(self, other):
        return self.node.cost > other.node.cost

# Print Assignments
def print_assignments(min_node):
    if min_node.parent is None:
        return

    print_assignments(min_node.parent)
    print("Assign Worker {} to Job {}".format(chr(min_node.workerID + ord('A')), min_node.jobID))

# Finds minimum cost using Branch and Bound
def find_min_cost(cost_matrix):
    # Create a priority queue to store live nodes of the search tree
    pq = CustomHeap()

    # initialize heap to dummy node with cost 0
    assigned = [False] * N
    root = new_node(-1, -1, assigned, None)
    root.pathCost = root.cost = 0
    root.workerID = -1

    # Add dummy node to list of live nodes;
    pq.push(root)

    # Finds a live node with least estimated cost,
    # add its children to the list of live nodes and
    # finally deletes it from the list.
    while True:
        # Find a live node with least estimated cost
        min_node = pq.pop()

        # i stores the next worker
        i = min_node.workerID + 1

        # if all workers are assigned a job
        if i == N:
            print_assignments(min_node)
            return min_node.cost

        # do for each job
        for j in range(N):
            # If unassigned
            if not min_node.assigned[j]:
                # create a new tree node
                child = new_node(i, j, min_node.assigned, min_node)

                # cost for ancestors nodes including the current node
                child.pathCost = min_node.pathCost + cost_matrix[i][j]

                # calculate its lower bound
                child.cost = child.pathCost + calculate_cost(cost_matrix, i, j, child.assigned)

                # Add child to list of live nodes;
                pq.push(child)

# Driver code
if __name__ == "__main__":
    # x-coordinate represents a Worker
    # y-coordinate represents a Job
    cost_matrix = [
        [9, 2, 7, 8],
        [6, 4, 3, 7],
        [5, 8, 1, 8],
        [7, 6, 9, 4]
    ]

    # Optimal Cost
    optimal_cost = find_min_cost(cost_matrix)
    if optimal_cost is not None:
        print("\nOptimal Cost is {}".format(optimal_cost))
    else:
        print("\nNo optimal solution found.")

C#

using System;
using System.Collections.Generic;

public class Node
{
    public Node parent;         // Parent node in the state space tree
    public int pathCost;        // Path cost from root to this node
    public int cost;            // Total cost for this node
    public int workerID;        // ID of the worker
    public int jobID;           // ID of the job
    public bool[] assigned;     // Array indicating which jobs are assigned

    // Constructor to initialize a node
    public Node(int x, int y, bool[] assigned, Node parent)
    {
        this.parent = parent;
        this.pathCost = 0;
        this.cost = 0;
        this.workerID = x;
        this.jobID = y;
        // Deep copy of the assigned array to prevent modification of the original
        this.assigned = (bool[])assigned.Clone();
        if (y != -1)
            this.assigned[y] = true;   // Marking the job as assigned if it's not -1
    }
}

// Custom implementation of a min heap
public class CustomHeap
{
    private List<(int, Node)> heap;   // List to store nodes and their costs

    // Constructor to initialize the heap
    public CustomHeap()
    {
        heap = new List<(int, Node)>();
    }

    // Method to push a node into the heap
    public void Push(Node node)
    {
        heap.Add((node.cost, node));   // Adding node with its cost to the heap
        heap.Sort((x, y) => x.Item1.CompareTo(y.Item1));   // Sorting the heap based on costs
    }

    // Method to pop the node with the minimum cost from the heap
    public Node Pop()
    {
        if (heap.Count > 0)
        {
            var node = heap[0].Item2;   // Extracting the node with minimum cost
            heap.RemoveAt(0);           // Removing the node from the heap
            return node;                // Returning the extracted node
        }
        return null;
    }
}

public class BranchAndBound
{
    private static int N = 4;   // Number of workers and jobs

    // Method to create a new node
    public static Node NewNode(int x, int y, bool[] assigned, Node parent)
    {
        return new Node(x, y, assigned, parent);   // Creating a new node and returning it
    }

    // Method to calculate the cost of assigning a worker to a job
    public static int CalculateCost(int[][] costMatrix, int x, int y, bool[] assigned)
    {
        int cost = 0;
        bool[] available = new bool[N];
        for (int i = 0; i < N; i++)
        {
            available[i] = true;   // Initializing all jobs as available
        }

        // Loop through the remaining workers
        for (int i = x + 1; i < N; i++)
        {
            int minVal = int.MaxValue;
            int minIndex = -1;

            // Find the minimum cost job for the current worker
            for (int j = 0; j < N; j++)
            {
                if (!assigned[j] && available[j] && costMatrix[i][j] < minVal)
                {
                    minIndex = j;
                    minVal = costMatrix[i][j];
                }
            }
            cost += minVal;          // Add the cost of the assigned job to the total cost
            available[minIndex] = false;    // Mark the assigned job as unavailable
        }
        return cost;    // Return the total cost
    }

    // Method to print the assignments recursively
    public static void PrintAssignments(Node minNode)
    {
        if (minNode.parent == null)
            return;

        PrintAssignments(minNode.parent);
        Console.WriteLine($"Assign Worker {(char)(minNode.workerID + 'A')} to Job {minNode.jobID}");
    }

    // Method to find the minimum cost using Branch and Bound algorithm
    public static int FindMinCost(int[][] costMatrix)
    {
        CustomHeap pq = new CustomHeap();   // Priority queue to store live nodes
        bool[] assigned = new bool[N];
        Node root = NewNode(-1, -1, assigned, null);    // Root node with dummy values
        root.pathCost = root.cost = 0;
        root.workerID = -1;
        pq.Push(root);    // Pushing the root node into the priority queue

        while (true)
        {
            Node minNode = pq.Pop();    // Pop the node with the minimum cost

            int i = minNode.workerID + 1;

            if (i == N)
            {
                PrintAssignments(minNode);    // Print the assignments if all workers are assigned jobs
                return minNode.cost;          // Return the minimum cost
            }

            for (int j = 0; j < N; j++)
            {
                if (!minNode.assigned[j])
                {
                    Node child = NewNode(i, j, minNode.assigned, minNode);    // Create a new node
                    child.pathCost = minNode.pathCost + costMatrix[i][j];     // Calculate path cost
                    child.cost = child.pathCost + CalculateCost(costMatrix, i, j, child.assigned);   // Calculate total cost
                    pq.Push(child);   // Push the child node into the priority queue
                }
            }
        }
    }

    // Main method
    static void Main(string[] args)
    {
        int[][] costMatrix = new int[][] {
            new int[] { 9, 2, 7, 8 },
            new int[] { 6, 4, 3, 7 },
            new int[] { 5, 8, 1, 8 },
            new int[] { 7, 6, 9, 4 }
        };

        int optimalCost = FindMinCost(costMatrix);   // Find the optimal cost using Branch and Bound
        if (optimalCost != int.MaxValue)
            Console.WriteLine($"\nOptimal Cost is {optimalCost}");   // Print the optimal cost
        else
            Console.WriteLine("\nNo optimal solution found.");   // Print a message if no optimal solution is found
    }
}

JavaScript

// Define the size of the problem
const N = 4;

// Function to calculate the least promising cost
// of node after worker x is assigned to job y.
function calculateCost(costMatrix, x, y, assigned) {
    let cost = 0;

    // to store unavailable jobs
    let available = Array(N).fill(true);

    // start from next worker
    for (let i = x + 1; i < N; i++) {
        let min = Number.MAX_SAFE_INTEGER, minIndex = -1;

        // do for each job
        for (let j = 0; j < N; j++) {
            // if job is unassigned
            if (!assigned[j] && available[j] && costMatrix[i][j] < min) {
                // store job number
                minIndex = j;

                // store cost
                min = costMatrix[i][j];
            }
        }

        // add cost of next worker
        cost += min;

        // job becomes unavailable
        available[minIndex] = false;
    }

    return cost;
}

// print Assignments
function printAssignments(min) {
    if(min.parent == null)
        return;

    printAssignments(min.parent);
    console.log("Assign Worker " + String.fromCharCode('A'.charCodeAt(0) + min.workerID) + " to Job " + min.jobID);
}

// Finds minimum cost using Branch and Bound.
function findMinCost(costMatrix) {
    // Create a priority queue to store live nodes of
    // search tree;
    let pq = [];

    // initialize heap to dummy node with cost 0
    let assigned = Array(N).fill(false);
    let root = {parent: null, workerID: -1, pathCost: 0, cost: 0, assigned: assigned};

    // Add dummy node to list of live nodes;
    pq.push(root);

    // Finds a live node with least cost,
    // add its childrens to list of live nodes and
    // finally deletes it from the list.
    while (pq.length > 0) {
        // Find a live node with least estimated cost
        let min = pq.shift();

        // i stores next worker
        let i = min.workerID + 1;

        // if all workers are assigned a job
        if (i == N) {
            printAssignments(min);
            return min.cost;
        }

        // do for each job
        for (let j = 0; j < N; j++) {
            // If unassigned
            if (!min.assigned[j]) {
                // create a new tree node
                let child = {parent: min, workerID: i, jobID: j, pathCost: min.pathCost + costMatrix[i][j], assigned: [...min.assigned]};
                child.assigned[j] = true;

                // calculate its lower bound
                child.cost = child.pathCost + calculateCost(costMatrix, i, j, child.assigned);

                // Add child to list of live nodes;
                pq.push(child);
            }
        }

        // sort the queue in ascending order of cost
        pq.sort((a, b) => a.cost - b.cost);
    }
}

// Driver code
function main() {
    // x-coordinate represents a Worker
    // y-coordinate represents a Job
    let costMatrix = [
        [9, 2, 7, 8],
        [6, 4, 3, 7],
        [5, 8, 1, 8],
        [7, 6, 9, 4]
    ];

    console.log("\nOptimal Cost is " + findMinCost(costMatrix));
}

main();

Output : 

Assign Worker A to Job 1
Assign Worker B to Job 0
Assign Worker C to Job 2
Assign Worker D to Job 3

Optimal Cost is 13

Time Complexity: O(M*N). This is because the algorithm uses a double for loop to iterate through the M x N matrix. 
Auxiliary Space: O(M+N). This is because it uses two arrays of size M and N to track the applicants and jobs.