Javascript Program to multiply two matrices

Given two matrices, the task to multiply them. Matrices can either be square or rectangular.

Examples:

Input : mat1[][] = {{1, 2}, 
                   {3, 4}}
        mat2[][] = {{1, 1}, 
                    {1, 1}}
Output : {{3, 3}, 
          {7, 7}}
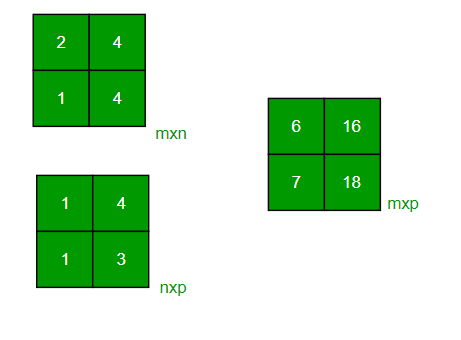
Input : mat1[][] = {{2, 4}, 
                    {3, 4}}
        mat2[][] = {{1, 2}, 
                    {1, 3}}       
Output : {{6, 16}, 
          {7, 18}}

Multiplication of Square Matrices : 
The below program multiplies two square matrices of size 4*4, we can change N for different dimensions. 

Javascript

<script>

// Javascript program to multiply
// two square matrices.

const N = 4;

// This function multiplies
// mat1[][] and mat2[][], and
// stores the result in res[][]
function multiply(mat1, mat2, res)
{
    let i, j, k;
    for (i = 0; i < N; i++) {
        for (j = 0; j < N; j++) {
            res[i][j] = 0;
            for (k = 0; k < N; k++)
                res[i][j] += mat1[i][k] * mat2[k][j];
        }
    }
}

// Driver Code
    let i, j;

    // To store result
    let res = new Array(N);
    for (let k = 0; k < N; k++)
        res[k] = new Array(N);

    let mat1 = [ [ 1, 1, 1, 1 ],
                       [ 2, 2, 2, 2 ],
                       [ 3, 3, 3, 3 ],
                       [ 4, 4, 4, 4 ] ];

    let mat2 = [ [ 1, 1, 1, 1 ],
                       [ 2, 2, 2, 2 ],
                       [ 3, 3, 3, 3 ],
                       [ 4, 4, 4, 4 ] ];

    multiply(mat1, mat2, res);

    document.write("Result matrix is <br>");
    for (i = 0; i < N; i++) {
        for (j = 0; j < N; j++)
            document.write(res[i][j] + " ");
        document.write("<br>");
    }

</script>

Output

Result matrix is 
10 10 10 10 
20 20 20 20 
30 30 30 30 
40 40 40 40

Time complexity: O(n³). It can be optimized using Strassen’s Matrix Multiplication

Auxiliary Space: O(n²)

Multiplication of Rectangular Matrices : 
We use pointers in C to multiply to matrices. Please refer to the following post as a prerequisite of the code.
How to pass a 2D array as a parameter in C?

Javascript

<script>

// Javascript program to multiply two
// rectangular matrices

// Multiplies two matrices mat1[][]
// and mat2[][] and prints result.
// (m1) x (m2) and (n1) x (n2) are
// dimensions of given matrices.
function multiply(m1, m2, mat1, n1, n2, mat2)
{
    let x, i, j;
    let res = new Array(m1);
    for (i = 0; i < m1; i++)
        res[i] = new Array(n2);

    for (i = 0; i < m1; i++)
    {
        for (j = 0; j < n2; j++)
        {
            res[i][j] = 0;
            for (x = 0; x < m2; x++)
            {
                res[i][j] += mat1[i][x] * mat2[x][j];
            }
        }
    }
    for (i = 0; i < m1; i++)
    {
        for (j = 0; j < n2; j++)
        {
            document.write(res[i][j] + " ");
        }
        document.write("<br>");
    }
}

// Driver code
    let mat1 = [ [ 2, 4 ], [ 3, 4 ] ];
    let mat2 = [ [ 1, 2 ], [ 1, 3 ] ];
    let m1 = 2, m2 = 2, n1 = 2, n2 = 2;

    // Function call
    multiply(m1, m2, mat1, n1, n2, mat2);

</script>

Output

6 16 
7 18

Time complexity: O(n³). It can be optimized using Strassen’s Matrix Multiplication

Auxiliary Space: O(m1 * n2)

Please refer complete article on Program to multiply two matrices for more details!