Java Program to print all permutations of a given string
Last Updated :
10 Dec, 2021
A permutation also called an “arrangement number” or “order,” is a rearrangement of the elements of an ordered list S into a one-to-one correspondence with S itself. A string of length n has n! permutation.
Source: Mathword(http://mathworld.wolfram.com/Permutation.html)
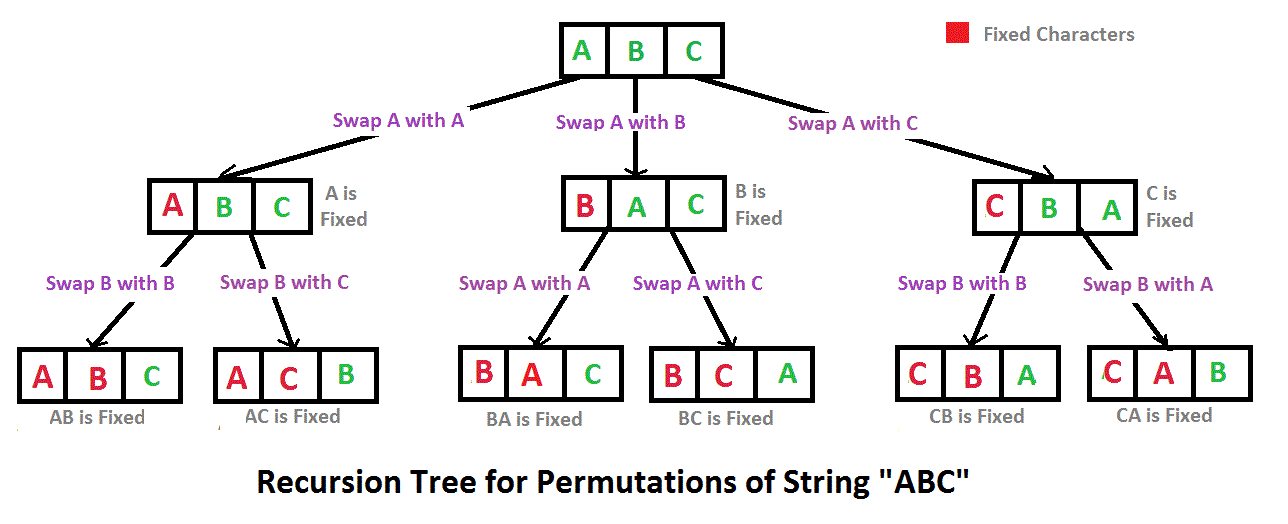
Below are the permutations of string ABC.
ABC ACB BAC BCA CBA CAB
Here is a solution that is used as a basis in backtracking.
Java
public class Permutation
{
public static void main(String[] args)
{
String str = "ABC";
int n = str.length();
Permutation permutation =
new Permutation();
permutation.permute(str, 0, n-1);
}
private void permute(String str,
int l, int r)
{
if (l == r)
System.out.println(str);
else
{
for (int i = l; i <= r; i++)
{
str = swap(str,l,i);
permute(str, l+1, r);
str = swap(str,l,i);
}
}
}
public String swap(String a,
int i, int j)
{
char temp;
char[] charArray = a.toCharArray();
temp = charArray[i] ;
charArray[i] = charArray[j];
charArray[j] = temp;
return String.valueOf(charArray);
}
}
|
Output:
ABC
ACB
BAC
BCA
CBA
CAB
Algorithm Paradigm: Backtracking
Time Complexity: O(n*n!) Note that there are n! permutations and it requires O(n) time to print a permutation.
Auxiliary Space: O(r – l)
Note: The above solution prints duplicate permutations if there are repeating characters in the input string. Please see the below link for a solution that prints only distinct permutations even if there are duplicates in input.
Print all distinct permutations of a given string with duplicates.
Permutations of a given string using STL
Another approach:
Java
import java.util.*;
class GFG{
static void permute(String s,
String answer)
{
if (s.length() == 0)
{
System.out.print(answer + " ");
return;
}
for(int i = 0 ;i < s.length(); i++)
{
char ch = s.charAt(i);
String left_substr = s.substring(0, i);
String right_substr = s.substring(i + 1);
String rest = left_substr + right_substr;
permute(rest, answer + ch);
}
}
public static void main(String args[])
{
Scanner scan = new Scanner(System.in);
String s;
String answer="";
System.out.print(
"Enter the string : ");
s = scan.next();
System.out.print(
"\nAll possible strings are : ");
permute(s, answer);
}
}
|
Output:
Enter the string : abc
All possible strings are : abc acb bac bca cab cba
Time Complexity: O(n*n!) The time complexity is the same as the above approach, i.e. there are n! permutations and it requires O(n) time to print a permutation.
Auxiliary Space: O(|s|)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...