Java Program to Find Chromatic Index of Cyclic Graphs

Chromatic Index of a graph is the minimum number of colours required to colour the edges of the graph such that any two edges that share the same vertex have different colours.

Whereas, the cyclic graph is a graph that contains at least one graph cycle i.e. cyclic means a path from at least one node back to itself. Here given, the cyclic graph we have to find the chromatic index of that graph.

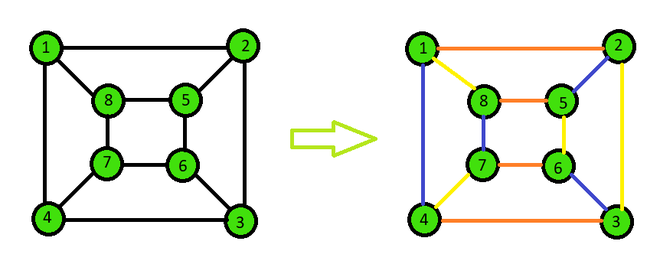
Examples:

Input: e = 12

           edges = {{ 1, 2}, { 2, 3}, { 3, 4},

                          { 4, 1}, { 5, 6}, { 6, 7},

                          { 7, 8}, { 8, 5}, { 1, 8},

                          { 2, 5}, { 3, 6}, { 4, 7}}

Output: Chromatic Index = 3

Explanation:

Approach:

By applying Vizing’s Theorem we can prove that a given graph can have a chromatic index of ‘d’ or ‘d’+1, where d is the maximum degree of the graph.

Below is the step-by-step approach of the algorithm:-

1. Initialize the number of edges and the edge list.
2. Color the graph according to the Vizing’s Theorem.
3. Assign a color to an edge and check if any adjacent edges have the same color or not.
4. If any adjacent edge has the same color, then increment the color to try the next color for that edge.
5. Repeat till all the edges get it’s color according to the theorem.
6. Once done print the maximum value of color for all the edges and the colors of every edge.

Below is the implementation of the above approach:

Java

// Java program to find the chromatic
// index of a cyclic graph
import java.util.*;

public class chromaticIndex {

    // Function to find the chromatic index
    public void edgeColoring(int[][] edges, int e)
    {
        // Initialize edge to first
        // edge and color to color 1
        int i = 0, color = 1;

        // Repeat until all edges are done coloring
        while (i < e) {
            // Give the selected edge a color
            edges[i][2] = color;
            boolean flag = false;
            // Iterate through all others edges to check
            for (int j = 0; j < e; j++) {
                // Ignore if same edge
                if (j == i)
                    continue;
                // Check if one vertex is similar
                if ((edges[i][0] == edges[j][0])
                    || (edges[i][1] == edges[j][0])
                    || (edges[i][0] == edges[j][1])
                    || (edges[i][1] == edges[j][1])) {
                    // Check if color is similar
                    if (edges[i][2] == edges[j][2]) {
                        // Increment the color by 1
                        color++;
                        flag = true;
                        break;
                    }
                }
            }

            // If same color faced then repeat again
            if (flag == true) {
                continue;
            }

            // Or else proceed to a new vertex with color 1
            color = 1;
            i++;
        }

        // Check the maximum color from all the edge colors
        int maxColor = -1;
        for (i = 0; i < e; i++) {
            maxColor = Math.max(maxColor, edges[i][2]);
        }

        // Print the chromatic index
        System.out.println("Chromatic Index = " + maxColor);
    }

    // Driver code
    public static void main(String[] args)
    {

        // Number of edges
        int e = 4;

        // Edge list
        int[][] edges = new int[e][3];

        // Initialize all edge colors to 0
        for (int i = 0; i < e; i++) {
            edges[i][2] = -1;
        }

        // Edges
        edges[0][0] = 1;
        edges[0][1] = 2;

        edges[1][0] = 2;
        edges[1][1] = 3;

        edges[2][0] = 3;
        edges[2][1] = 4;

        edges[3][0] = 4;
        edges[3][1] = 1;

        // Run the function
        chromaticIndex c = new chromaticIndex();
        c.edgeColoring(edges, e);
    }
}

Output

Chromatic Index = 2

Time Complexity: O(e²)

Auxiliary Space: O(1)

As constant extra space is used.

References: 

1. vizings-theorem
2. https://en.wikipedia.org/wiki/Vizing%27s_theorem