Java Program for Legendre’s Conjecture

It says that there is always one prime number between any two consecutive natural number\’s(n = 1, 2, 3, 4, 5, …) square. This is called Legendre’s Conjecture. Conjecture: A conjecture is a proposition or conclusion based upon incomplete information to which no proof has been found i.e it has not been proved or disproved.

Mathematically, there is always one prime p in the range 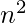to 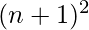where n is any natural number. for examples- 2 and 3 are the primes in the range 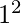to . 5 and 7 are the primes in the range to 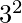. 11 and 13 are the primes in the range 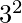to 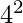. 17 and 19 are the primes in the range 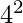to .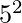

Examples:

Input : 4 
output: Primes in the range 16 and 25 are:
        17
        19
        23

Explanation: Here 4² = 16 and 5² = 25 Hence, prime numbers between 16 and 25 are 17, 19 and 23.

Input : 10
Output: Primes in the range 100 and 121 are:
        101
        103
        107
        109
        113

Java

// Java program to verify Legendre's Conjecture
// for a given n.
class GFG {

  // prime checking
  static boolean isprime(int n)
  {
     for (int i = 2; i * i <= n; i++)
        if (n % i == 0)
            return false;
     return true;
  }

  static void LegendreConjecture(int n)
  {
     System.out.println("Primes in the range "+n*n
        +" and "+(n+1)*(n+1)
        +" are:");

     for (int i = n*n; i <= ((n+1)*(n+1)); i++)
     {
       // searching for primes
       if (isprime(i))
         System.out.println(i);
     }
  }

  // Driver program
  public static void main(String[] args)
  {
     int n = 50;
     LegendreConjecture(n);
  }
}
//This code is contributed by
//Smitha Dinesh Semwal

Please refer complete article on Legendre’s Conjecture for more details!