Java Program for Breadth First Search or BFS for a Graph
Last Updated :
21 Mar, 2024
The Breadth First Search (BFS) algorithm is used to search a graph data structure for a node that meets a set of criteria. It starts at the root of the graph and visits all nodes at the current depth level before moving on to the nodes at the next depth level.
Relation between BFS for Graph and Tree Traversal
Breadth-First Traversal (or Search) for a graph is similar to the Breadth-First Traversal of a tree. The only catch here is, that, unlike trees, graphs may contain cycles, so we may come to the same node again. To avoid processing a node more than once, we divide the vertices into two categories:
A Boolean visited array is used to mark the visited vertices. For simplicity, it is assumed that all vertices are reachable from the starting vertex. BFS uses a queue data structure for traversal.
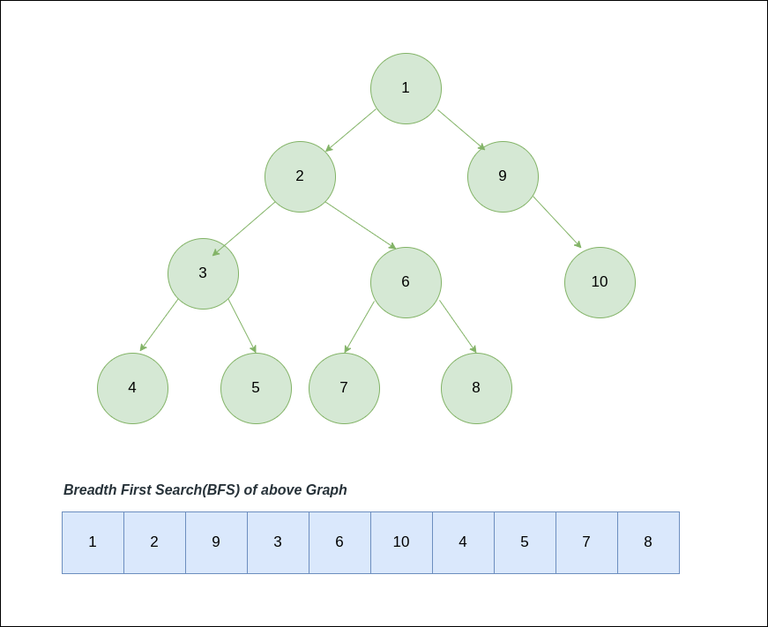
Working of Breadth-First Search
Starting from the root, all the nodes at a particular level are visited first and then the nodes of the next level are traversed till all the nodes are visited.
To do this a queue is used. All the adjacent unvisited nodes of the current level are pushed into the queue and the nodes of the current level are marked visited and popped from the queue.
Program of BFS for a Graph in Java
Below is the implementation of the above approach:
Java
// Java program to print BFS traversal from a given source
// vertex. BFS(int s) traverses vertices reachable from s.
import java.io.*;
import java.util.*;
// This class represents a directed graph using adjacency
// list representation
class Graph {
// No. of vertices
private int V;
// Adjacency Lists
private LinkedList<Integer> adj[];
// Constructor
Graph(int v)
{
V = v;
adj = new LinkedList[v];
for (int i = 0; i < v; ++i)
adj[i] = new LinkedList();
}
// Function to add an edge into the graph
void addEdge(int v, int w) { adj[v].add(w); }
// prints BFS traversal from a given source s
void BFS(int s)
{
// Mark all the vertices as not visited(By default
// set as false)
boolean visited[] = new boolean[V];
// Create a queue for BFS
LinkedList<Integer> queue
= new LinkedList<Integer>();
// Mark the current node as visited and enqueue it
visited[s] = true;
queue.add(s);
while (queue.size() != 0) {
// Dequeue a vertex from queue and print it
s = queue.poll();
System.out.print(s + " ");
// Get all adjacent vertices of the dequeued
// vertex s.
// If an adjacent has not been visited,
// then mark it visited and enqueue it
Iterator<Integer> i = adj[s].listIterator();
while (i.hasNext()) {
int n = i.next();
if (!visited[n]) {
visited[n] = true;
queue.add(n);
}
}
}
}
// Driver code
public static void main(String args[])
{
Graph g = new Graph(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
System.out.println(
"Following is Breadth First Traversal "
+ "(starting from vertex 2)");
g.BFS(2);
}
}
OutputFollowing is Breadth First Traversal (starting from vertex 2)
2 0 3 1
Complexity of the above method:
Time Complexity: O(V+E), where V is the number of nodes and E is the number of edges.
Auxiliary Space: O(V)
Please refer complete article on Breadth First Search or BFS for a Graph for more details.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...