Iterative program to count leaf nodes in a Binary Tree

Given a binary tree, count leaves in the tree without using recursion. A node is a leaf node if both left and right children of it are NULL.

  Example Tree

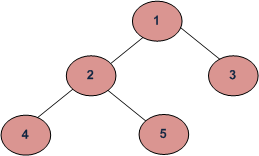
 Leaves count for the above tree is 3.

The idea is to use level order traversal. During traversal, if we find a node whose left and right children are NULL, we increment count. 

Implementation:

C++

// C++ program to count leaf nodes in a Binary Tree
#include <bits/stdc++.h>
using namespace std;

/* A binary tree Node has data, pointer to left
   child  and a pointer to right child */
struct Node
{
    int data;
    struct Node* left, *right;
};

/* Function to get the count of leaf Nodes in
   a binary tree*/
unsigned int getLeafCount(struct Node* node)
{
    // If tree is empty
    if (!node)
        return 0;

    // Initialize empty queue.
    queue<Node *> q;

    // Do level order traversal starting from root
    int count = 0; // Initialize count of leaves
    q.push(node);
    while (!q.empty())
    {
        struct Node *temp = q.front();
        q.pop();

        if (temp->left != NULL)
            q.push(temp->left);
        if (temp->right != NULL)
            q.push(temp->right);
        if (temp->left == NULL && temp->right == NULL)
            count++;
    }
    return count;
}

/* Helper function that allocates a new Node with the
   given data and NULL left and right pointers. */
struct Node* newNode(int data)
{
    struct Node* node = new Node;
    node->data = data;
    node->left = node->right = NULL;
    return (node);
}

/* Driver program to test above functions*/
int main()
{
    /*   1
        /  \
      2     3
     / \
    4   5
    Let us create Binary Tree shown in
    above example */

    struct Node *root = newNode(1);
    root->left        = newNode(2);
    root->right       = newNode(3);
    root->left->left  = newNode(4);
    root->left->right = newNode(5);

    /* get leaf count of the above created tree */
    cout << getLeafCount(root);

    return 0;
}

Java

// Java program to count leaf nodes
// in a Binary Tree
import java.util.*;

class GFG
{
    /* A binary tree Node has data,
    pointer to left child and
    a pointer to right child */
    static class Node
    {
        int data;
        Node left, right;
    }

    /* Function to get the count of
    leaf Nodes in a binary tree*/
    static int getLeafCount(Node node)
    {
        // If tree is empty
        if (node == null)
        {
            return 0;
        }

        // Initialize empty queue.
        Queue<Node> q = new LinkedList<>();

        // Do level order traversal starting from root
        int count = 0; // Initialize count of leaves
        q.add(node);
        while (!q.isEmpty())
        {
            Node temp = q.peek();
            q.poll();

            if (temp.left != null)
            {
                q.add(temp.left);
            }
            if (temp.right != null)
            {
                q.add(temp.right);
            }
            if (temp.left == null &&
                temp.right == null)
            {
                count++;
            }
        }
        return count;
    }

    /* Helper function that allocates
    a new Node with the given data
    and null left and right pointers. */
    static Node newNode(int data)
    {
        Node node = new Node();
        node.data = data;
        node.left = node.right = null;
        return (node);
    }

    // Driver Code
    public static void main(String[] args)
    {
        {
            /*   1
                / \
               2   3
              / \
             4   5
            Let us create Binary Tree shown in
            above example */
            Node root = newNode(1);
            root.left = newNode(2);
            root.right = newNode(3);
            root.left.left = newNode(4);
            root.left.right = newNode(5);

            /* get leaf count of the above created tree */
            System.out.println(getLeafCount(root));
        }
    }
}

// This code is contributed by Rajput-Ji

Python3

# Python3 program to count leaf nodes
# in a Binary Tree
from queue import Queue

# Helper function that allocates a new
# Node with the given data and None
# left and right pointers.
class newNode:
    def __init__(self, data):
        self.data = data
        self.left = self.right = None

# Function to get the count of leaf
# Nodes in a binary tree
def getLeafCount(node):

    # If tree is empty
    if (not node):
        return 0

    # Initialize empty queue.
    q = Queue()

    # Do level order traversal
    # starting from root
    count = 0 # Initialize count of leaves
    q.put(node)
    while (not q.empty()):
        temp = q.queue[0]
        q.get()

        if (temp.left != None):
            q.put(temp.left)
        if (temp.right != None):
            q.put(temp.right)
        if (temp.left == None and
            temp.right == None):
            count += 1
    return count

# Driver Code
if __name__ == '__main__':

    # 1
    # / \
    # 2 3
    # / \
    # 4 5
    # Let us create Binary Tree shown
    # in above example
    root = newNode(1)
    root.left = newNode(2)
    root.right = newNode(3)
    root.left.left = newNode(4)
    root.left.right = newNode(5)

    # get leaf count of the above
    # created tree
    print(getLeafCount(root))

# This code is contributed by PranchalK

C#

// C# program to count leaf nodes
// in a Binary Tree
using System;
using System.Collections.Generic;

class GFG
{
    /* A binary tree Node has data,
    pointer to left child and
    a pointer to right child */
    public class Node
    {
        public int data;
        public Node left, right;
    }

    /* Function to get the count of
    leaf Nodes in a binary tree*/
    static int getLeafCount(Node node)
    {
        // If tree is empty
        if (node == null)
        {
            return 0;
        }

        // Initialize empty queue.
        Queue<Node> q = new Queue<Node>();

        // Do level order traversal starting from root
        int count = 0; // Initialize count of leaves
        q.Enqueue(node);
        while (q.Count!=0)
        {
            Node temp = q.Peek();
            q.Dequeue();

            if (temp.left != null)
            {
                q.Enqueue(temp.left);
            }
            if (temp.right != null)
            {
                q.Enqueue(temp.right);
            }
            if (temp.left == null &&
                temp.right == null)
            {
                count++;
            }
        }
        return count;
    }

    /* Helper function that allocates
    a new Node with the given data
    and null left and right pointers. */
    static Node newNode(int data)
    {
        Node node = new Node();
        node.data = data;
        node.left = node.right = null;
        return (node);
    }

    // Driver Code
    public static void Main(String[] args)
    {
        {
            /* 1
                / \
            2 3
            / \
            4 5
            Let us create Binary Tree shown in
            above example */
            Node root = newNode(1);
            root.left = newNode(2);
            root.right = newNode(3);
            root.left.left = newNode(4);
            root.left.right = newNode(5);

            /* get leaf count of the above created tree */
            Console.WriteLine(getLeafCount(root));
        }
    }
}

// This code is contributed by 29AjayKumar

Javascript

<script>
// Javascript program to count leaf nodes
// in a Binary Tree

/* A binary tree Node has data,
    pointer to left child and
    a pointer to right child */
class Node
{
    /* Helper function that allocates
    a new Node with the given data
    and null left and right pointers. */
    constructor(data)
    {
        this.data=data;
        this.left=this.right=null;
    }
}

/* Function to get the count of
    leaf Nodes in a binary tree*/
function getLeafCount(node)
{
    // If tree is empty
        if (node == null)
        {
            return 0;
        }

        // Initialize empty queue.
        let q = [];

        // Do level order traversal starting from root
        let count = 0; // Initialize count of leaves
        q.push(node);
        while (q.length!=0)
        {
            let temp = q.shift();

            if (temp.left != null)
            {
                q.push(temp.left);
            }
            if (temp.right != null)
            {
                q.push(temp.right);
            }
            if (temp.left == null &&
                temp.right == null)
            {
                count++;
            }
        }
        return count;
}

 /*   1
                / \
               2   3
              / \
             4   5
            Let us create Binary Tree shown in
            above example */

let root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);

/* get leaf count of the above created tree */
document.write(getLeafCount(root));


// This code is contributed by unknown2108
</script>

Output

3

Time Complexity: O(n)

Auxiliary space: O(n)

Here is a recursive solution for the same problem:

The idea is simple we break the larger tree into smaller sub-trees and solve for them to get the final answer.

Below is the implementation of the above approach.

C++

// C++ Program for above approach
#include <iostream>
using namespace std;

// Node class
struct node
{
  int data;
  struct node* left;
  struct node* right;
};

// Program to count leaves
int countLeaves(struct node *node)
{

  // If the node itself is "null"
  // return 0, as there
  // are no leaves
  if(node == NULL)
  {
    return 0;
  }

  // It the node is a leaf then
  // both right and left
  // children will be "null"
  if(node->left == NULL && node->right == NULL)
  {
    return 1;
  }

  // Now we count the leaves in
  // the left and right
  // subtrees and return the sum
  return countLeaves(node->left) + countLeaves(node->right);
}

// Class newNode of Node type
struct node* newNode(int data)
{
  struct node* node =
    (struct node*)malloc(sizeof(struct node));
  node->data = data;
  node->left = NULL;
  node->right = NULL;
  return(node);
}

// Driver Code
int main()
{
  struct node *root  = newNode(1);
  root->left = newNode(2);
  root->right = newNode(3);
  root->left->left = newNode(4);
  root->left->right = newNode(5);

  /* get leaf count of the above
      created tree */
  cout<<countLeaves(root)<<endl;

}

// This code is contributed by rag2127

Java

// Java Program for above approach
import java.util.LinkedList;
import java.util.Queue;
import java.io.*;
import java.util.*;

class GfG
{

  // Node class
  static class Node
  {
    int data;
    Node left, right;
  }

  // Program to count leaves
  static int countLeaves(Node node)
  {

    // If the node itself is "null"
    // return 0, as there
    // are no leaves
    if (node == null)
      return 0;

    // It the node is a leaf then
    // both right and left
    // children will be "null"
    if (node.left == null &&
                node.right == null)
      return 1;

    // Now we count the leaves in
    // the left and right
    // subtrees and return the sum
    return countLeaves(node.left)
             + countLeaves(node.right);
  }

  // Class newNode of Node type
  static Node newNode(int data)
  {
    Node node = new Node();
    node.data = data;
    node.left = node.right = null;
    return (node);
  }

  // Driver Code
  public static void main(String[] args)
  {

      Node root = newNode(1);
      root.left = newNode(2);
      root.right = newNode(3);
      root.left.left = newNode(4);
      root.left.right = newNode(5);

      /* get leaf count of the above
      created tree */
      System.out.println(countLeaves(root));
  }
}
//Code by Rounik Prashar

Python3

# Python3 Program for above approach

# Node class
class Node:
    def __init__(self,x):
        self.data = x
        self.left = None
        self.right = None

# Program to count leaves
def countLeaves(node):

    # If the node itself is "None"
    # return 0, as there
    # are no leaves
    if (node == None):
        return 0

    # It the node is a leaf then
    # both right and left
    # children will be "None"
    if (node.left == None and node.right == None):
        return 1

    # Now we count the leaves in
    # the left and right
    # subtrees and return the sum
    return countLeaves(node.left) + countLeaves(node.right)

# Driver Code
if __name__ == '__main__':

    root = Node(1)
    root.left = Node(2)
    root.right = Node(3)
    root.left.left = Node(4)
    root.left.right = Node(5)

      # /* get leaf count of the above
      # created tree */
    print(countLeaves(root))

    # This code is contributed by mohit kumar 29

C#

// C# Program for above approach
using System;

// Node class
public class Node
{
    public int data;
    public Node left, right;

    public Node(int d)
    {
        data = d;
        left = right = null;
    }
}

public class BinaryTree{

public static Node root;

// Program to count leaves
static int countLeaves(Node node)
{

    // If the node itself is "null"
    // return 0, as there
    // are no leaves
    if (node == null)
    {
        return 0;
    }

    // It the node is a leaf then
    // both right and left
    // children will be "null"
    if (node.left == null &&
        node.right == null)
    {
        return 1;
    }

    // Now we count the leaves in
    // the left and right
    // subtrees and return the sum
    return countLeaves(node.left) +
           countLeaves(node.right);
}

// Driver Code
static public void Main()
{
    BinaryTree.root = new Node(1);
    BinaryTree.root.left = new Node(2);
    BinaryTree.root.right = new Node(3);
    BinaryTree.root.left.left = new Node(4);
    BinaryTree.root.left.right = new Node(5);

    // Get leaf count of the above created tree
    Console.WriteLine(countLeaves(root));
}
}

// This code is contributed by avanitrachhadiya2155

Javascript

<script>

// Javascript Program for above approach

     // Node class
    class Node
    {
    // Class newNode of Node type
        constructor(data)
        {
            this.data=data;
            this.next = this.right = null;
        }
    }

// Program to count leaves
function countLeaves(node)
{
        // If the node itself is "null"
    // return 0, as there
    // are no leaves
    if (node == null)
      return 0;

    // It the node is a leaf then
    // both right and left
    // children will be "null"
    if (node.left == null &&
                node.right == null)
      return 1;

    // Now we count the leaves in
    // the left and right
    // subtrees and return the sum
    return countLeaves(node.left)
             + countLeaves(node.right);
}

// Driver Code
let root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);

/* get leaf count of the above
      created tree */
document.write(countLeaves(root));

// This code is contributed by patel2127

</script>

Output

3

Time complexity: O(n) where n is no of nodes in given Binary Tree

Auxiliary space: O(n)

This article is contributed by Mr. Somesh Awasthi. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.