Iterative Postorder Traversal | Set 2 (Using One Stack)

We have discussed a simple iterative postorder traversal using two stacks in the previous post. In this post, an approach with only one stack is discussed.

The idea is to move down to leftmost node using left pointer. While moving down, push root and root’s right child to stack. Once we reach leftmost node, print it if it doesn’t have a right child. If it has a right child, then change root so that the right child is processed before. 

Following is detailed algorithm. 

1.1 Create an empty stack
2.1 Do following while root is not NULL
    a) Push root's right child and then root to stack.
    b) Set root as root's left child.
2.2 Pop an item from stack and set it as root.
    a) If the popped item has a right child and the right child 
       is at top of stack, then remove the right child from stack,
       push the root back and set root as root's right child.
    b) Else print root's data and set root as NULL.
2.3 Repeat steps 2.1 and 2.2 while stack is not empty.

Let us consider the following tree 

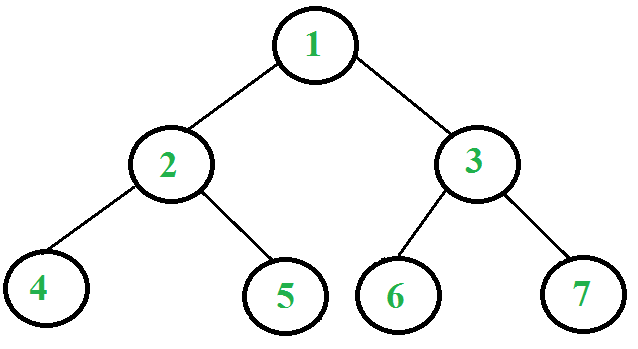
Following are the steps to print postorder traversal of the above tree using one stack.

1. Right child of 1 exists. 
   Push 3 to stack. Push 1 to stack. Move to left child.
        Stack: 3, 1

2. Right child of 2 exists. 
   Push 5 to stack. Push 2 to stack. Move to left child.
        Stack: 3, 1, 5, 2

3. Right child of 4 doesn't exist. '
   Push 4 to stack. Move to left child.
        Stack: 3, 1, 5, 2, 4

4. Current node is NULL. 
   Pop 4 from stack. Right child of 4 doesn't exist. 
   Print 4. Set current node to NULL.
        Stack: 3, 1, 5, 2

5. Current node is NULL. 
    Pop 2 from stack. Since right child of 2 equals stack top element, 
    pop 5 from stack. Now push 2 to stack.     
    Move current node to right child of 2 i.e. 5
        Stack: 3, 1, 2

6. Right child of 5 doesn't exist. Push 5 to stack. Move to left child.
        Stack: 3, 1, 2, 5

7. Current node is NULL. Pop 5 from stack. Right child of 5 doesn't exist. 
   Print 5. Set current node to NULL.
        Stack: 3, 1, 2

8. Current node is NULL. Pop 2 from stack. 
   Right child of 2 is not equal to stack top element. 
   Print 2. Set current node to NULL.
        Stack: 3, 1

9. Current node is NULL. Pop 1 from stack. 
   Since right child of 1 equals stack top element, pop 3 from stack. 
   Now push 1 to stack. Move current node to right child of 1 i.e. 3
        Stack: 1

10. Repeat the same as above steps and Print 6, 7 and 3. 
    Pop 1 and Print 1.

C++

// C++ program for iterative postorder traversal using one
// stack
#include <bits/stdc++.h>
using namespace std;

// A tree node
struct Node {
    int data;
    struct Node *left, *right;
};

// A utility function to create a new tree node
struct Node* newNode(int data)
{
    struct Node* node = new Node;
    node->data = data;
    node->left = node->right = NULL;
    return node;
}

// An iterative function to do postorder traversal of a
// given binary tree
vector<int> postOrderIterative(struct Node* root)
{
    vector<int> postOrderList;
    // Check for empty tree
    if (root == NULL)
        return postOrderList;
    stack<Node*> S;
    S.push(root);
    Node* prev = NULL;
    while (!S.empty()) {
        auto current = S.top();
        /* go down the tree in search of a leaf an if so
           process it and pop stack otherwise move down */
        if (prev == NULL || prev->left == current
            || prev->right == current) {
            if (current->left)
                S.push(current->left);
            else if (current->right)
                S.push(current->right);
            else {
                S.pop();
                postOrderList.push_back(current->data);
            }
            /* go up the tree from left node, if the child
               is right push it onto stack otherwise process
               parent and pop stack */
        }

        else if (current->left == prev) {
            if (current->right)
                S.push(current->right);
            else {
                S.pop();
                postOrderList.push_back(current->data);
            }

            /* go up the tree from right node and after
            coming back from right node process parent and
            pop stack */
        }
        else if (current->right == prev) {
            S.pop();
            postOrderList.push_back(current->data);
        }
        prev = current;
    }
    return postOrderList;
}

// Driver program to test above functions
int main()
{
    // Let us construct the tree shown in above figure
    struct Node* root = NULL;
    root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(4);
    root->left->right = newNode(5);
    root->right->left = newNode(6);
    root->right->right = newNode(7);
    printf("Post order traversal of binary tree is :\n");
    printf("[");
    vector<int> postOrderList = postOrderIterative(root);
    for (auto it : postOrderList)
        cout << it << " ";
    printf("]");
    return 0;
}

// This code is contributed by Aditya Kumar (adityakumar129)

C

// C program for iterative postorder traversal using one
// stack
#include <stdio.h>
#include <stdlib.h>

// Maximum stack size
#define MAX_SIZE 100

// A tree node
struct Node {
    int data;
    struct Node *left, *right;
};

// Stack type
struct Stack {
    int size;
    int top;
    struct Node** array;
};

// A utility function to create a new tree node
struct Node* newNode(int data)
{
    struct Node* node
        = (struct Node*)malloc(sizeof(struct Node));
    node->data = data;
    node->left = node->right = NULL;
    return node;
}

// A utility function to create a stack of given size
struct Stack* createStack(int size)
{
    struct Stack* stack
        = (struct Stack*)malloc(sizeof(struct Stack));
    stack->size = size;
    stack->top = -1;
    stack->array = (struct Node**)malloc(
        stack->size * sizeof(struct Node*));
    return stack;
}

// BASIC OPERATIONS OF STACK
int isFull(struct Stack* stack)
{
    return stack->top - 1 == stack->size;
}

int isEmpty(struct Stack* stack)
{
    return stack->top == -1;
}

void push(struct Stack* stack, struct Node* node)
{
    if (isFull(stack))
        return;
    stack->array[++stack->top] = node;
}

struct Node* pop(struct Stack* stack)
{
    if (isEmpty(stack))
        return NULL;
    return stack->array[stack->top--];
}

struct Node* peek(struct Stack* stack)
{
    if (isEmpty(stack))
        return NULL;
    return stack->array[stack->top];
}

// An iterative function to do postorder traversal of a
// given binary tree
void postOrderIterative(struct Node* root)
{
    // Check for empty tree
    if (root == NULL)
        return;

    struct Stack* stack = createStack(MAX_SIZE);
    do {
        // Move to leftmost node
        while (root) {
            // Push root's right child and then root to
            // stack.
            if (root->right)
                push(stack, root->right);
            push(stack, root);

            // Set root as root's left child
            root = root->left;
        }

        // Pop an item from stack and set it as root
        root = pop(stack);

        // If the popped item has a right child and the
        // right child is not processed yet, then make sure
        // right child is processed before root
        if (root->right && peek(stack) == root->right) {
            pop(stack); // remove right child from stack
            push(stack, root); // push root back to stack
            root = root->right; // change root so that the
                                // right child is processed
                                // next
        }
        else // Else print root's data and set root as NULL
        {
            printf("%d ", root->data);
            root = NULL;
        }
    } while (!isEmpty(stack));
}

// Driver program to test above functions
int main()
{
    // Let us construct the tree shown in above figure
    struct Node* root = NULL;
    root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(4);
    root->left->right = newNode(5);
    root->right->left = newNode(6);
    root->right->right = newNode(7);
    printf("Post order traversal of binary tree is :\n");
    printf("[");
    postOrderIterative(root);
    printf("]");

    return 0;
}

// This code is contributed by Aditya Kumar (adityakumar129)

Java

// A java program for iterative postorder traversal using
// stack

import java.util.ArrayList;
import java.util.Stack;

// A binary tree node
class Node {
    int data;
    Node left, right;

    Node(int item)
    {
        data = item;
        left = right;
    }
}

class BinaryTree {
    Node root;
    ArrayList<Integer> list = new ArrayList<Integer>();

    // An iterative function to do postorder traversal
    // of a given binary tree
    ArrayList<Integer> postOrderIterative(Node node)
    {
        Stack<Node> S = new Stack<Node>();

        // Check for empty tree
        if (node == null)
            return list;
        S.push(node);
        Node prev = null;
        while (!S.isEmpty()) {
            Node current = S.peek();

            /* go down the tree in search of a leaf an if so
            process it and pop stack otherwise move down */
            if (prev == null || prev.left == current || prev.right == current) {
                if (current.left != null)
                    S.push(current.left);
                else if (current.right != null)
                    S.push(current.right);
                else {
                    S.pop();
                    list.add(current.data);
                }

                /* go up the tree from left node, if the
                child is right push it onto stack otherwise
                process parent and pop stack */
            }
            else if (current.left == prev) {
                if (current.right != null)
                    S.push(current.right);
                else {
                    S.pop();
                    list.add(current.data);
                }

                /* go up the tree from right node and after
                coming back from right node process parent
                and pop stack */
            }
            else if (current.right == prev) {
                S.pop();
                list.add(current.data);
            }

            prev = current;
        }

        return list;
    }

    // Driver program to test above functions
    public static void main(String args[])
    {
        BinaryTree tree = new BinaryTree();

        // Let us create trees shown in above diagram
        tree.root = new Node(1);
        tree.root.left = new Node(2);
        tree.root.right = new Node(3);
        tree.root.left.left = new Node(4);
        tree.root.left.right = new Node(5);
        tree.root.right.left = new Node(6);
        tree.root.right.right = new Node(7);

        ArrayList<Integer> mylist = tree.postOrderIterative(tree.root);

        System.out.println(
            "Post order traversal of binary tree is :");
        System.out.println(mylist);
    }
}

// This code is contributed by Aditya Kumar (adityakumar129)

Python3

# Python3 program for iterative postorder traversal
# using one stack

# Stores the answer
ans = []

# A Binary tree node
class Node:

    # Constructor to create a new node
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

def peek(stack):
    if len(stack) > 0:
        return stack[-1]
    return None
# A iterative function to do postorder traversal of
# a given binary tree
def postOrderIterative(root):

    # Check for empty tree
    if root is None:
        return

    stack = []

    while(True):

        while (root):
            # Push root's right child and then root to stack
            if root.right is not None:
                stack.append(root.right)
            stack.append(root)

            # Set root as root's left child
            root = root.left

        # Pop an item from stack and set it as root
        root = stack.pop()

        # If the popped item has a right child and the
        # right child is not processed yet, then make sure
        # right child is processed before root
        if (root.right is not None and
            peek(stack) == root.right):
            stack.pop() # Remove right child from stack
            stack.append(root) # Push root back to stack
            root = root.right # change root so that the
                            # right childis processed next

        # Else print root's data and set root as None
        else:
            ans.append(root.data)
            root = None

        if (len(stack) <= 0):
                break

# Driver program to test above function
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)

print("Post Order traversal of binary tree is")
postOrderIterative(root)
print(ans)

# This code is contributed by Nikhil Kumar Singh(nickzuck_007)

C#

// A C# program for iterative postorder traversal using stack
using System;
using System.Collections.Generic;

// A binary tree node
class Node
{
  public int data;
  public Node left, right;

  public Node(int item)
  {
    data = item;
    left = right;
  }
}

public class BinaryTree
{
  Node root;
  List<int> list = new List<int>();

  // An iterative function to do postorder traversal
  // of a given binary tree
  List<int> postOrderIterative(Node node)
  {
    Stack<Node> S = new Stack<Node>();

    // Check for empty tree
    if (node == null)
      return list;
    S.Push(node);
    Node prev = null;
    while (S.Count != 0)
    {
      Node current = S.Peek();

      /* go down the tree in search of a leaf an if so process it
            and pop stack otherwise move down */
      if (prev == null || prev.left == current ||
          prev.right == current)
      {
        if (current.left != null)
          S.Push(current.left);
        else if (current.right != null)
          S.Push(current.right);
        else
        {
          S.Pop();
          list.Add(current.data);
        }

        /* go up the tree from left node, if the child is right
                push it onto stack otherwise process parent and pop
                stack */
      }
      else if (current.left == prev)
      {
        if (current.right != null)
          S.Push(current.right);
        else
        {
          S.Pop();
          list.Add(current.data);
        }

        /* go up the tree from right node and after coming back
                from right node process parent and pop stack */
      }
      else if (current.right == prev)
      {
        S.Pop();
        list.Add(current.data);
      }

      prev = current;
    }

    return list;
  }

  // Driver code
  public static void Main(String []args)
  {
    BinaryTree tree = new BinaryTree();

    // Let us create trees shown in above diagram
    tree.root = new Node(1);
    tree.root.left = new Node(2);
    tree.root.right = new Node(3);
    tree.root.left.left = new Node(4);
    tree.root.left.right = new Node(5);
    tree.root.right.left = new Node(6);
    tree.root.right.right = new Node(7);

    List<int> mylist = tree.postOrderIterative(tree.root);

    Console.WriteLine("Post order traversal of binary tree is :");
    foreach(int i in mylist)
      Console.Write(i+" ");
  }
}

// This code contributed by shikhasingrajput

Javascript

<script>
// A javascript program for iterative postorder traversal using stack

// A binary tree node
    class Node
    {
        constructor(item)
        {
            this.data=item;
            this.left=null;
            this.right=null;
        }
    }

    let root;
    let list = [];

    // An iterative function to do postorder traversal
    // of a given binary tree
    function postOrderIterative(node)
    {
        let S = [];
        // Check for empty tree
        if (node == null)
            return list;
        S.push(node);
        let prev = null;
        while (S.length!=0)
        {
            let current = S[S.length-1];

            /* go down the tree in search of a leaf an if so process it
            and pop stack otherwise move down */
            if (prev == null || prev.left == current ||
                                        prev.right == current)
            {
                if (current.left != null)
                    S.push(current.left);
                else if (current.right != null)
                    S.push(current.right);
                else
                {
                    S.pop();
                    list.push(current.data);
                }

                /* go up the tree from left node, if the child is right
                push it onto stack otherwise process parent and pop
                stack */
            }
            else if (current.left == prev)
            {
                if (current.right != null)
                    S.push(current.right);
                else
                {
                    S.pop();
                    list.push(current.data);
                }

                /* go up the tree from right node and after coming back
                from right node process parent and pop stack */
            }
            else if (current.right == prev)
            {
                S.pop();
                list.push(current.data);
            }

            prev = current;
        }

        return list;
    }

    // Driver program to test above functions

    // Let us create trees shown in above diagram
    root = new Node(1);
    root.left = new Node(2);
    root.right = new Node(3);
    root.left.left = new Node(4);
    root.left.right = new Node(5);
    root.right.left = new Node(6);
    root.right.right = new Node(7);

    let mylist = postOrderIterative(root);
    document.write("Post order traversal of binary tree is :<br>");
    for(let i = 0; i < mylist.length; i++)
    {
        document.write(mylist[i]+" ");
    }

    // This code is contributed by unknown2108
</script>

Output

Post order traversal of binary tree is :
[4 5 2 6 7 3 1 ]

Time Complexity: O(n)

Auxiliary Space: O(n)

Method 2:
Push directly root node two times while traversing to the left. While popping if you find stack top() is same as root then go for root->right else print root.

C++

// C++ program for iterative postorder traversal using one
// stack
#include <bits/stdc++.h>
using namespace std;

// A tree node
struct Node {
    int data;
    struct Node *left, *right;
};

// A utility function to create a new tree node
struct Node* newNode(int data)
{
    struct Node* node = new Node;
    node->data = data;
    node->left = node->right = NULL;
    return node;
}

// An iterative function to do postorder traversal of a
// given binary tree
vector<int> postOrderIterative(struct Node* root)
{
    vector<int> postOrderList;
    stack<Node*> st;
    while (true) {
        while (root) {
            st.push(root);
            st.push(root);
            root = root->left;
        }
        if (st.empty())
            return postOrderList;
        root = st.top();
        st.pop();
        if (!st.empty() && st.top() == root)
            root = root->right;
        else {
            postOrderList.push_back(root->data);
            root = NULL;
        }
    }
    return postOrderList;
}

// Driver program to test above functions
int main()
{
    // Let us construct the tree shown in above figure
    struct Node* root = NULL;
    root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(4);
    root->left->right = newNode(5);
    root->right->left = newNode(6);
    root->right->right = newNode(7);
    printf("Post order traversal of binary tree is :\n");
    printf("[");
    vector<int> postOrderList = postOrderIterative(root);
    for (auto it : postOrderList)
        cout << it << " ";
    printf("]");
    return 0;
}

// This code is contributed by Sania Kumari Gupta
// (kriSania804)

Java

// Simple Java program to print PostOrder Traversal(Iterative)
import java.util.Stack;

// A binary tree node
class Node
{
    int data;
    Node left, right;

    Node(int item)
    {
        data = item;
        left = right;
    }
}

// create a postorder class
class PostOrder
{
    Node root;

    // An iterative function to do postorder traversal
    // of a given binary tree
    private void postOrderIterative(Node root) {
        Stack<Node> stack = new Stack<>();
        while(true) {
            while(root != null) {
                stack.push(root);
                stack.push(root);
                root = root.left;
            }

            // Check for empty stack
            if(stack.empty()) return;
            root = stack.pop();

            if(!stack.empty() && stack.peek() == root) root = root.right;

            else {

                System.out.print(root.data + " "); root = null;
            }
        }
    }

    // Driver program to test above functions
    public static void main(String args[])
    {
    PostOrder tree = new PostOrder();

        // Let us create trees shown in above diagram
        tree.root = new Node(1);
        tree.root.left = new Node(2);
        tree.root.right = new Node(3);
        tree.root.left.left = new Node(4);
        tree.root.left.right = new Node(5);
        tree.root.right.left = new Node(6);
        tree.root.right.right = new Node(7);
        System.out.println("Post order traversal of binary tree is :");
        tree.postOrderIterative(tree.root);
    }
}

Python3

# Simple Python3 program to print
# PostOrder Traversal(Iterative)

# A binary tree node
class Node:

    def __init__(self, x):

        self.data = x
        self.right = None
        self.left = None

# Create a postorder class

# An iterative function to do postorder
# traversal of a given binary tree
def postOrderIterative(root):

    stack = []

    while(True):
        while(root != None):
            stack.append(root)
            stack.append(root)
            root = root.left

        # Check for empty stack
        if (len(stack) == 0):
            return

        root = stack.pop()

        if (len(stack) > 0 and stack[-1] == root):
            root = root.right
        else:
            print(root.data, end = " ")
            root = None

# Driver code
if __name__ == '__main__':

    # Let us create trees shown
    # in above diagram
    root = Node(1)
    root.left = Node(2)
    root.right = Node(3)
    root.left.left = Node(4)
    root.left.right = Node(5)
    root.right.left = Node(6)
    root.right.right = Node(7)

    print("Post order traversal of binary tree is :")

    postOrderIterative(root)

# This code is contributed by mohit kumar 29

C#

// Simple C# program to print PostOrder Traversal(Iterative)
using System;
using System.Collections.Generic;

// A binary tree node
public
  class Node
  {
    public
      int data;
    public
      Node left, right;
    public
      Node(int item)
    {
      data = item;
      left = right;
    }
  }

// create a postorder class
public class PostOrder
{
  Node root;

  // An iterative function to do postorder traversal
  // of a given binary tree
  private void postOrderIterative(Node root)
  {
    Stack<Node> stack = new Stack<Node>();
    while(true)
    {
      while(root != null)
      {
        stack.Push(root);
        stack.Push(root);
        root = root.left;
      }

      // Check for empty stack
      if(stack.Count == 0) return;
      root = stack.Pop();
      if(stack.Count != 0 && stack.Peek() == root) root = root.right;
      else
      {
        Console.Write(root.data + " "); root = null;
      }
    }
  }

  // Driver program to test above functions
  public static void Main(String []args)
  {
    PostOrder tree = new PostOrder();

    // Let us create trees shown in above diagram
    tree.root = new Node(1);
    tree.root.left = new Node(2);
    tree.root.right = new Node(3);
    tree.root.left.left = new Node(4);
    tree.root.left.right = new Node(5);
    tree.root.right.left = new Node(6);
    tree.root.right.right = new Node(7);
    Console.WriteLine("Post order traversal of binary tree is :");
    tree.postOrderIterative(tree.root);
  }
}

// This code is contributed by Rajput-Ji

Javascript

<script>

      // Simple JavaScript program to print
      // PostOrder Traversal(Iterative)

      // A binary tree node
      class Node {
        constructor(item) {
          this.data = item;
          this.left = null;
          this.right = null;
        }
      }

      // create a postorder class
      class PostOrder {
        constructor() {
          this.root = null;
        }
        // An iterative function to do postorder traversal
        // of a given binary tree
        postOrderIterative(root) {
          var stack = [];
          while (true) {
            while (root != null) {
              stack.push(root);
              stack.push(root);
              root = root.left;
            }

            // Check for empty stack
            if (stack.length == 0) return;
            root = stack.pop();
            if (stack.length != 0 && stack[stack.length - 1] == root)
              root = root.right;
            else {
              document.write(root.data + " ");
              root = null;
            }
          }
        }
      }
      // Driver program to test above functions
      var tree = new PostOrder();

      // Let us create trees shown in above diagram
      tree.root = new Node(1);
      tree.root.left = new Node(2);
      tree.root.right = new Node(3);
      tree.root.left.left = new Node(4);
      tree.root.left.right = new Node(5);
      tree.root.right.left = new Node(6);
      tree.root.right.right = new Node(7);
      document.write("Post order traversal of binary tree is :<br>");
      tree.postOrderIterative(tree.root);

</script>

Output

Post order traversal of binary tree is :
4 5 2 6 7 3 1 

Time Complexity: O(n)

Auxiliary Space: O(n)

Method 3 (Iterative PostOrder Traversal Using Stack and Hashing) :  

• Create a Stack for finding the postorder traversal and an unordered map for hashing to mark the visited nodes.
• Initially push the root node in the stack and follow the below steps until the stack is not empty. The stack will get empty when postorder traversal is stored in our answer container data structure.
• Mark the current node (node on the top of stack) as visited in our hashtable.
• If the left child of the current node is not NULL and not visited then push it into the stack.
• Otherwise, if the right child of the top node is not NULL and not visited push it into the stack
• If none of the above two conditions holds true then add the value of the current node to our answer and remove(pop) the current node from the stack.
• When the stack gets empty, we will have postorder traversal stored in our answer data structure (array or vector).

C++

// A C++ program for iterative postorder traversal using
// stack
#include <bits/stdc++.h>
using namespace std;
#define MAX_HEIGHT 100000

// Tree Node
struct Node {
    int data;
    Node* left;
    Node* right;
};

// Utility function to create a new Tree Node
Node* newNode(int val)
{
    Node* temp = new Node;
    temp->data = val;
    temp->left = NULL;
    temp->right = NULL;

    return temp;
}

// Function to Build Tree
Node* buildTree(string str)
{
    // Corner Case
    if (str.length() == 0 || str[0] == 'N')
        return NULL;

    // Creating vector of strings from input
    // string after splitting by space
    vector<string> ip;

    istringstream iss(str);
    for (string str; iss >> str;)
        ip.push_back(str);

    // Create the root of the tree
    Node* root = newNode(stoi(ip[0]));

    // Push the root to the queue
    queue<Node*> queue;
    queue.push(root);

    // Starting from the second element
    int i = 1;
    while (!queue.empty() && i < ip.size()) {

        // Get and remove the front of the queue
        Node* currNode = queue.front();
        queue.pop();

        // Get the current node's value from the string
        string currVal = ip[i];

        // If the left child is not null
        if (currVal != "N") {

            // Create the left child for the current node
            currNode->left = newNode(stoi(currVal));

            // Push it to the queue
            queue.push(currNode->left);
        }

        // For the right child
        i++;
        if (i >= ip.size())
            break;
        currVal = ip[i];

        // If the right child is not null
        if (currVal != "N") {

            // Create the right child for the current node
            currNode->right = newNode(stoi(currVal));

            // Push it to the queue
            queue.push(currNode->right);
        }
        i++;
    }

    return root;
}

// An iterative function to do postorder traversal
// of a given binary tree
vector<int> postOrder(Node* node)
{
    stack<Node*> s;

    // vector to store the postorder traversal
    vector<int> post;

    // Using unordered map as hash table for hashing to mark
    // the visited nodes
    unordered_map<Node*, int> vis;

    // push the root node in the stack to traverse the tree
    s.push(node);

    // stack will be empty when traversal is completed
    while (!s.empty()) {

        // mark the node on the top of stack as visited
        vis[s.top()] = 1;

        // if left child of the top node is not NULL and not
        // visited push it into the stack
        if (s.top()->left != 0) {
            if (!vis[s.top()->left]) {
                s.push(s.top()->left);
                continue;
            }
        }

        // Otherwise if the right child of the top node is
        // not NULL and not visited push it into the stack
        if (s.top()->right != 0) {
            if (!vis[s.top()->right]) {
                s.push(s.top()->right);
                continue;
            }
        }

        // Add the value of the top node in our postorder
        // traversal answer if none of the above two
        // conditions are met
        post.push_back(s.top()->data);

        // Remove the top node from the stack
        s.pop();
    }

    // post will now contain the postorder traversal of the
    // tree
    return post;
}

int main()
{
    // Constructing the tree as shown in above diagram
    string s = "1 2 3 4 5 6 7";
    Node* root = buildTree(s);

    vector<int> ans;

    ans = postOrder(root);

    cout << "Post order traversal of binary tree is :\n";
    for (int i = 0; i < ans.size(); i++)
        cout << ans[i] << " ";

    cout << endl;

    return 0;
}

// This code is contributed by Ishan Khandelwal

Java

// Simple Java program to print PostOrder Traversal(Iterative)
import java.util.Stack;

// A binary tree node
class Node
{
    int data;
    Node left, right;

    Node(int item)
    {
        data = item;
        left = right;
    }
}

// create a postorder class
class PostOrder
{
    Node root;

    // An iterative function to do postorder traversal
    // of a given binary tree
    private void postOrderIterative(Node root) {
        Stack<Node> stack = new Stack<>();
        while(true) {
            while(root != null) {
                stack.push(root);
                stack.push(root);
                root = root.left;
            }

            // Check for empty stack
            if(stack.empty()) return;
            root = stack.pop();

            if(!stack.empty() && stack.peek() == root) root = root.right;

            else {

                System.out.print(root.data + " "); root = null;
            }
        }
    }

    // Driver program to test above functions
    public static void main(String args[])
    {
    PostOrder tree = new PostOrder();

        // Let us create trees shown in above diagram
        tree.root = new Node(1);
        tree.root.left = new Node(2);
        tree.root.right = new Node(3);
        tree.root.left.left = new Node(4);
        tree.root.left.right = new Node(5);
        tree.root.right.left = new Node(6);
        tree.root.right.right = new Node(7);
        System.out.println("Post order traversal of binary tree is :");
        tree.postOrderIterative(tree.root);
    }
}

// This code is contributed by ishankhandelwals.

Python3

# Simple Python3 program to print
# PostOrder Traversal(Iterative)

# A binary tree node
class Node:

    def __init__(self, x):

        self.data = x
        self.right = None
        self.left = None

# Create a postorder class

# An iterative function to do postorder
# traversal of a given binary tree
def postOrderIterative(root):

    stack = []

    while(True):
        while(root != None):
            stack.append(root)
            stack.append(root)
            root = root.left

        # Check for empty stack
        if (len(stack) == 0):
            return

        root = stack.pop()

        if (len(stack) > 0 and stack[-1] == root):
            root = root.right
        else:
            print(root.data, end=" ")
            root = None

# Driver code
if __name__ == '__main__':

    # Let us create trees shown
    # in above diagram
    root = Node(1)
    root.left = Node(2)
    root.right = Node(3)
    root.left.left = Node(4)
    root.left.right = Node(5)
    root.right.left = Node(6)
    root.right.right = Node(7)

    print("Post order traversal of binary tree is :")

    postOrderIterative(root)

    # This code is contributed by ishankhandelwals.

C#

// Simple C# program to print PostOrder Traversal(Iterative)
using System;
using System.Collections.Generic;

// A binary tree node
public class Node {
  public int data;
  public Node left, right;
  public Node(int item)
  {
    data = item;
    left = right;
  }
}

// create a postorder class
public class PostOrder {
  Node root;

  // An iterative function to do postorder traversal
  // of a given binary tree
  private void postOrderIterative(Node root)
  {
    Stack<Node> stack = new Stack<Node>();
    while (true) {
      while (root != null) {
        stack.Push(root);
        stack.Push(root);
        root = root.left;
      }

      // Check for empty stack
      if (stack.Count == 0)
        return;
      root = stack.Pop();
      if (stack.Count != 0 && stack.Peek() == root)
        root = root.right;
      else {
        Console.Write(root.data + " ");
        root = null;
      }
    }
  }

  // Driver program to test above functions
  public static void Main(String[] args)
  {
    PostOrder tree = new PostOrder();

    // Let us create trees shown in above diagram
    tree.root = new Node(1);
    tree.root.left = new Node(2);
    tree.root.right = new Node(3);
    tree.root.left.left = new Node(4);
    tree.root.left.right = new Node(5);
    tree.root.right.left = new Node(6);
    tree.root.right.right = new Node(7);
    Console.WriteLine(
      "Post order traversal of binary tree is :");
    tree.postOrderIterative(tree.root);
  }
}

// This code is contributed by ishankhandelwals.

Javascript

      // Simple JavaScript program to print
      // PostOrder Traversal(Iterative)

      // A binary tree node
      class Node {
        constructor(item) {
          this.data = item;
          this.left = null;
          this.right = null;
        }
      }

      // create a postorder class
      class PostOrder {
        constructor() {
          this.root = null;
        }
        // An iterative function to do postorder traversal
        // of a given binary tree
        postOrderIterative(root) {
          var stack = [];
          while (true) {
            while (root != null) {
              stack.push(root);
              stack.push(root);
              root = root.left;
            }

            // Check for empty stack
            if (stack.length == 0) return;
            root = stack.pop();
            if (stack.length != 0 && stack[stack.length - 1] == root)
              root = root.right;
            else {
              console.log(root.data + " ");
              root = null;
            }
          }
        }
      }
      // Driver program to test above functions
      var tree = new PostOrder();

      // Let us create trees shown in above diagram
      tree.root = new Node(1);
      tree.root.left = new Node(2);
      tree.root.right = new Node(3);
      tree.root.left.left = new Node(4);
      tree.root.left.right = new Node(5);
      tree.root.right.left = new Node(6);
      tree.root.right.right = new Node(7);
      console.log("Post order traversal of binary tree is :<br>");
      tree.postOrderIterative(tree.root);

// This code is contributed by ishankhandelwals.

Output

Post order traversal of binary tree is :
4 5 2 6 7 3 1 

Time complexity: O(n) where n is no of nodes in a binary tree

Auxiliary Space: O(n)
This article is compiled by Aashish Barnwal. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above

Method 4:

• In this method, the node is only pushed once. 
• Travel to the extreme left using a loop until null. 
• Then loop again with the right of the top element of the stack(if it exists). The loop used for traversing to the extreme left is only used in this step in future. 
• If the right node is null, then pop until that sub-branch is popped from the stack(to avoid an infinite loop of continuously adding and popping the same thing).

The reason why this program works is that after traversing to extreme left in the beginning, further the program has two paths of execution. One is when the right node is given the control and the other is when the right node hits null. When the right node is given the control, just traverse to the extreme left. If null is hit, pop till that sub branch is eliminated from the stack. So a boolean variable is used so that when right node is given control, it sets to true and program changes to travel extreme left mode and other cases just keep on popping.

C++

// A C++ program for iterative postorder traversal using
// stack
#include <bits/stdc++.h>
using namespace std;
#define MAX_HEIGHT 100000

// Tree Node
struct Node {
  int data;
  Node* left;
  Node* right;
};

// Utility function to create a new Tree Node
Node* newNode(int val)
{
  Node* temp = new Node;
  temp->data = val;
  temp->left = NULL;
  temp->right = NULL;

  return temp;
}

// Function to Build Tree
Node* buildTree(string str)
{
  // Corner Case
  if (str.length() == 0 || str[0] == 'N')
    return NULL;

  // Creating vector of strings from input
  // string after splitting by space
  vector<string> ip;

  istringstream iss(str);
  for (string str; iss >> str;)
    ip.push_back(str);

  // Create the root of the tree
  Node* root = newNode(stoi(ip[0]));

  // Push the root to the queue
  queue<Node*> queue;
  queue.push(root);

  // Starting from the second element
  int i = 1;
  while (!queue.empty() && i < ip.size()) {

    // Get and remove the front of the queue
    Node* currNode = queue.front();
    queue.pop();

    // Get the current node's value from the string
    string currVal = ip[i];

    // If the left child is not null
    if (currVal != "N") {

      // Create the left child for the current node
      currNode->left = newNode(stoi(currVal));

      // Push it to the queue
      queue.push(currNode->left);
    }

    // For the right child
    i++;
    if (i >= ip.size())
      break;
    currVal = ip[i];

    // If the right child is not null
    if (currVal != "N") {

      // Create the right child for the current node
      currNode->right = newNode(stoi(currVal));

      // Push it to the queue
      queue.push(currNode->right);
    }
    i++;
  }

  return root;
}

// An iterative function to do postorder traversal
// of a given binary tree
vector<int> postOrder(Node* node)
{
  stack<Node*> s;

  // vector to store the postorder traversal
  vector<int> post;

  // Using unordered map as hash table for hashing to mark
  // the visited nodes
  unordered_map<Node*, int> vis;

  // push the root node in the stack to traverse the tree
  s.push(node);

  // stack will be empty when traversal is completed
  while (!s.empty()) {

    // mark the node on the top of stack as visited
    vis[s.top()] = 1;

    // if left child of the top node is not NULL and not
    // visited push it into the stack
    if (s.top()->left != 0) {
      if (!vis[s.top()->left]) {
        s.push(s.top()->left);
        continue;
      }
    }

    // Otherwise if the right child of the top node is
    // not NULL and not visited push it into the stack
    if (s.top()->right != 0) {
      if (!vis[s.top()->right]) {
        s.push(s.top()->right);
        continue;
      }
    }

    // Add the value of the top node in our postorder
    // traversal answer if none of the above two
    // conditions are met
    post.push_back(s.top()->data);

    // Remove the top node from the stack
    s.pop();
  }

  // post will now contain the postorder traversal of the
  // tree
  return post;
}

int main()
{
  // Constructing the tree as shown in above diagram
  string s = "1 2 3 4 5 6 7";
  Node* root = buildTree(s);

  vector<int> ans;

  ans = postOrder(root);

  cout << "Post order traversal of binary tree is :\n";
  for (int i = 0; i < ans.size(); i++)
    cout << ans[i] << " ";

  cout << endl;

  return 0;
}

// This code is contributed by ishankhandelwals.

Java

// Simple Java program to print PostOrder Traversal(Iterative)
import java.util.Arrays;
import java.util.Stack;

public class GFG {
    public static void main (String[] args) {
        //Constructing the Binary Tree by assigning the right and left
        //to each nodes
        //The Node structure of Binary Tree is defined below.
        Node root = new Node(1);
        root.left = new Node(2);
        root.right = new Node(3);
        root.left.left = new Node(4);
        root.left.right = new Node(5);
        root.right.left = new Node(6);
        root.right.right = new Node(7);
        postorder_iterative(root);
    }
    public static void postorder_iterative(Node root){
        //The stack to store nodes
        Stack<Node> s = new Stack<>();
        //This check is used to check whether the traversal is from the top element
        //to it's right. Only then this will be true to invoke the inside while
        //loop
        boolean check = true;
        //Beginning an infinite loop
        while(true){
            //This loop traverses to extreme left node.
            while(root != null && check){
                s.push(root);
                root = root.left;
            }
            //If the stack is empty, the traversal is finished
            if(s.empty()) break;
            //To avoid infinite looping this check is necessary
            //The node of previous iteration is stored in root, so if right
            //is already visited it won't execute. Hence popping that subtree
            //to avoid infinite looping.
            if(root != s.peek().right){
                root = s.peek().right;
                check = true;
                continue;
            }
            //If the node wasn't in any of the special cases above, just pop and
            //print the value
            root = s.pop();
            System.out.print(root.value + " ");
            check = false;
        }
    }
}
//Binary Tree Node Structure
class Node{
    int value;
    Node left, right;
    public Node(int value){
        this.value = value;
        left = right = null;
    }
}
//This code is contributed by Ritvik Saran S

Python

# Python3 program to print the
# PostOrder Traversal(Iterative)

# Binary tree node structure
class Node:

    def __init__(self, x):

        self.data = x
        self.right = None
        self.left = None

# An iterative function to do postorder
# traversal of a given binary tree
def postOrderIterative(root):

    stack = []
    check = True

    while(True):
        while(root != None):
            stack.append(root)
            root = root.left

        # If the stack is empty, the traversal is finished
        if (len(stack) == 0):
            return
        #To avoid infinite looping this check is necessary
        if (root != stack[-1].right):
          root = stack[-1].right
          check = True
          continue

        root = stack.pop()
        print(root.data, end = " ")
        check = False

# Driver code
if __name__ == '__main__':

    # Let us create trees shown
    # in above diagram
    root = Node(1)
    root.left = Node(2)
    root.right = Node(3)
    root.left.left = Node(4)
    root.left.right = Node(5)
    root.right.left = Node(6)
    root.right.right = Node(7)

    print("Post order traversal of binary tree is :")

    postOrderIterative(root)
#This code is contributed by Ritvik Saran S

C#

// C# program to print PostOrder Traversal(Iterative)
using System;
using System.Collections.Generic;

// Binary tree node structure
public class Node {
    public int data;
    public Node left, right;
    public Node(int item)
    {
        data = item;
        left = right;
    }
}

// Postorder class
public class PostOrder {
    Node root;

    // Iterative function to do postorder traversal
    private void postOrderIterative(Node root)
    {
        Stack<Node> stack = new Stack<Node>();
        // This check is used to check whether the traversal
        // is from the top element to it's right. Only then
        // this will be true to invoke the inside while loop
        bool check = true;
        // Beginning an infinite loop
        while (true) {
            // This loop traverses to extreme left node.
            while (root != null && check) {
                stack.Push(root);
                root = root.left;
            }

            // If the stack is empty, the traversal is
            // finished
            if (stack.Count == 0)
                return;
            // To avoid infinite looping this check is
            // necessary The node of previous iteration is
            // stored in root, so if right is already visited
            // it won't execute. Hence popping that subtree
            // to avoid infinite looping.
            if (root != stack.Peek().right) {
                root = stack.Peek().right;
                check = true;
                continue;
            }
            // If the node wasn't in any of the special
            // cases above, just pop and print the value
            root = stack.Pop();
            Console.Write(root.data + " ");
            check = false;
        }
    }

    // Driver program to test above functions
    public static void Main(String[] args)
    {
        PostOrder tree = new PostOrder();

        // Let us create trees shown in above diagram
        tree.root = new Node(1);
        tree.root.left = new Node(2);
        tree.root.right = new Node(3);
        tree.root.left.left = new Node(4);
        tree.root.left.right = new Node(5);
        tree.root.right.left = new Node(6);
        tree.root.right.right = new Node(7);
        Console.WriteLine(
            "Post order traversal of the binary tree is :");
        tree.postOrderIterative(tree.root);
    }
}
// This code is contributed by Ritvik Saran S

Javascript

// Simple JavaScript program to print
// PostOrder Traversal(Iterative)

// A binary tree node
class Node {
  constructor(item) {
    this.data = item;
    this.left = null;
    this.right = null;
  }
}

// create a postorder class
class PostOrder {
  constructor() {
    this.root = null;
  }

  // An iterative function to do postorder traversal
  // of a given binary tree
  postOrderIterative(root) {
    var stack = [];
    while (true) {
      while (root != null) {
        stack.push(root);
        stack.push(root);
        root = root.left;
      }

      // Check for empty stack
      if (stack.length == 0) return;
      root = stack.pop();
      if (stack.length != 0 && stack[stack.length - 1] == root)
        root = root.right;
      else {
        console.log(root.data + " ");
        root = null;
      }
    }
  }
}

// Driver program to test above functions
var tree = new PostOrder();

// Let us create trees shown in above diagram
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(6);
tree.root.right.right = new Node(7);
console.log("Post order traversal of binary tree is :<br>");
tree.postOrderIterative(tree.root);

// This code is contributed by ishankhandelwals.

Output

4 5 2 6 7 3 1 

Time Complexity: O(n), n is the number of nodes of the tree.

Auxiliary Space: O(n), extra stack space is used.