Iterative Method to find Height of Binary Tree
Last Updated :
21 Jun, 2022
There are two conventions to define the height of a Binary Tree
- Number of nodes on the longest path from the root to the deepest node.
- Number of edges on the longest path from the root to the deepest node.
In this post, the first convention is followed. For example, the height of the below tree is 3.
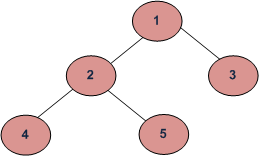
The recursive method to find the height of the Binary Tree is discussed here. How to find height without recursion? We can use level order traversal to find height without recursion. The idea is to traverse level by level. Whenever move down to a level, increment height by 1 (height is initialized as 0). Count number of nodes at each level, stop traversing when the count of nodes at the next level is 0.
Following is a detailed algorithm to find level order traversal using a queue.
Create a queue.
Push root into the queue.
height = 0
nodeCount = 0 // Number of nodes in the current level.
// If the number of nodes in the queue is 0, it implies
// that all the levels of the tree have been parsed. So,
// return the height. Otherwise count the number of nodes
// in the current level and push the children of all the
// nodes in the current level to the queue.
Loop
nodeCount = size of queue
// If the number of nodes at this level is 0, return height
if nodeCount is 0
return Height;
else
increase Height
// Remove nodes of this level and add nodes of
// next level
while (nodeCount > 0)
push its children to queue
pop node from front
decrease nodeCount
// At this point, queue has nodes of next level
Following is the implementation of the above algorithm.
C++
#include <iostream>
#include <queue>
using namespace std;
class Node {
public:
int data;
Node* left;
Node* right;
};
Node* createNode(int data)
{
Node* newnode = new Node();
newnode->data = data;
newnode->left = NULL;
newnode->right = NULL;
return newnode;
}
int calculateHeight(Node* root)
{
queue<Node*> nodesInLevel;
int height = 0;
int nodeCount = 0;
Node* currentNode;
if (root == NULL) {
return 0;
}
nodesInLevel.push(root);
while (!nodesInLevel.empty()) {
height++;
nodeCount = nodesInLevel.size();
while (nodeCount--) {
currentNode = nodesInLevel.front();
if (currentNode->left != NULL) {
nodesInLevel.push(currentNode->left);
}
if (currentNode->right != NULL) {
nodesInLevel.push(currentNode->right);
}
nodesInLevel.pop();
}
}
return height;
}
int main()
{
Node* root = NULL;
root = createNode(1);
root->left = createNode(2);
root->left->left = createNode(4);
root->left->right = createNode(5);
root->right = createNode(3);
cout << "The height of the binary tree using iterative "
"method is: " << calculateHeight(root) << ".";
return 0;
}
|
Java
import java.util.LinkedList;
import java.util.Queue;
class Node
{
int data;
Node left, right;
Node(int item)
{
data = item;
left = right;
}
}
class BinaryTree
{
Node root;
int treeHeight(Node node)
{
if (node == null)
return 0;
Queue<Node> q = new LinkedList();
q.add(node);
int height = 0;
while (1 == 1)
{
int nodeCount = q.size();
if (nodeCount == 0)
return height;
height++;
while (nodeCount > 0)
{
Node newnode = q.peek();
q.remove();
if (newnode.left != null)
q.add(newnode.left);
if (newnode.right != null)
q.add(newnode.right);
nodeCount--;
}
}
}
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
System.out.println("Height of tree is " + tree.treeHeight(tree.root));
}
}
|
Python3
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def treeHeight(root):
if root is None:
return 0
q = []
q.append(root)
height = 0
while(True):
nodeCount = len(q)
if nodeCount == 0 :
return height
height += 1
while(nodeCount > 0):
node = q[0]
q.pop(0)
if node.left is not None:
q.append(node.left)
if node.right is not None:
q.append(node.right)
nodeCount -= 1
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
print ("Height of tree is", treeHeight(root))
|
C#
using System;
using System.Collections.Generic;
class Node
{
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right;
}
}
public class BinaryTree
{
Node root;
int treeHeight(Node node)
{
if (node == null)
return 0;
Queue<Node> q = new Queue<Node>();
q.Enqueue(node);
int height = 0;
while (1 == 1)
{
int nodeCount = q.Count;
if (nodeCount == 0)
return height;
height++;
while (nodeCount > 0)
{
Node newnode = q.Peek();
q.Dequeue();
if (newnode.left != null)
q.Enqueue(newnode.left);
if (newnode.right != null)
q.Enqueue(newnode.right);
nodeCount--;
}
}
}
public static void Main(String []args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
Console.WriteLine("Height of tree is " +
tree.treeHeight(tree.root));
}
}
|
Javascript
<script>
class Node
{
constructor(item)
{
this.data = item;
this.left = this.right=null;
}
}
let root;
function treeHeight(node)
{
if (node == null)
return 0;
let q = [];
q.push(node);
let height = 0;
while (1 == 1)
{
let nodeCount = q.length;
if (nodeCount == 0)
return height;
height++;
while (nodeCount > 0)
{
let newnode = q.shift();
if (newnode.left != null)
q.push(newnode.left);
if (newnode.right != null)
q.push(newnode.right);
nodeCount--;
}
}
}
root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
document.write("Height of tree is " + treeHeight(root));
</script>
|
Output
The height of the binary tree using iterative method is: 3.
Time Complexity: O(n) where n is the number of nodes in a given binary tree.
Space Complexity: O(n) where n is the number of nodes in a given binary tree.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...