Is rolling a dice a probability distribution?

Probability of a set of events can be considered as a measure of the likelihood of an event to occur. There are many events that cannot be predicted with total certainty. The chance of the occurrence of any event can be predicted with the help of probability. The value of chance of occurrence or probability of occurrence of events lies between 0 to 1. The value of 0 indicates the occurrence of an impossible event and 1 to be a certain event. The probability of occurrence of all the events in a sample space adds up to 1.

For instance, on tossing a coin, we obtain either a Head Or Tail, there are only two of the possible outcomes (H, T). If we toss two coins, we can obtain three possibilities for the events to occur, that is, both the coins can show a combination of either heads or tails. The possible combinations are therefore obtained, i.e.(H, H), (H, T),(T, T).

Formula for Probability

The possibility of happening of an event is defined using the probability formula which is equivalent to the ratio of the number of favorable outcomes to the total number of outcomes.

Probability of event to happen,

P(E) = 

Rolling a die

The dice probability is the study of the chance of obtaining a specific number with one dice. The probability of occurrence of an event is by looking at the number of possible outcomes. In case of a dice, there are six total faces, and for any roll, there are six possible outcomes that can be obtained. 

Formula Used:

Probability =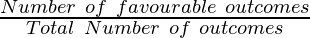 

For the odds of rolling a specific number (6, for example) on a dice, this gives:

Probability = 1/6 = 16.7

Probabilities are obtained in the form of numbers, between 0 (no chance) and 1 (certainty), but you can multiply this by 100 to get a percentage. 

Therefore, the chance of rolling a 6 on a single die is 16.7 percent.

Rolling Two or more dice

The following rule holds in the case of probability, 

Probability = Number of desired outcomes ÷ Number of possible outcomes. 

The total outcome possibilities are obtained by multiplying the number of sides on one die by the number of sides on the other. 

For instance, In order to obtain a total score of 4 on two dice, this can be achieved by rolling a 1 and 3, 2 and 2, or a 3 and 1. The order of occurrence of numbers on die are considered individually. 

For rolling a 4, there are three ways to get the outcome desired. In all, there are 36 possible outcomes. 

Probability =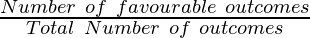 

As a percentage, this is 8.33 percent. For two dice, 7 is the most likely result, with six ways to achieve it.

Therefore, probability = 6 ÷ 36 = 0.167 = 16.7 percent.

Sample Questions

Question 1. Mallika rolled a dice then find the probability that Mallika will get a prime number on the dice?

Solution:

Here we have the,

Sample Space = S = (1,2,3,4,5,6)

Thus,

The total number of outcomes = n

n = 6

Assume

Event of getting a prime number be X

Then,

Number of favorable outcomes,

{2, 3, 5}

n(X) = 3

Where,

X  = 3

Now,

Probability, P(X) =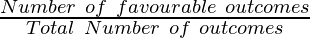 

= 3/6

= 1/2

Therefore,

Probability of getting a prime number on rolling a dice is 1/2.

Question 2. What is the probability of getting an even number when a dice is rolled?

Solution:

Here we have the,

Sample Space = S = (1,2,3,4,5,6)

Thus,

The total number of outcomes = n

n = 6

Assume

Event of getting a prime number be X

Then,

Number of favorable outcomes,

{2, 4, 6}

n(X) = 3

Where,

X  = 3

Now,

Probability, P(X) =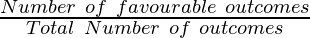 

= 3/6

= 1/2

Therefore,

Probability of getting an even number on rolling a dice is 1/2.

Question 3. If Yash throws a dice 300 times and gets the number 5, 50 times then find

• Probability of getting 5
• Probability of getting number under 5 

Solution:

Here,

• Probability of getting 5

Sample space = 50

Probability, P{Getting 5} =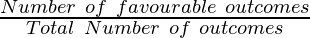 

P{Getting 5} = 50/300

P{Getting 5} = 1/6

• Probability of getting number under 5

The sample spaces, Assume X = 250

Probability, P{X} =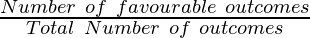 

P{X} = 250/300

P{X} = 5/6

Therefore,

Probability of getting a number under 5 is 5/6.

Question 4. If two dice a rolled together then find the probability of getting a sum equals to 8?

Solution:

Here we have the,

Sample space when two dice are rolled (S) =

{ (1,1),(1,2),(1,3),(1,4),(1,5),(1,6)

 (2,1),(2,2),(2,3),(2,4),(2,5),(2,6)

 (3,1),(3,2),(3,3),(3,4),(3,5),(3,6)

 (4,1),(4,2),(4,3),(4,4),(4,5),(4,6)

 (5,1),(5,2),(5,3),(5,4),(5,5),(5,6)

 (6,1),(6,2),(6,3),(6,4),(6,5),(6,6) }

Thus,

The total number of outcomes = n

n = 36

Assume that the X is the event of obtaining the sum of numbers on dices that is equal to 8.

Therefore,

There are 5 possible outcomes that are,

X = {(2,6), (3,5), (4,4), (5,3), (6,2)}

n(X) = 5

Now,

Probability, P(X) =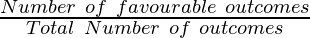 

P(X) = 5/36 = 5/36

Therefore,

Probability of getting a sum equal to 8 when two dices are rolled together is 5/36.