Inverse of Permutation Group
Last Updated :
22 Feb, 2021
Inverse of Permutation Group-: If the product of two permutations is the identical permutation then each of them is called inverse of each other.
For Example-: The permutations
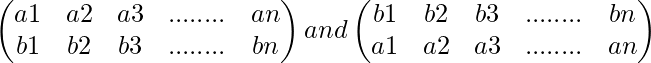
are inverse of each other since their product is 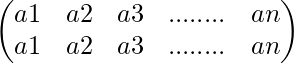
which is an identical permutation.
Example 1-: Find the inverse of permutation 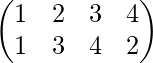
Solution-: Let the inverse of permutation be 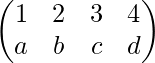 \
\
where a, b, c and d are to be calculated.
Then According to definition of Inverse of Permutation
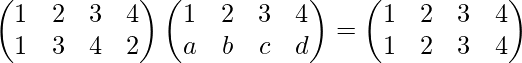
or 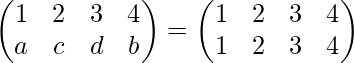
∴ b=4 , c=2 , a=1 , d=3
∴ Required inverse is 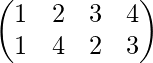
Example 2-: Calculate A-1 if A=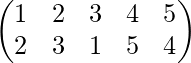
Solution-: Let the inverse of A be 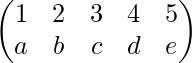
where a, b, c, d and e are to be calculated.
Then According to definition of Inverse of Permutation
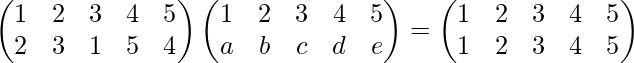
or 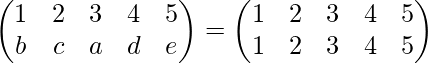
∴ b=1 , c=2 , a=3 , e=4 , d=5
∴ We have A-1= 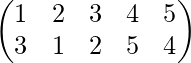
Example 3-: If 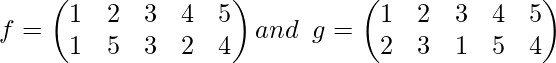
then compute f-1o g-1.
Solution-:
f-1=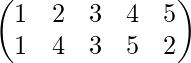
g-1=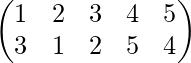
f-1o g-1= 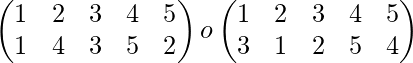
f-1o g-1=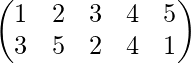
Example 4-: If P1=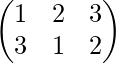 , P2=
, P2= 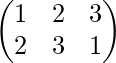 ,P3=
,P3=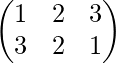
Find (P1 o P2)-1 and (P2 o P3)-1.
Solution-: P1 o P2= 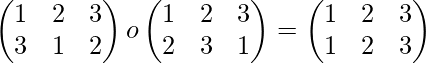
P2 o P3= 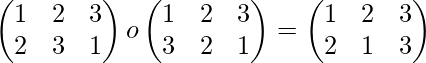
Also, we know that if P-1 be the inverse of permutation P, then P-1 o P = I .
∴ (P1 o P2)-1 = inverse of 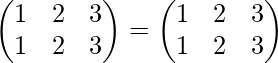
∴ (P2 o P3)-1 = inverse of 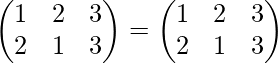
Example 5-: Prove that (1 2 3 ……. n )-1 = ( n n-1 n-3 ….. 2 1)
Solution-: ( 1 2 3 ….. n)= 
=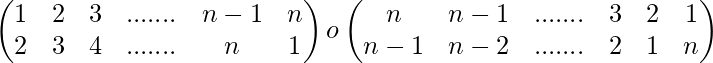
=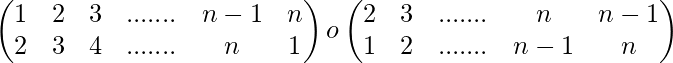
=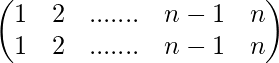 =I
=I
Hence, (1 2 3 ……. n )-1 = ( n n-1 n-3 ….. 2 1)
Share your thoughts in the comments
Please Login to comment...