Intuition behind Adagrad Optimizer

Adagrad stands for Adaptive Gradient Optimizer.  There were optimizers like Gradient Descent, Stochastic Gradient Descent, mini-batch SGD, all were used to reduce the loss function with respect to the weights. The weight updating formula is as follows:

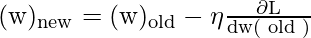
Based on iterations, this formula can be written as:

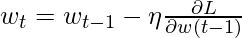
where

w(t) = value of w at current iteration, w(t-1) = value of w at previous iteration and η = learning rate.

In SGD and mini-batch SGD, the value of η used to be the same for each weight, or say for each parameter. Typically, η = 0.01.  But in Adagrad Optimizer the core idea is that each weight has a different learning rate (η). This modification has great importance, in the real-world dataset, some features are sparse (for example, in Bag of Words most of the features are zero so it’s sparse) and some are dense (most of the features will be noon-zero), so keeping the same value of learning rate for all the weights is not good for optimization. The weight updating formula for adagrad looks like:

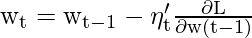
Where alpha(t) denotes different learning rates for each weight at each iteration. 

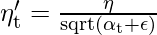
Here, η is a constant number, epsilon is a small positive value number to avoid divide by zero error if in case alpha(t) becomes 0 because if alpha(t) become zero then the learning rate will become zero which in turn after multiplying by derivative will make w(old) = w(new), and this will lead to small convergence.

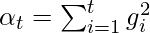
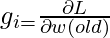
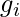is derivative of loss with respect to weight and 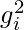will always be positive since its a square term, which means that alpha(t) will also remain positive, this implies that alpha(t) >= alpha(t-1).

It can be seen from the formula that as alpha(t) and 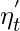is inversely proportional to one another, this implies that as alpha(t) will increase, 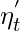will decrease. This means that as the number of iterations will increase, the learning rate will reduce adaptively, so you no need to manually select the learning rate.

Advantages of Adagrad:

• No manual tuning of the learning rate required.
• Faster convergence
• More reliable

One main disadvantage of Adagrad optimizer is that alpha(t) can become large as the number of iterations will increase and due to this 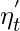will decrease at the larger rate. This will make the old weight almost equal to the new weight which may lead to slow convergence.