Introduction to Queue Automata
Last Updated :
08 Jul, 2020
We already know about Finite Automata which can be used to accept regular languages and Pushdown Automata that can be used to recognize Context Free Languages.
Queue Automata(QDA) is a non-deterministic automata that is similar to Pushdown Automata but has a queue instead of a stack which helps Queue automata to recognize languages beyond Context Free Languages.
A QDA is a 6 – tuple 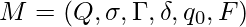
Where
- Q is the set of finite states.
 is the set of finite input alphabets.
is the set of finite input alphabets. is the set of finite queue alphabets.
is the set of finite queue alphabets.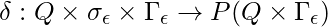 .
.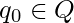 is the start state.
is the start state.- F
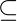 Q is the set of accept states.
Q is the set of accept states.
Acceptance of a string
A QDA 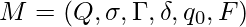 accepts input
accepts input 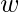 if
if 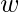 can be written as
can be written as 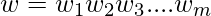 , where each
, where each 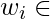
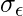 and there are states
and there are states  and strings
and strings  exist, such that they satisfy the following conditions:
exist, such that they satisfy the following conditions:
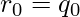 and
and 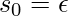 .
.- For

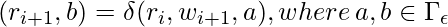 and
and 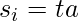 and
and 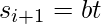 and
and 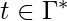
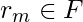
Example:
Define the queue automata for language 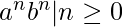 Solution:
Q = {q0, q1, q2, q3} and
Solution:
Q = {q0, q1, q2, q3} and 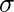 ={a, b} and
={a, b} and 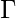 = {a, b, $}
And the transition functions are given by:
= {a, b, $}
And the transition functions are given by:
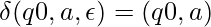
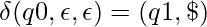
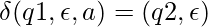
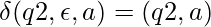
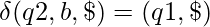
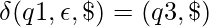
 Let us see how this automata works for aabb.
Let us see how this automata works for aabb.
| Row |
State |
Input |
Transition function |
Queue(Input from left) |
State after move |
| 1 |
q0 |
aabb |
δ(q0, a, ε)={(q0, a)} |
a |
q0 |
| 2 |
q0 |
aabb |
δ(q0, a, ε)={(q0, a)} |
aa |
q0 |
| 3 |
q0 |
ε |
δ(q0, ε, ε)={(q1, $)} |
$aa |
q1 |
| 4 |
q1 |
ε |
δ(q1, ε, a)={(q2, ε)} |
$a |
q2 |
| 5 |
q2 |
ε |
δ(q2, ε, a)={(q2, a)} |
a$ |
q2 |
| 6 |
q2 |
aabb |
δ(q2, b, $)={(q1, $)} |
$a |
q1 |
| 7 |
q1 |
ε |
δ(q1, ε, a)={(q2, ε)} |
$ |
q2 |
| 8 |
q2 |
aabb |
δ(q2, b, $)={(q1, $)} |
$ |
q1 |
| 9 |
q1 |
ε |
δ(q1, ε, $)={(q3, $)} |
$ |
q3 |
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...