Introduction to Power Analysis in Python
Last Updated :
26 Mar, 2021
To understand what power analysis is, we must first take a look at the concepts of a statistical hypothesis test. A statistical hypothesis test calculates some quantity under a given assumption (null hypothesis) and the result of the test allows us to interpret whether the assumption is valid or whether the assumption has been violated. A violation of the test’s assumption is often called the first hypothesis or alternative hypothesis. The p-value and critical values are the most common results of a statistical test which may be interpreted in different ways.
The p-value is compared to the significance level, 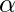 (specified before the experiment, and its value depends on the kind of experiment and business requirements). Typical significance level measures are 0.10 or 10%, 0.05 or 5%, and 0.01 or 1%.
(specified before the experiment, and its value depends on the kind of experiment and business requirements). Typical significance level measures are 0.10 or 10%, 0.05 or 5%, and 0.01 or 1%.
- If p-value <=
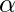 : Reject the null hypothesis (significant result).
: Reject the null hypothesis (significant result). - If p-value >
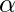 : Fail to reject the null hypothesis (not significant result).
: Fail to reject the null hypothesis (not significant result).
All statistical hypothesis tests have a chance of making either of the following types of errors:
- Type I Error: Incorrect rejection of a true null hypothesis or a false positive.
- Type II Error: Incorrect acceptance of a false null hypothesis or a false negative.
Statistical power: It is only relevant when the null hypothesis is false. The statistical power of a hypothesis test is the probability of correctly rejecting a null hypothesis or the likeliness of accepting the alternative hypothesis if it is true. So, the higher the statistical power for a given test, the lower the probability of making a Type II (false negative) error.
The last concept that you need to be aware of before proceeding to statistical power analysis is the effect size. It is the quantified magnitude of a result or effect present in a population of an experiment, usually measured by a specific statistical measure such as Pearson’s correlation or Cohen’s d for the difference in the means of two groups. The commonly accepted small, medium, large, and very large effect sizes for Cohen’s d are 0.20, 0.50, 0.80, and 1.3 respectively. The effect size or ‘expected effect’ is ascertained from pilot studies, findings from similar studies, field-defined effect, or an educated guess.
Power analysis: It is built from 4 variables, namely, Effect Size, Significance level, Power, Sample Size. All these variables are interrelated in the sense that changing one of them impacts the other three. Following this relationship, power analysis involves determining the fourth variable when the other three variables are known. It is a powerful tool for experimental design. For example, prior to an experiment, the sample size needed to detect a particular effect can be estimated given different desired levels of significance, effect size, and power. Alternatively, a study’s findings can be validated. Statistical power can be determined, by using the given sample size, effect size, and significance level, consequently helping to conclude whether the probability of committing a Type II error is acceptable from a decision-making perspective.
Power analysis using Python
The stats.power module of the statsmodels package in Python contains the required functions for carrying out power analysis for the most commonly used statistical tests such as t-test, normal based test, F-tests, and Chi-square goodness of fit test. It’s solve_power function takes 3 of the 4 variables mentioned above as input parameters and calculates the remaining 4th variable.
Consider a Student’s t-test, which is a statistical hypothesis test for comparing the means from two samples of Gaussian variables. In a pilot study with the two groups of variables, N1 = 4, Mean1 = 90, SD1 = 5; N2 = 4, Mean2 = 85, SD2 = 5. The assumption, or null hypothesis, of the test, is that the sample populations have the same mean. Since alpha is usually set to 0.05 and power to 0.80, the researcher primarily needs to be concerned with the sample size and the effect size. Let’s determine the sample size needed for the test in which a power of 80% is acceptable, with the significance level at 5% and the expected effect size to be found using the pilot study.
Example 1:
First, import the relevant libraries. Calculate the effect size using Cohen’s d. The TTestIndPower function implements Statistical Power calculations for t-test for two independent samples. Similarly, there are functions for F-test, Z-test and Chi-squared test. Next, initialize the variables for power analysis. Then using the solve_power function, we can get the required missing variable, which is the sample size in this case.
Code:
Python
from math import sqrt
from statsmodels.stats.power import TTestIndPower
n1, n2 = 4, 4
s1, s2 = 5**2, 5**2
s = sqrt(((n1 - 1) * s1 + (n2 - 1) * s2) / (n1 + n2 - 2))
u1, u2 = 90, 85
d = (u1 - u2) / s
print(f'Effect size: {d}')
alpha = 0.05
power = 0.8
obj = TTestIndPower()
n = obj.solve_power(effect_size=d, alpha=alpha, power=power,
ratio=1, alternative='two-sided')
print('Sample size/Number needed in each group: {:.3f}'.format(n))
|
Output:
Effect size: 1.0
Sample size/Number needed in each group: 16.715
So, the suggested minimum number of samples in each group required is 17 to have a significant p-value in the t-test. If we proceed and use an inferential t‐test before the power analysis, we may find a non‐significant p‐value even though there is a large effect, likely due to the small sample size (4).
Example 2:
Alternatively, we can test the power of a specific proposed sample size.
Code:
Python
from statsmodels.stats.power import TTestPower
power = TTestPower()
n_test = power.solve_power(nobs=40, effect_size = 0.5,
power = None, alpha = 0.05)
print('Power: {:.3f}'.format(n_test))
|
Output:
Power: 0.869
This tells us that a minimum sample size of 40 would result in a power of 0.87.
Example 3:
We can also plot power curves. Power curves are line plots that show how the change in effect size and sample size impact the power of the statistical test. The plot_power() function can be used to create power curves. ‘dep_var‘ argument specifies the dependent variable (x-axis) and can be ‘nobs’, ‘effect_size’ or ‘alpha’. Here, ‘nobs’ is the sample size and takes in array values. Due to this, one curve is created for each value of effect size.
Let’s assume a significance level of 0.05 and explore the change in sample size between 5 and 100 with Cohen’s d standard low, medium, and high effect sizes.
Code:
Python
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.stats.power import TTestIndPower
effect_sizes = np.array([0.2, 0.5, 0.8,1.3])
sample_sizes = np.array(range(5, 100))
obj = TTestIndPower()
obj.plot_power(dep_var='nobs', nobs=sample_sizes,
effect_size=effect_sizes)
plt.show()
|
Output:

Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...