Introduction to Mojette transform
Last Updated :
04 Sep, 2018
Data can be roughly divided into two types which are discrete data and continuous data. Discrete data can only take integer values where continuous data can take any value. The study of geometrical objects and properties of data which is discrete is called discrete geometry Discrete geometry has various application,its major application is of course the digital camera and screens.
The Mojette transform also use the discrete geometry fundamentals. To completely understand the Mojette transform we must understand Radon transform, Radon transform was developed by johann radon in 1917. Radon transform is a type of integral transform, the inverse of radon transform is used for reconstruction of images.Various applications of Radon transform are (as given in Stanley1993) in the field of Medicine , optics , astronomy, stress analysis, nuclear magnetic.
The Mojette Transform –
The mojette transform is a discrete and exact form of radon transform, Mojette is derived from a french word which means beans. The mojette transform uses a discrete geometry to store information onto a discrete geometrical support. This support is then projected by mojette transform in discrete directions. When it projects enough projections then reconstruction is possible.
The Mojette transform has 2 characteristics:
- Mojette transform can only use subtractions or additions for the reconstruction of the image.
- The transform uses discrete geometry.
The Mojette transform can be mathematically explained using the following equation:
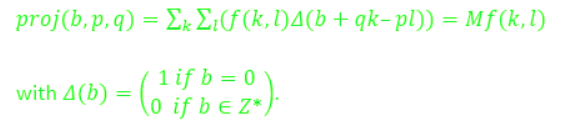
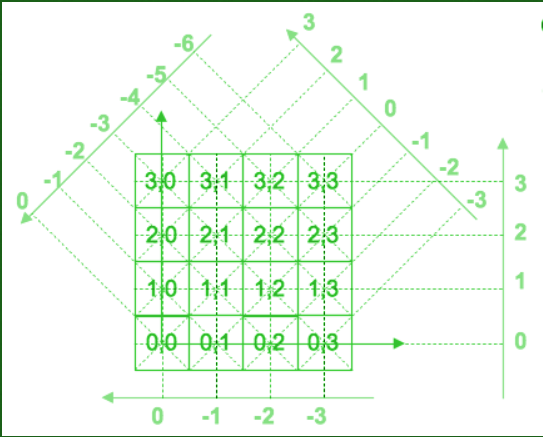
Figure below is an example of various direction in mojette transform in a 4*4 grid with 16 pixels:
Ghosts in discrete tomography –
The Mojette transform has many applications and mostly it gives unique result, but in some cases a unique result is not possible. In such cases we uses ghosts or phantoms to get all the possible reconstructions of the images that we can get from the Mojette transform. An example is shown in the figure where we can use ghost to get all the possible reconstructions when the result of Mojette transform is not unique:
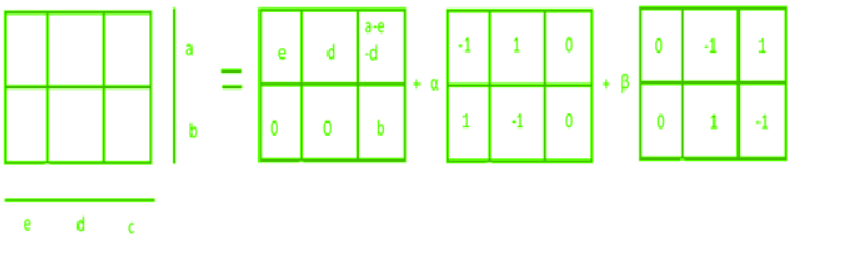
In simple language ghosts can be defined as object or noise added into the image but cannot be seen in the projections of the Mojette transform.
Application of ghosts –
- Error correcting code
- Distributed storage
- Network protocol
- Watermarking
- Medical Tomography
- Image Cryptography
- Image Fingerprinting
- Storage Distribution on networks or disks
Examples for phantoms –
- As seen in the figure below when we introduce a ghost in direction (1,1) that is when p=1 and q=1. The bin corresponding to the phantom shows no change.

- Similarly In the figure below, when a ghost is introduced in direction (0,1) that is when p=0 and q=1. The bin corresponding to the phantom shows no change.

- The above two examples are for the single projection, Figure 6 demonstrates an example of a multi projection ghost. In this figure, we have the ghost when the projections are (0,1),(1,1) and (-1,1).

Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...