Introduction to Min-Heap – Data Structure and Algorithm Tutorials

A Min-Heap is defined as a type of Heap Data Structure in which each internal node is smaller than or equal to its children. 

The heap data structure is a type of binary tree that is commonly used in computer science for various purposes, including sorting, searching, and organizing data.

Introduction to Min-Heap – Data Structure and Algorithm Tutorials

Purpose and Use Cases of Min-Heap:

• Priority Queue: One of the primary uses of the heap data structure is for implementing priority queues. 
• Dijkstra’s Algorithm: Dijkstra’s algorithm is a shortest path algorithm that finds the shortest path between two nodes in a graph. A min heap can be used to keep track of the unvisited nodes with the smallest distance from the source node.
• Sorting: A min heap can be used as a sorting algorithm to efficiently sort a collection of elements in ascending order.
• Median finding: A min heap can be used to efficiently find the median of a stream of numbers. We can use one min heap to store the larger half of the numbers and one max heap to store the smaller half. The median will be the root of the min heap.

Min-Heap Data structure in Different languages:

1. Min-Heap in C++

A min heap can be implemented using the priority_queue container from the Standard Template Library (STL). The priority_queue container is a type of container adapter that provides a way to store elements in a queue-like data structure in which each element has a priority associated with it.

Syntax: priority_queue < int, vector<int>, greater<int> > minH;

2. Min-Heap in Java

In Java, a min heap can be implemented using the PriorityQueue class from java.util package. The PriorityQueue class is a priority queue that provides a way to store elements in a queue-like data structure in which each element has a priority associated with it.

Syntax: PriorityQueue<Integer> minHeap = new PriorityQueue<Integer>(); 

3. Min-Heap in Python 

In Python, a min heap can be implemented using the heapq module, which provides functions for implementing heaps. Specifically, the heapq module provides a way to create and manipulate heap data structures.

Syntax: heap = []
        heapify(heap)

4. Min-Heap in C#

In C#, a min heap can be implemented using the PriorityQueue<T> class from the System.Collections.Generic namespace. The PriorityQueue<T> class is a priority queue that provides a way to store elements in a queue-like data structure in which each element has a priority associated with it.

Syntax: var minHeap = new PriorityQueue<int>();

5. Min-heap in JavaScript

A min heap is a binary tree where every node has a value less than or equal to its children. In JavaScript, you can implement a min heap using an array, where the first element represents the root node, and the children of a node at index i are located at indices 2i+1 and 2i+2.

Syntax: const minHeap = new MinHeap();

Difference between Max Heap and Min Heap

	Min Heap	Max Heap
1.	In a Min-Heap the key present at the root node must be less than or equal to among the keys present at all of its children.	In a Max-Heap the key present at the root node must be greater than or equal to among the keys present at all of its children.
2.	In a Min-Heap the minimum key element is present at the root.	In a Max-Heap the maximum key element is present at the root.
3.	A Min-Heap uses the ascending priority.	A Max-Heap uses the descending priority.
4.	In the construction of a Min-Heap, the smallest element has priority.	In the construction of a Max-Heap, the largest element has priority.
5.	In a Min-Heap, the smallest element is the first to be popped from the heap.	In a Max-Heap, the largest element is the first to be popped from the heap.

Internal Implementation of Min-Heap Data Structure:

A Min heap is typically represented as an array. 

• The root element will be at Arr[0]. 
• For any ith node Arr[i]:
  • Arr[(i -1) / 2] returns its parent node.
  • Arr[(2 * i) + 1] returns its left child node.
  • Arr[(2 * i) + 2] returns its right child node.

The Internal Implementation of the Min-Heap requires 3 major steps:

1. Insertion: To insert an element into the min heap, we first append the element to the end of the array and then adjust the heap property by repeatedly swapping the element with its parent until it is in the correct position.
2. Deletion: To remove the minimum element from the min heap, we first swap the root node with the last element in the array, remove the last element, and then adjust the heap property by repeatedly swapping the element with its smallest child until it is in the correct position.
3. Heapify: A heapify operation can be used to create a min heap from an unsorted array.

Operations on Min-heap Data Structure and their Implementation:

Here are some common operations that can be performed on a Heap Data Structure,

1. Insertion in Min-Heap Data Structure: 

Elements can be inserted into the heap following a similar approach as discussed above for deletion. The idea is to: 

• The insertion operation in a min-heap involves the following steps:
• Add the new element to the end of the heap, in the next available position in the last level of the tree.
• Compare the new element with its parent. If the parent is greater than the new element, swap them.
• Repeat step 2 until the parent is smaller than or equal to the new element, or until the new element reaches the root of the tree.
• The new element is now in its correct position in the min heap, and the heap property is satisfied.

Illustration:

Suppose the Heap is a Min-Heap as:

Insertion in Min-Heap

Implementation of insertion operation in Min-Heap:

C++

#include <iostream>
#include <vector>

using namespace std;

// Function to insert a new element into the min-heap
void insert_min_heap(vector<int>& heap, int value)
{
    // Add the new element to the end of the heap
    heap.push_back(value);
    // Get the index of the last element
    int index = heap.size() - 1;
    // Compare the new element with its parent and swap if
    // necessary
    while (index > 0
           && heap[(index - 1) / 2] > heap[index]) {
        swap(heap[index], heap[(index - 1) / 2]);
        // Move up the tree to the parent of the current
        // element
        index = (index - 1) / 2;
    }
}

// Main function to test the insert_min_heap function
int main()
{
    vector<int> heap;
    int values[] = { 10, 7, 11, 5, 4, 13 };
    int n = sizeof(values) / sizeof(values[0]);
    for (int i = 0; i < n; i++) {
        insert_min_heap(heap, values[i]);
        cout << "Inserted " << values[i]
             << " into the min-heap: ";
        for (int j = 0; j < heap.size(); j++) {
            cout << heap[j] << " ";
        }
        cout << endl;
    }
    return 0;
}

Java

import java.util.*;

public class GFG {

    // Function to insert a new element into the min-heap
    public static void insertMinHeap(int[] heap, int size,
                                     int value)
    {
        // Add the new element to the end of the heap
        heap[size] = value;
        // Get the index of the last element
        int index = size;
        // Compare the new element with its parent and swap
        // if necessary
        while (index > 0
               && heap[(index - 1) / 2] > heap[index]) {
            swap(heap, index, (index - 1) / 2);
            // Move up the tree to the parent of the current
            // element
            index = (index - 1) / 2;
        }
    }

    // Function to swap two elements in an array
    public static void swap(int[] arr, int i, int j)
    {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

    // Main function to test the insertMinHeap function
    public static void main(String[] args)
    {
        int[] heap = new int[6];
        int[] values = { 10, 7, 11, 5, 4, 13 };
        int size = 0;
        for (int i = 0; i < values.length; i++) {
            insertMinHeap(heap, size, values[i]);
            size++;
            System.out.print("Inserted " + values[i]
                             + " into the min-heap: ");
            for (int j = 0; j < size; j++) {
                System.out.print(heap[j] + " ");
            }
            System.out.println();
        }
    }
}

C#

using System;
using System.Collections.Generic;

public class Program {
    // Function to insert a new element into the min-heap
    static void InsertMinHeap(List<int> heap, int value)
    {
        // Add the new element to the end of the heap
        heap.Add(value);
        // Get the index of the last element
        int index = heap.Count - 1;
        // Compare the new element with its parent and swap
        // if necessary
        while (index > 0
               && heap[(index - 1) / 2] > heap[index]) {
            int temp = heap[index];
            heap[index] = heap[(index - 1) / 2];
            heap[(index - 1) / 2] = temp;
            // Move up the tree to the parent of the current
            // element
            index = (index - 1) / 2;
        }
    }

    // Main function to test the InsertMinHeap function
    public static void Main()
    {
        List<int> heap = new List<int>();
        int[] values = { 10, 7, 11, 5, 4, 13 };
        foreach(int value in values)
        {
            InsertMinHeap(heap, value);
            Console.Write("Inserted " + value
                          + " into the min-heap: ");
            foreach(int element in heap)
            {
                Console.Write(element + " ");
            }
            Console.WriteLine();
        }
    }
}

Javascript

function insertMinHeap(heap, value) {
  heap.push(value);
  let index = heap.length - 1;
  let parentIndex = Math.floor((index - 1) / 2);
  while (index > 0 && heap[parentIndex] > heap[index]) {
    [heap[index], heap[parentIndex]] = [heap[parentIndex], heap[index]];
    index = parentIndex;
    parentIndex = Math.floor((index - 1) / 2);
  }
}

// Example usage
const heap = [];
const values = [10, 7, 11, 5, 4, 13];
for (const value of values) {
  insertMinHeap(heap, value);
  console.log(`Inserted ${value} into the min-heap: ${heap}`);
}

Python3

def insert_min_heap(heap, value):
    # Add the new element to the end of the heap
    heap.append(value)
    # Get the index of the last element
    index = len(heap) - 1
    # Compare the new element with its parent and swap if necessary
    while index > 0 and heap[(index - 1) // 2] > heap[index]:
        heap[index], heap[(index - 1) //
                          2] = heap[(index - 1) // 2], heap[index]
        # Move up the tree to the parent of the current element
        index = (index - 1) // 2


heap = []
values = [10, 7, 11, 5, 4, 13]
for value in values:
    insert_min_heap(heap, value)
    print(f"Inserted {value} into the min-heap: {heap}")

Output

Inserted 10 into the min-heap: 10 
Inserted 7 into the min-heap: 7 10 
Inserted 11 into the min-heap: 7 10 11 
Inserted 5 into the min-heap: 5 7 11 10 
Inserted 4 into the min-heap: 4 5 11 10 7 
Inser...

Time Complexity:  O(log(n)) (where n is no of elements in the heap)
Auxiliary Space: O(n)

2. Deletion in Min-Heap Data Structure:

Removing the smallest element (the root) from the min heap. The root is replaced by the last element in the heap, and then the heap property is restored by swapping the new root with its smallest child until the parent is smaller than both children or until the new root reaches a leaf node.

• Replace the root or element to be deleted with the last element.
• Delete the last element from the Heap.
• Since the last element is now placed at the position of the root node. So, it may not follow the heap property. Therefore, heapify the last node placed at the position of the root.

Illustration:  

Suppose the Heap is a Min-Heap as:

Min-Heap Data Structure

The element to be deleted is root, i.e. 13.

Process:

The last element is 100.

Step 1: Replace the last element with root, and delete it.

Min-Heap Data Structure

Step 2: Heapify root.

Final Heap:

Min-Heap Data Structure

Implementation of Deletion operation in Min-Heap:

C++

#include <iostream>
#include <vector>

using namespace std;

// Function to insert a new element into the min-heap
void insert_min_heap(vector<int>& heap, int value)
{
    // Add the new element to the end of the heap
    heap.push_back(value);
    // Get the index of the last element
    int index = heap.size() - 1;
    // Compare the new element with its parent and swap if
    // necessary
    while (index > 0
           && heap[(index - 1) / 2] > heap[index]) {
        swap(heap[index], heap[(index - 1) / 2]);
        // Move up the tree to the parent of the current
        // element
        index = (index - 1) / 2;
    }
}

// Function to delete a node from the min-heap
void delete_min_heap(vector<int>& heap, int value)
{
    // Find the index of the element to be deleted
    int index = -1;
    for (int i = 0; i < heap.size(); i++) {
        if (heap[i] == value) {
            index = i;
            break;
        }
    }
    // If the element is not found, return
    if (index == -1) {
        return;
    }
    // Replace the element to be deleted with the last
    // element
    heap[index] = heap[heap.size() - 1];
    // Remove the last element
    heap.pop_back();
    // Heapify the tree starting from the element at the
    // deleted index
    while (true) {
        int left_child = 2 * index + 1;
        int right_child = 2 * index + 2;
        int smallest = index;
        if (left_child < heap.size()
            && heap[left_child] < heap[smallest]) {
            smallest = left_child;
        }
        if (right_child < heap.size()
            && heap[right_child] < heap[smallest]) {
            smallest = right_child;
        }
        if (smallest != index) {
            swap(heap[index], heap[smallest]);
            index = smallest;
        }
        else {
            break;
        }
    }
}

// Main function to test the insert_min_heap and
// delete_min_heap functions
int main()
{
    vector<int> heap;
    int values[] = { 13, 16, 31, 41, 51, 100 };
    int n = sizeof(values) / sizeof(values[0]);
    for (int i = 0; i < n; i++) {
        insert_min_heap(heap, values[i]);
    }
    cout << "Initial heap: ";
    for (int j = 0; j < heap.size(); j++) {
        cout << heap[j] << " ";
    }
    cout << endl;

    delete_min_heap(heap, 13);
    cout << "Heap after deleting 13: ";
    for (int j = 0; j < heap.size(); j++) {
        cout << heap[j] << " ";
    }
    cout << endl;

    return 0;
}

Java

import java.util.*;

public class GFG {
    // Function to insert a new element into the min-heap
    public static void insertMinHeap(List<Integer> heap,
                                     int value)
    {
        // Add the new element to the end of the heap
        heap.add(value);
        // Get the index of the last element
        int index = heap.size() - 1;
        // Compare the new element with its parent and swap
        // if necessary
        while (index > 0
               && heap.get((index - 1) / 2)
                      > heap.get(index)) {
            Collections.swap(heap, index, (index - 1) / 2);
            // Move up the tree to the parent of the current
            // element
            index = (index - 1) / 2;
        }
    }

    // Function to delete a node from the min-heap
    public static void deleteMinHeap(List<Integer> heap,
                                     int value)
    {
        // Find the index of the element to be deleted
        int index = -1;
        for (int i = 0; i < heap.size(); i++) {
            if (heap.get(i) == value) {
                index = i;
                break;
            }
        }
        // If the element is not found, return
        if (index == -1) {
            return;
        }
        // Replace the element to be deleted with the last
        // element
        heap.set(index, heap.get(heap.size() - 1));
        // Remove the last element
        heap.remove(heap.size() - 1);
        // Heapify the tree starting from the element at the
        // deleted index
        while (true) {
            int leftChild = 2 * index + 1;
            int rightChild = 2 * index + 2;
            int smallest = index;
            if (leftChild < heap.size()
                && heap.get(leftChild)
                       < heap.get(smallest)) {
                smallest = leftChild;
            }
            if (rightChild < heap.size()
                && heap.get(rightChild)
                       < heap.get(smallest)) {
                smallest = rightChild;
            }
            if (smallest != index) {
                Collections.swap(heap, index, smallest);
                index = smallest;
            }
            else {
                break;
            }
        }
    }

    // Main function to test the insertMinHeap and
    // deleteMinHeap functions
    public static void main(String[] args)
    {
        List<Integer> heap = new ArrayList<Integer>();
        int[] values = { 13, 16, 31, 41, 51, 100 };
        int n = values.length;
        for (int i = 0; i < n; i++) {
            insertMinHeap(heap, values[i]);
        }
        System.out.print("Initial heap: ");
        for (int j = 0; j < heap.size(); j++) {
            System.out.print(heap.get(j) + " ");
        }
        System.out.println();

        deleteMinHeap(heap, 13);
        System.out.print("Heap after deleting 13: ");
        for (int j = 0; j < heap.size(); j++) {
            System.out.print(heap.get(j) + " ");
        }
        System.out.println();
    }
}

C#

using System;
using System.Collections.Generic;

class MinHeap {
    private List<int> heap = new List<int>();

    public void Insert(int value)
    {
        heap.Add(value);
        int index = heap.Count - 1;
        while (index > 0
               && heap[(index - 1) / 2] > heap[index]) {
            Swap(index, (index - 1) / 2);
            index = (index - 1) / 2;
        }
    }

    public void Delete(int value)
    {
        int index = heap.IndexOf(value);
        if (index == -1) {
            return;
        }
        heap[index] = heap[heap.Count - 1];
        heap.RemoveAt(heap.Count - 1);
        while (true) {
            int leftChild = 2 * index + 1;
            int rightChild = 2 * index + 2;
            int smallest = index;
            if (leftChild < heap.Count
                && heap[leftChild] < heap[smallest]) {
                smallest = leftChild;
            }
            if (rightChild < heap.Count
                && heap[rightChild] < heap[smallest]) {
                smallest = rightChild;
            }
            if (smallest != index) {
                Swap(index, smallest);
                index = smallest;
            }
            else {
                break;
            }
        }
    }

    private void Swap(int i, int j)
    {
        int temp = heap[i];
        heap[i] = heap[j];
        heap[j] = temp;
    }

    public void Print()
    {
        for (int i = 0; i < heap.Count; i++) {
            Console.Write(heap[i] + " ");
        }
        Console.WriteLine();
    }
}

class Program {
    static void Main(string[] args)
    {
        MinHeap heap = new MinHeap();
        int[] values = { 13, 16, 31, 41, 51, 100 };
        for (int i = 0; i < values.Length; i++) {
            heap.Insert(values[i]);
        }
        Console.Write("Initial heap: ");
        heap.Print();

        heap.Delete(13);
        Console.Write("Heap after deleting 13: ");
        heap.Print();
    }
}

Javascript

function insertMinHeap(heap, value) {
  // Add the new element to the end of the heap
  heap.push(value);
  // Get the index of the last element
  let index = heap.length - 1;
  // Compare the new element with its parent and swap if necessary
  for (let flr = Math.floor((index - 1) / 2); index > 0 && heap[flr] > heap[index]; flr = Math.floor((index - 1) / 2)) {
    [heap[index], heap[flr]] = [
      heap[flr],
      heap[index],
    ];
    // Move up the tree to the parent of the current element
    index = Math.floor((index - 1) / 2);
  }
}

function deleteMinHeap(heap, value) {
  // Find the index of the element to be deleted
  let index = -1;
  for (let i = 0; i < heap.length; i++) {
    if (heap[i] == value) {
      index = i;
      break;
    }
  }
  // If the element is not found, return
  if (index == -1) {
    return;
  }
  // Replace the element to be deleted with the last element
  heap[index] = heap[heap.length - 1];
  // Remove the last element
  heap.pop();
  // Heapify the tree starting from the element at the deleted index
  while (true) {
    let left_child = 2 * index + 1;
    let right_child = 2 * index + 2;
    let smallest = index;
    if (left_child < heap.length && heap[left_child] < heap[smallest]) {
      smallest = left_child;
    }
    if (right_child < heap.length && heap[right_child] < heap[smallest]) {
      smallest = right_child;
    }
    if (smallest != index) {
      [heap[index], heap[smallest]] = [heap[smallest], heap[index]];
      index = smallest;
    } else {
      break;
    }
  }
}

// Main function to test the insertMinHeap and deleteMinHeap functions
let heap = [];
let values = [13, 16, 31, 41, 51, 100];
for (let i = 0; i < values.length; i++) {
  insertMinHeap(heap, values[i]);
}
console.log("Initial heap: " + heap.join(" "));

deleteMinHeap(heap, 13);
console.log("Heap after deleting 13: " + heap.join(" "));

Python3

def insert_min_heap(heap, value):
    heap.append(value)
    index = len(heap) - 1
    while index > 0 and heap[(index - 1) // 2] > heap[index]:
        heap[index], heap[(index - 1) //
                          2] = heap[(index - 1) // 2], heap[index]
        index = (index - 1) // 2


def delete_min_heap(heap, value):
    index = -1
    for i in range(len(heap)):
        if heap[i] == value:
            index = i
            break
    if index == -1:
        return
    heap[index] = heap[-1]
    heap.pop()
    while True:
        left_child = 2 * index + 1
        right_child = 2 * index + 2
        smallest = index
        if left_child < len(heap) and heap[left_child] < heap[smallest]:
            smallest = left_child
        if right_child < len(heap) and heap[right_child] < heap[smallest]:
            smallest = right_child
        if smallest != index:
            heap[index], heap[smallest] = heap[smallest], heap[index]
            index = smallest
        else:
            break


heap = []
values = [13, 16, 31, 41, 51, 100]
for value in values:
    insert_min_heap(heap, value)
print("Initial heap:", heap)

delete_min_heap(heap, 13)
print("Heap after deleting 13:", heap)

Output

Initial heap: 13 16 31 41 51 100 
Heap after deleting 13: 16 41 31 100 51 

Time complexity: O(log n) where n is no of elements in the heap
Auxiliary Space: O(n)

3. Peek operation on Min-Heap Data Structure:

 To access the minimum element (i.e., the root of the heap), the value of the root node is returned. The time complexity of peek in a min-heap is O(1).

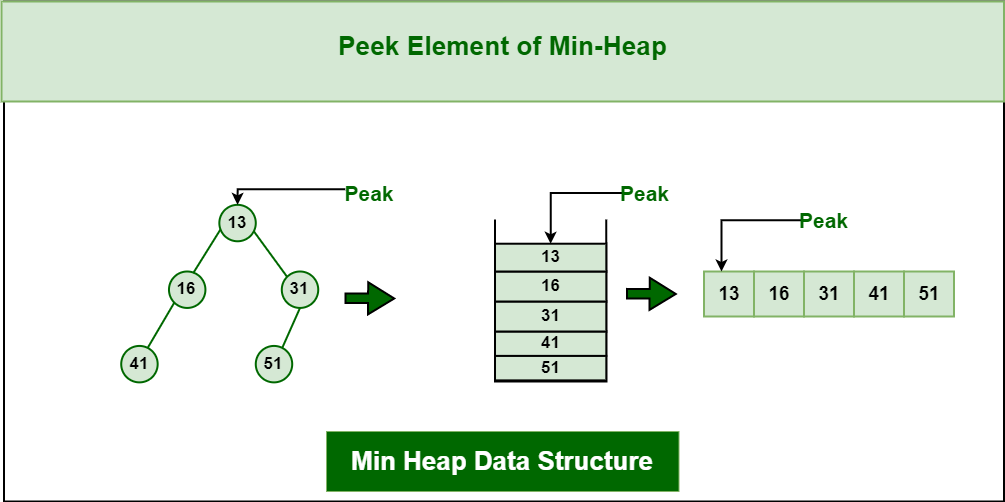
Min Heap Data Structure

Implementation of Peek operation in Min-Heap:

C++

#include <iostream>
#include <queue>
#include <vector>
using namespace std;

int main()
{
    // Create a max heap with some elements using a
    // priority_queue
    priority_queue<int, vector<int>, greater<int> > minHeap;
    minHeap.push(9);
    minHeap.push(8);
    minHeap.push(7);
    minHeap.push(6);
    minHeap.push(5);
    minHeap.push(4);
    minHeap.push(3);
    minHeap.push(2);
    minHeap.push(1);

    // Get the peak element (i.e., the largest element)
    int peakElement = minHeap.top();

    // Print the peak element
    cout << "Peak element: " << peakElement << std::endl;

    return 0;
}

Java

import java.util.PriorityQueue;

public class GFG {
    public static void main(String[] args)
    {
        // Create a max heap with some elements using a
        // PriorityQueue
        PriorityQueue<Integer> minHeap
            = new PriorityQueue<>();
        minHeap.add(9);
        minHeap.add(8);
        minHeap.add(7);
        minHeap.add(6);
        minHeap.add(5);
        minHeap.add(4);
        minHeap.add(3);
        minHeap.add(2);
        minHeap.add(1);

        // Get the peak element (i.e., the largest element)
        int peakElement = minHeap.peek();

        // Print the peak element
        System.out.println("Peak element: " + peakElement);
    }
}

C#

using System;
using System.Collections.Generic;

public class GFG {
    public static void Main()
    {
        // Create a min heap with some elements using a
        // PriorityQueue
        var minHeap = new PriorityQueue<int>();
        minHeap.Enqueue(9);
        minHeap.Enqueue(8);
        minHeap.Enqueue(7);
        minHeap.Enqueue(6);
        minHeap.Enqueue(5);
        minHeap.Enqueue(4);
        minHeap.Enqueue(3);
        minHeap.Enqueue(2);
        minHeap.Enqueue(1);

        // Get the peak element (i.e., the smallest element)
        int peakElement = minHeap.Peek();

        // Print the peak element
        Console.WriteLine("Peak element: " + peakElement);
    }
}

Javascript

const PriorityQueue = require('fast-priority-queue');

// Create a min heap with some elements using a PriorityQueue
const minHeap = new PriorityQueue((a, b) => a - b);
minHeap.add(9);
minHeap.add(8);
minHeap.add(7);
minHeap.add(6);
minHeap.add(5);
minHeap.add(4);
minHeap.add(3);
minHeap.add(2);
minHeap.add(1);

// Get the peak element (i.e., the smallest element)
const peakElement = minHeap.peek();

// Print the peak element
console.log(`Peak element: ${peakElement}`);

Python3

import heapq

# Create a min heap with some elements using a list
min_heap = [9, 8, 7, 6, 5, 4, 3, 2, 1]
heapq.heapify(min_heap)

# Get the peak element (i.e., the smallest element)
peak_element = heapq.nsmallest(1, min_heap)[0]

# Print the peak element
print("Peak element:", peak_element)

Output

Peak element: 1

Time complexity: In a min heap implemented using an array or a list, the peak element can be accessed in constant time, O(1), as it is always located at the root of the heap.
In a min heap implemented using a binary tree, the peak element can also be accessed in O(1) time, as it is always located at the root of the tree.

Auxiliary Space: O(n)

4. Heapify operation on Min-Heap Data Structure:

A heapify operation can be used to create a min heap from an unsorted array. This is done by starting at the last non-leaf node and repeatedly performing the “bubble down” operation until all nodes satisfy the heap property. 

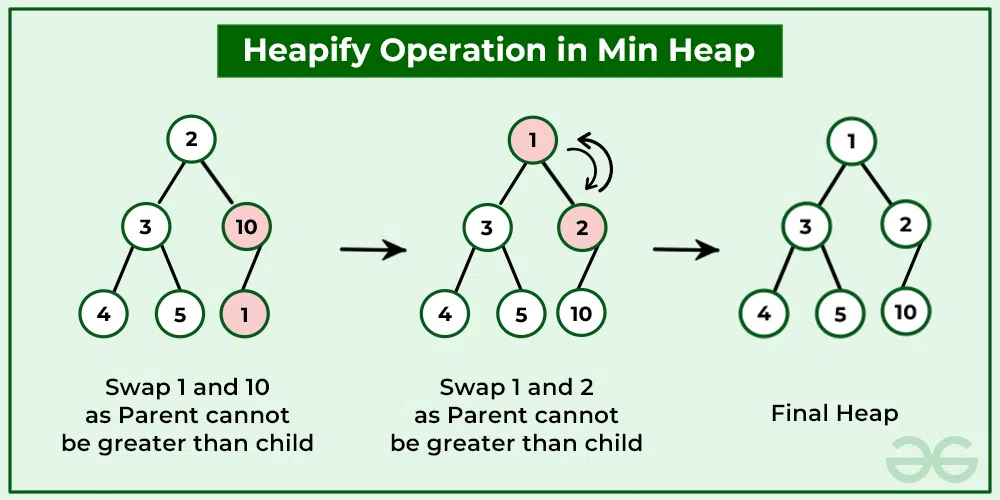
Heapify operation in Min Heap

Implementation of Heapify  operation in Min-Heap:

C++

#include <iostream>
#include <vector>
using namespace std;

void minHeapify(vector<int> &arr, int i, int n) {
    int smallest = i;
    int l = 2*i + 1;
    int r = 2*i + 2;

    if (l < n && arr[l] < arr[smallest])
        smallest = l;

    if (r < n && arr[r] < arr[smallest])
        smallest = r;

    if (smallest != i) {
        swap(arr[i], arr[smallest]);
        minHeapify(arr, smallest, n);
    }
}

int main() {
    vector<int> arr = {10, 5, 15, 2, 20, 30};

    cout << "Original array: ";
    for (int i = 0; i < arr.size(); i++)
        cout << arr[i] << " ";

    // Perform heapify operation on min-heap
    for (int i = arr.size()/2 - 1; i >= 0; i--)
        minHeapify(arr, i, arr.size());

    cout << "\nMin-Heap after heapify operation: ";
    for (int i = 0; i < arr.size(); i++)
        cout << arr[i] << " ";

    return 0;
}

Java

// Java code of Heapify operation in Min-Heap

import java.util.Arrays;
import java.util.List;

public class Main {
    // Function to maintain the min-heap property of the heap rooted at index 'i'
    public static void minHeapify(List<Integer> arr, int i, int n) {
        // Assume the root is the smallest element initially
        int smallest = i;
        // Calculate the indices of the left and right child of the current node
        int l = 2 * i + 1;
        int r = 2 * i + 2;

        // Compare the left child with the current smallest
        if (l < n && arr.get(l) < arr.get(smallest))
            smallest = l;

        // Compare the right child with the current smallest
        if (r < n && arr.get(r) < arr.get(smallest))
            smallest = r;

        // If the current node is not the smallest, swap it with the smallest child
        if (smallest != i) {
            int temp = arr.get(i);
            arr.set(i, arr.get(smallest));
            arr.set(smallest, temp);
            // Recursively heapify the subtree rooted at the smallest child
            minHeapify(arr, smallest, n);
        }
    }

    public static void main(String[] args) {
        // Create a list representing the array
        List<Integer> arr = Arrays.asList(10, 5, 15, 2, 20, 30);

        System.out.print("Original array: ");
        // Print the original array
        for (int i = 0; i < arr.size(); i++)
            System.out.print(arr.get(i) + " ");

        // Perform heapify operation on the min-heap
        // Start from the last non-leaf node and go up to the root of the tree
        for (int i = arr.size() / 2 - 1; i >= 0; i--)
            minHeapify(arr, i, arr.size());

        System.out.print("\nMin-Heap after heapify operation: ");
        // Print the min-heap after heapify operation
        for (int i = 0; i < arr.size(); i++)
            System.out.print(arr.get(i) + " ");
    }
}

Python

def minHeapify(arr, i, n):
    smallest = i
    left = 2 * i + 1
    right = 2 * i + 2

    if left < n and arr[left] < arr[smallest]:
        smallest = left

    if right < n and arr[right] < arr[smallest]:
        smallest = right

    if smallest != i:
        arr[i], arr[smallest] = arr[smallest], arr[i]
        minHeapify(arr, smallest, n)

if __name__ == "__main__":
    arr = [10, 5, 15, 2, 20, 30]

    print("Original array:", arr)

    # Perform heapify operation on a min-heap
    for i in range(len(arr) // 2 - 1, -1, -1):
        minHeapify(arr, i, len(arr))

    print("Min-Heap after heapify operation:", arr)

C#

using System;
using System.Collections.Generic;

class GFG
{
    // Function to perform the minHeapify operation on a min-heap.
    static void MinHeapify(List<int> arr, int i, int n)
    {
        int smallest = i;
        int left = 2 * i + 1;
        int right = 2 * i + 2;
        // Compare the left child with the current smallest node.
        if (left < n && arr[left] < arr[smallest])
            smallest = left;
        // Compare the right child with the current smallest node.
        if (right < n && arr[right] < arr[smallest])
            smallest = right;
        // If the current node is not the smallest
        // swap it with the smallest child.
        if (smallest != i)
        {
            int temp = arr[i];
            arr[i] = arr[smallest];
            arr[smallest] = temp;
            // Recursively call minHeapify on the affected subtree.
            MinHeapify(arr, smallest, n);
        }
    }
    static void Main(string[] args)
    {
        List<int> arr = new List<int> { 10, 5, 15, 2, 20, 30 };
        Console.Write("Original array: ");
        foreach (int num in arr)
            Console.Write(num + " ");
        // Perform heapify operation on the min-heap.
        for (int i = arr.Count / 2 - 1; i >= 0; i--)
            MinHeapify(arr, i, arr.Count);
        Console.Write("\nMin-Heap after heapify operation: ");
        foreach (int num in arr)
            Console.Write(num + " ");
    }
}

Javascript

// Define a function to perform min-heapify operation on an array
function minHeapify(arr, i, n) {
    let smallest = i;
    let l = 2 * i + 1;
    let r = 2 * i + 2;

    // Check if left child is smaller than the current smallest element
    if (l < n && arr[l] < arr[smallest])
        smallest = l;

    // Check if right child is smaller than the current smallest element
    if (r < n && arr[r] < arr[smallest])
        smallest = r;

    // If the smallest element is not the current element, swap them
    if (smallest !== i) {
        [arr[i], arr[smallest]] = [arr[smallest], arr[i]];
        minHeapify(arr, smallest, n);
    }
}

// Main function
function main() {
    const arr = [10, 5, 15, 2, 20, 30];

    // Print the original array
    console.log("Original array: " + arr.join(" "));

    // Perform heapify operation on the min-heap
    for (let i = Math.floor(arr.length / 2) - 1; i >= 0; i--)
        minHeapify(arr, i, arr.length);

    // Print the min-heap after heapify operation
    console.log("Min-Heap after heapify operation: " + arr.join(" "));
}

// Call the main function to start the process
main();

Output

Original array: 10 5 15 2 20 30 
Min-Heap after heapify operation: 2 5 15 10 20 30 

The time complexity of heapify in a min-heap is O(n).

5. Search operation on Min-Heap Data Structure: 

To search for an element in the min heap, a linear search can be performed over the array that represents the heap. However, the time complexity of a linear search is O(n), which is not efficient. Therefore, searching is not a commonly used operation in a min heap.

Here’s an example code that shows how to search for an element in a min heap using std::find():

C++

#include <bits/stdc++.h>
using namespace std;

int main()
{
    priority_queue<int, vector<int>, greater<int> >
        min_heap;
    // example max heap

    min_heap.push(10);
    min_heap.push(9);
    min_heap.push(8);
    min_heap.push(6);
    min_heap.push(4);

    int element = 6; // element to search for
    bool found = false;

    // Copy the min heap to a temporary queue and search for
    // the element
    std::priority_queue<int, vector<int>, greater<int> >
        temp = min_heap;
    while (!temp.empty()) {
        if (temp.top() == element) {
            found = true;
            break;
        }
        temp.pop();
    }

    if (found) {
        std::cout << "Element found in the min heap."
                  << std::endl;
    }
    else {
        std::cout << "Element not found in the min heap."
                  << std::endl;
    }

    return 0;
}

Java

import java.util.PriorityQueue;

public class GFG {
    public static void main(String[] args)
    {
        PriorityQueue<Integer> min_heap
            = new PriorityQueue<>();
        min_heap.add(
            3); // insert elements into the priority queue
        min_heap.offer(1);
        min_heap.offer(4);
        min_heap.offer(1);
        min_heap.offer(6);

        int element = 6; // element to search for
        boolean found = false;

        // Copy the min heap to a temporary queue and search
        // for the element
        PriorityQueue<Integer> temp
            = new PriorityQueue<>(min_heap);
        while (!temp.isEmpty()) {
            if (temp.poll() == element) {
                found = true;
                break;
            }
        }

        if (found) {
            System.out.println(
                "Element found in the min heap.");
        }
        else {
            System.out.println(
                "Element not found in the min heap.");
        }
    }
}

C#

using System;
using System.Collections.Generic;

public class GFG {
    public static void Main()
    {
        var minHeap = new PriorityQueue<int>();
        // example min heap
        minHeap.Enqueue(4);
        minHeap.Enqueue(6);
        minHeap.Enqueue(8);
        minHeap.Enqueue(9);
        minHeap.Enqueue(10);

        int element = 6; // element to search for
        bool found = false;

        // Copy the min heap to a temporary queue and search
        // for the element
        var temp = new PriorityQueue<int>(minHeap);
        while (temp.Count > 0) {
            if (temp.Peek() == element) {
                found = true;
                break;
            }
            temp.Dequeue();
        }

        if (found) {
            Console.WriteLine(
                "Element found in the min heap.");
        }
        else {
            Console.WriteLine(
                "Element not found in the min heap.");
        }
    }
}

Javascript

// Example min heap
let minHeap = new PriorityQueue();
minHeap.enqueue(4);
minHeap.enqueue(6);
minHeap.enqueue(8);
minHeap.enqueue(9);
minHeap.enqueue(10);

let element = 6; // Element to search for
let found = false;

// Copy the min heap to a temporary queue and search for the element
let temp = new PriorityQueue(minHeap);
while (temp.size() > 0) {
    if (temp.peek() == element) {
        found = true;
        break;
    }
    temp.dequeue();
}

if (found) {
    console.log("Element found in the min heap.");
} else {
    console.log("Element not found in the min heap.");
}

Python3

import heapq

min_heap = [1, 2, 3, 5, 6, 7, 8, 10]  # example min heap
heapq.heapify(min_heap)

element = 6  # element to search for
found = False

# Copy the min heap to a temporary list and search for the element
temp = list(min_heap)
while temp:
    if heapq.heappop(temp) == element:
        found = True
        break

if found:
    print("Element found in the min heap.")
else:
    print("Element not found in the min heap.")

Output

Element found in the min heap.

 Complexity analysis: 

The time complexity of this program is O(n log n), where n is the number of elements in the priority queue.

The insertion operation has a time complexity of O(log n) in the worst case because the heap property needs to be maintained. The search operation involves copying the priority queue to a temporary queue and then traversing the temporary queue, which takes O(n log n) time in the worst case because each element needs to be copied and popped from the queue, and the priority queue needs to be rebuilt for each operation.

The space complexity of the program is O(n) because it stores n elements in the priority queue and creates a temporary queue with n elements.

Applications of Min-Heap Data Structure:

• Heap sort: Min heap is used as a key component in heap sort algorithm which is an efficient sorting algorithm with a time complexity of O(nlogn).
• Priority Queue: A priority queue can be implemented using a min heap data structure where the element with the minimum value is always at the root.
• Dijkstra’s algorithm: In Dijkstra’s algorithm, a min heap is used to store the vertices of the graph with the minimum distance from the starting vertex. The vertex with the minimum distance is always at the root of the heap.
• Huffman coding: In Huffman coding, a min heap is used to implement a priority queue to build an optimal prefix code for a given set of characters.
• Merge K sorted arrays: Given K sorted arrays, we can merge them into a single sorted array efficiently using a min heap data structure.

Advantages of Min-heap Data Structure:

• Efficient insertion and deletion: Min heap allows fast insertion and deletion of elements with a time complexity of O(log n), where n is the number of elements in the heap.
• Efficient retrieval of minimum element: The minimum element in a min heap is always at the root of the heap, which can be retrieved in O(1) time.
• Space efficient: Min heap is a compact data structure that can be implemented using an array or a binary tree, which makes it space efficient.
• Sorting: Min heap can be used to implement an efficient sorting algorithm such as heap sort with a time complexity of O(n log n).
• Priority Queue: Min heap can be used to implement a priority queue, where the element with the minimum priority can be retrieved efficiently in O(1) time.
• Versatility: Min heap has several applications in computer science, including graph algorithms, data compression, and database systems.

Overall, min heap is a useful and versatile data structure that offers efficient operations, space efficiency, and has several applications in computer science.