Introduction of Logic Gates
Last Updated :
06 Dec, 2023
In Boolean Algebra, there are three basic operations,  which are analogous to disjunction, conjunction, and negation in propositional logic. Each of these operations has a corresponding logic gate. Apart from these there are a few other logic gates as well. It was invented by George Boole.
which are analogous to disjunction, conjunction, and negation in propositional logic. Each of these operations has a corresponding logic gate. Apart from these there are a few other logic gates as well. It was invented by George Boole.
Gate- A gate can be defined as a digital circuit which can allow a signal(electric current) to pass or stop.
Logic Gate- A type of gate that allows a signal to pass through when certain logical conditions are met. Different logic gates have different logical conditions.
- AND Gate(.) – The AND gate gives an output of 1 when if both the two inputs are 1, it gives 0 otherwise. For n-input gate if all the inputs are 1 then 1 otherwise 0.
- OR Gate(+) – The OR gate gives an output of 1 if either of the two inputs are 1, it gives 0 otherwise. For n-input gate if all the inputs are 0 then 0 otherwise 1.
- NOT Gate(‘) – The NOT gate gives an output of 1 if the input is 0 and vice-versa.
- XOR Gate(
 ) – The XOR gate gives an output of 1 if either both inputs are different, it gives 0 if they are same. For n-input gate if the number of input 1 are odd then it gives 1 otherwise 0.
) – The XOR gate gives an output of 1 if either both inputs are different, it gives 0 if they are same. For n-input gate if the number of input 1 are odd then it gives 1 otherwise 0.
Truth Table- A truth table is a table that shows all possible combinations of inputs and outputs for a logic gate.
Four more logic gates are obtained if the output of above-mentioned gates is negated.
- NAND Gate(
 )- The NAND gate (negated AND) gives an output of 0 if both inputs are 1, it gives 1 otherwise. For n-input gate if all inputs are 1 then it gives 0 otherwise 1.
)- The NAND gate (negated AND) gives an output of 0 if both inputs are 1, it gives 1 otherwise. For n-input gate if all inputs are 1 then it gives 0 otherwise 1. - NOR Gate(
 )- The NOR gate (negated OR) gives an output of 1 only if both inputs are 0, it gives 0 otherwise. For n-input gate if all inputs are 0 then it gives 1 otherwise 0.
)- The NOR gate (negated OR) gives an output of 1 only if both inputs are 0, it gives 0 otherwise. For n-input gate if all inputs are 0 then it gives 1 otherwise 0. - XNOR Gate(
 )- The XNOR gate (negated XOR) gives an output of 1 if both inputs are same and 0 if they are different. For n-input gate if the number of input 1 are even then it gives 1 otherwise odd.
)- The XNOR gate (negated XOR) gives an output of 1 if both inputs are same and 0 if they are different. For n-input gate if the number of input 1 are even then it gives 1 otherwise odd. - BUFFER Gate( )- The BUFFER gate is the opposite of the NOT gate, as its output is 1 if its input is 1 and vice-versa.
Every Logic gate has a graphical representation or symbol associated with it. Below is an image which shows the graphical symbols and truth tables associated with each logic gate. 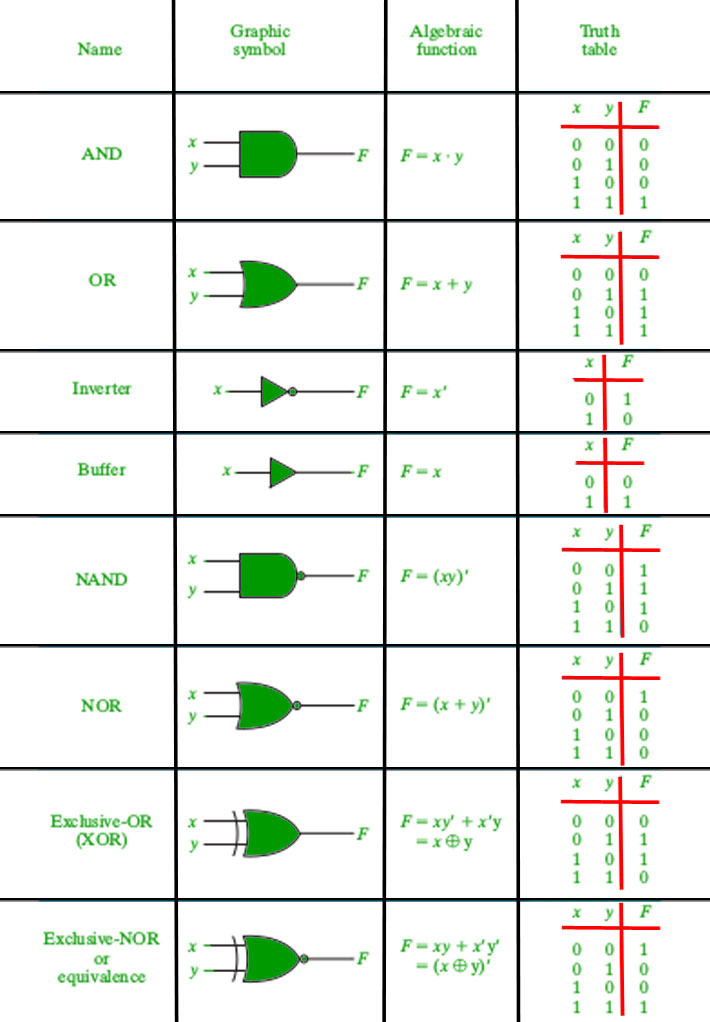
Universal Logic Gates – Out of the eight logic gates discussed above, NAND and NOR are also known as universal gates since they can be used to implement any digital circuit without using any other gate. This means that every gate can be created by NAND or NOR gates only. Implementation of three basic gates using NAND and NOR gates is shown below – 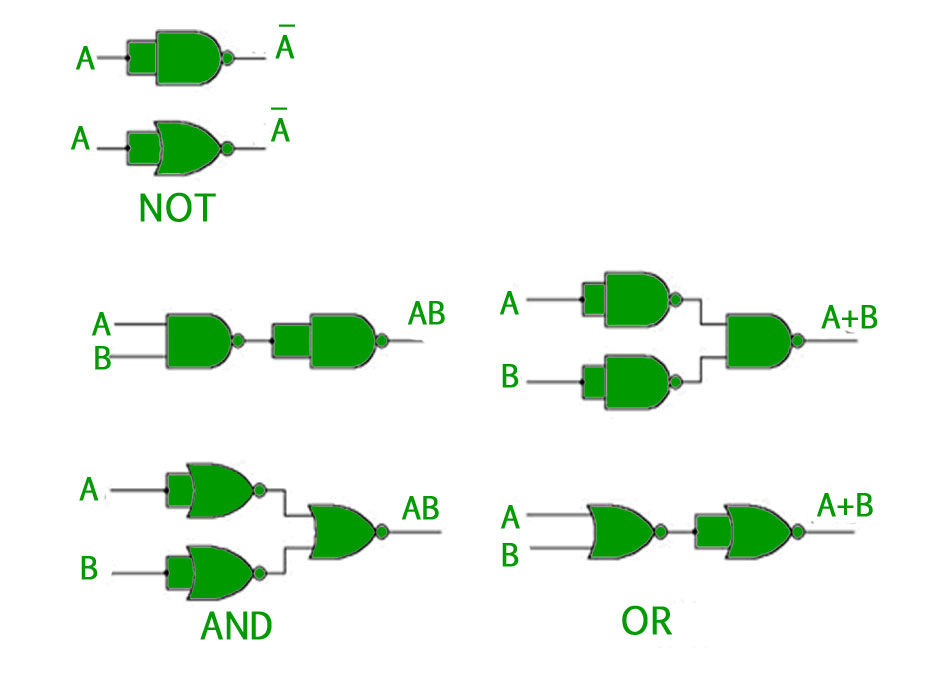 For the XOR gate, NAND and NOR implementation is –
For the XOR gate, NAND and NOR implementation is –
- Implemented Using NAND –

- Implemented using NOR –

Note – For implementing XNOR gate, a single NAND or NOR gate can be added to the above circuits to negate the output of the XOR gate.
GATE CS Corner Questions
Practicing the following questions will help you test your knowledge. All questions have been asked in GATE in previous years or in GATE Mock Tests. It is highly recommended that you practice them. 1. GATE CS 2013, Question 21 2. GATE CS 2012, Question 10 3. GATE CS 2007, Question 33 4. GATE CS 2005, Question 15
Reference –
Digital Design, 5th edition by Morris Mano and Michael Ciletti
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...