An interesting time complexity question

What is the time complexity of following function fun()?

int fun(int n)
{
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j < n; j += i)
        {
            // Some O(1) task
        }
    }
}

For i = 1, the inner loop is executed n times.
For i = 2, the inner loop is executed approximately n/2 times.
For i = 3, the inner loop is executed approximately n/3 times.
For i = 4, the inner loop is executed approximately n/4 times.
…………………………………………………….
…………………………………………………….
For i = n, the inner loop is executed approximately n/n times.

So the total time complexity of the above algorithm is (n + n/2 + n/3 + … + n/n)

Which becomes n * (1/1 + 1/2 + 1/3 + … + 1/n)

The important thing about series (1/1 + 1/2 + 1/3 + … + 1/n) is, it is equal to Θ(Logn) (See this for reference). So the time complexity of the above code is Θ(nLogn).

As a side note, the sum of infinite harmonic series is counterintuitive as the series diverges. The value of 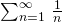is ∞. This is unlike geometric series as geometric series with ratio less than 1 converges.

Reference:
http://en.wikipedia.org/wiki/Harmonic_series_%28mathematics%29#Rate_of_divergence
http://staff.ustc.edu.cn/~csli/graduate/algorithms/book6/chap03.htm

This article is contributed by Rahul. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above

My Personal Notes arrow_drop_up

Save