Insertion sort is a simple sorting algorithm that works by iteratively inserting each element of an unsorted list into its correct position in a sorted portion of the list. It is a stable sorting algorithm, meaning that elements with equal values maintain their relative order in the sorted output.
Insertion sort is like sorting playing cards in your hands. You split the cards into two groups: the sorted cards and the unsorted cards. Then, you pick a card from the unsorted group and put it in the right place in the sorted group.
Insertion Sort Algorithm:
Insertion sort is a simple sorting algorithm that works by building a sorted array one element at a time. It is considered an "in-place" sorting algorithm, meaning it doesn't require any additional memory space beyond the original array.
Algorithm:
To achieve insertion sort, follow these steps:
- We have to start with second element of the array as first element in the array is assumed to be sorted.
- Compare second element with the first element and check if the second element is smaller then swap them.
- Move to the third element and compare it with the second element, then the first element and swap as necessary to put it in the correct position among the first three elements.
- Continue this process, comparing each element with the ones before it and swapping as needed to place it in the correct position among the sorted elements.
- Repeat until the entire array is sorted.
Working of Insertion Sort Algorithm:
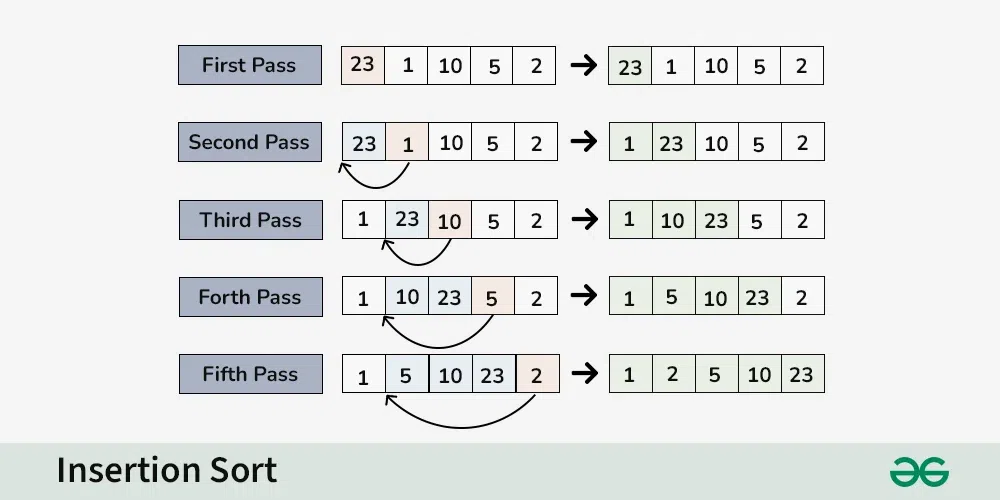
Consider an array having elements: {23, 1, 10, 5, 2}
First Pass:
- Current element is 23
- The first element in the array is assumed to be sorted.
- The sorted part until 0th index is : [23]
Second Pass:
- Compare 1 with 23 (current element with the sorted part).
- Since 1 is smaller, insert 1 before 23.
- The sorted part until 1st index is: [1, 23]
Third Pass:
- Compare 10 with 1 and 23 (current element with the sorted part).
- Since 10 is greater than 1 and smaller than 23, insert 10 between 1 and 23.
- The sorted part until 2nd index is: [1, 10, 23]
Fourth Pass:
- Compare 5 with 1, 10, and 23 (current element with the sorted part).
- Since 5 is greater than 1 and smaller than 10, insert 5 between 1 and 10.
- The sorted part until 3rd index is: [1, 5, 10, 23]
Fifth Pass:
- Compare 2 with 1, 5, 10, and 23 (current element with the sorted part).
- Since 2 is smaller than all elements in the sorted part, insert 2 at the beginning.
- The sorted part until 4th index is: [2, 1, 5, 10, 23]
Final Array:
- The sorted array is: [2, 1, 5, 10, 23]
Implementation of Insertion Sort:
// C++ program for insertion sort
#include <bits/stdc++.h>
using namespace std;
// Function to sort an array using
// insertion sort
void insertionSort(int arr[], int n)
{
int i, key, j;
for (i = 1; i < n; i++) {
key = arr[i];
j = i - 1;
// Move elements of arr[0..i-1],
// that are greater than key,
// to one position ahead of their
// current position
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
// A utility function to print an array
// of size n
void printArray(int arr[], int n)
{
int i;
for (i = 0; i < n; i++)
cout << arr[i] << " ";
cout << endl;
}
// Driver code
int main()
{
int arr[] = { 12, 11, 13, 5, 6 };
int N = sizeof(arr) / sizeof(arr[0]);
insertionSort(arr, N);
printArray(arr, N);
return 0;
}
// This is code is contributed by rathbhupendra
// C program for insertion sort
#include <math.h>
#include <stdio.h>
/* Function to sort an array using insertion sort*/
void insertionSort(int arr[], int n)
{
int i, key, j;
for (i = 1; i < n; i++) {
key = arr[i];
j = i - 1;
/* Move elements of arr[0..i-1], that are
greater than key, to one position ahead
of their current position */
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
// A utility function to print an array of size n
void printArray(int arr[], int n)
{
int i;
for (i = 0; i < n; i++)
printf("%d ", arr[i]);
printf("\n");
}
/* Driver program to test insertion sort */
int main()
{
int arr[] = { 12, 11, 13, 5, 6 };
int n = sizeof(arr) / sizeof(arr[0]);
insertionSort(arr, n);
printArray(arr, n);
return 0;
}
// Java program for implementation of Insertion Sort
public class InsertionSort {
/*Function to sort array using insertion sort*/
void sort(int arr[])
{
int n = arr.length;
for (int i = 1; i < n; ++i) {
int key = arr[i];
int j = i - 1;
/* Move elements of arr[0..i-1], that are
greater than key, to one position ahead
of their current position */
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
/* A utility function to print array of size n*/
static void printArray(int arr[])
{
int n = arr.length;
for (int i = 0; i < n; ++i)
System.out.print(arr[i] + " ");
System.out.println();
}
// Driver method
public static void main(String args[])
{
int arr[] = { 12, 11, 13, 5, 6 };
InsertionSort ob = new InsertionSort();
ob.sort(arr);
printArray(arr);
}
};
/* This code is contributed by Rajat Mishra. */
# Python program for implementation of Insertion Sort
# Function to do insertion sort
def insertionSort(arr):
# Traverse through 1 to len(arr)
for i in range(1, len(arr)):
key = arr[i]
# Move elements of arr[0..i-1], that are
# greater than key, to one position ahead
# of their current position
j = i-1
while j >= 0 and key < arr[j] :
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
# Driver code to test above
arr = [12, 11, 13, 5, 6]
insertionSort(arr)
for i in range(len(arr)):
print ("% d" % arr[i])
# This code is contributed by Mohit Kumra
// C# program for implementation of Insertion Sort
using System;
class InsertionSort {
// Function to sort array
// using insertion sort
void sort(int[] arr)
{
int n = arr.Length;
for (int i = 1; i < n; ++i) {
int key = arr[i];
int j = i - 1;
// Move elements of arr[0..i-1],
// that are greater than key,
// to one position ahead of
// their current position
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
// A utility function to print
// array of size n
static void printArray(int[] arr)
{
int n = arr.Length;
for (int i = 0; i < n; ++i)
Console.Write(arr[i] + " ");
Console.Write("\n");
}
// Driver Code
public static void Main()
{
int[] arr = { 12, 11, 13, 5, 6 };
InsertionSort ob = new InsertionSort();
ob.sort(arr);
printArray(arr);
}
}
// This code is contributed by ChitraNayal.
<script>
// Javascript program for insertion sort
// Function to sort an array using insertion sort
function insertionSort(arr, n)
{
let i, key, j;
for (i = 1; i < n; i++)
{
key = arr[i];
j = i - 1;
/* Move elements of arr[0..i-1], that are
greater than key, to one position ahead
of their current position */
while (j >= 0 && arr[j] > key)
{
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
// A utility function to print an array of size n
function printArray(arr, n)
{
let i;
for (i = 0; i < n; i++)
document.write(arr[i] + " ");
document.write("<br>");
}
// Driver code
let arr = [12, 11, 13, 5, 6 ];
let n = arr.length;
insertionSort(arr, n);
printArray(arr, n);
// This code is contributed by Mayank Tyagi
</script>
<?php
// PHP program for insertion sort
// Function to sort an array
// using insertion sort
function insertionSort(&$arr, $n)
{
for ($i = 1; $i < $n; $i++)
{
$key = $arr[$i];
$j = $i-1;
// Move elements of arr[0..i-1],
// that are greater than key, to
// one position ahead of their
// current position
while ($j >= 0 && $arr[$j] > $key)
{
$arr[$j + 1] = $arr[$j];
$j = $j - 1;
}
$arr[$j + 1] = $key;
}
}
// A utility function to
// print an array of size n
function printArray(&$arr, $n)
{
for ($i = 0; $i < $n; $i++)
echo $arr[$i]." ";
echo "\n";
}
// Driver Code
$arr = array(12, 11, 13, 5, 6);
$n = sizeof($arr);
insertionSort($arr, $n);
printArray($arr, $n);
// This code is contributed by ChitraNayal.
?>
Output
5 6 11 12 13
Time Complexity: O(N^2)
Auxiliary Space: O(1)
Complexity Analysis of Insertion Sort:
Time Complexity of Insertion Sort
- Best case: O(n), If the list is already sorted, where n is the number of elements in the list.
- Average case: O(n2), If the list is randomly ordered
- Worst case: O(n2), If the list is in reverse order
Space Complexity of Insertion Sort
- Auxiliary Space: O(1), Insertion sort requires O(1) additional space, making it a space-efficient sorting algorithm.
Advantages of Insertion Sort:
- Simple and easy to implement.
- Stable sorting algorithm.
- Efficient for small lists and nearly sorted lists.
- Space-efficient.
Disadvantages of Insertion Sort:
- Inefficient for large lists.
- Not as efficient as other sorting algorithms (e.g., merge sort, quick sort) for most cases.
Applications of Insertion Sort:
Insertion sort is commonly used in situations where:
- The list is small or nearly sorted.
- Simplicity and stability are important.
Frequently Asked Questions on Insertion Sort
Q1. What are the Boundary Cases of the Insertion Sort algorithm?
Insertion sort takes the maximum time to sort if elements are sorted in reverse order. And it takes minimum time (Order of n) when elements are already sorted.
Q2. What is the Algorithmic Paradigm of the Insertion Sort algorithm?
The Insertion Sort algorithm follows an incremental approach.
Q3. Is Insertion Sort an in-place sorting algorithm?
Yes, insertion sort is an in-place sorting algorithm.
Q4. Is Insertion Sort a stable algorithm?
Yes, insertion sort is a stable sorting algorithm.
Q5. When is the Insertion Sort algorithm used?
Insertion sort is used when number of elements is small. It can also be useful when the input array is almost sorted, and only a few elements are misplaced in a complete big array.