Prerequisite: Introduction of B+ trees
In this article, we will discuss that how to insert a node in B+ Tree. During insertion following properties of B+ Tree must be followed:
- Each node except root can have a maximum of M children and at least ceil(M/2) children.
- Each node can contain a maximum of M - 1 keys and a minimum of ceil(M/2) - 1 keys.
- The root has at least two children and atleast one search key.
- While insertion overflow of the node occurs when it contains more than M - 1 search key values.
Here M is the order of B+ tree.
Steps for insertion in B+ Tree
- Every element is inserted into a leaf node. So, go to the appropriate leaf node.
- Insert the key into the leaf node in increasing order only if there is no overflow. If there is an overflow go ahead with the following steps mentioned below to deal with overflow while maintaining the B+ Tree properties.
Properties for insertion B+ Tree
Case 1: Overflow in leaf node
- Split the leaf node into two nodes.
- First node contains ceil((m-1)/2) values.
- Second node contains the remaining values.
- Copy the smallest search key value from second node to the parent node.(Right biased)
Below is the illustration of inserting 8 into B+ Tree of order of 5:
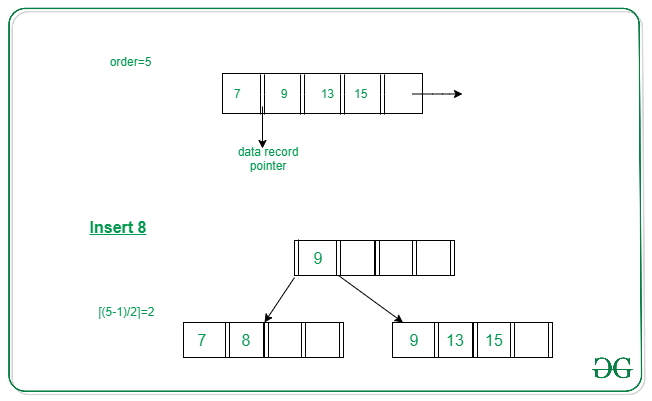
Case 2: Overflow in non-leaf node
- Split the non leaf node into two nodes.
- First node contains ceil(m/2)-1 values.
- Move the smallest among remaining to the parent.
- Second node contains the remaining keys.
Below is the illustration of inserting 15 into B+ Tree of order of 5:

Example to illustrate insertion on a B+ tree
Problem: Insert the following key values 6, 16, 26, 36, 46 on a B+ tree with order = 3.
Solution:
Step 1: The order is 3 so at maximum in a node so there can be only 2 search key values. As insertion happens on a leaf node only in a B+ tree so insert search key value 6 and 16 in increasing order in the node. Below is the illustration of the same:

Step 2: We cannot insert 26 in the same node as it causes an overflow in the leaf node, We have to split the leaf node according to the rules. First part contains ceil((3-1)/2) values i.e., only 6. The second node contains the remaining values i.e., 16 and 26. Then also copy the smallest search key value from the second node to the parent node i.e., 16 to the parent node. Below is the illustration of the same:

Step 3: Now the next value is 36 that is to be inserted after 26 but in that node, it causes an overflow again in that leaf node. Again follow the above steps to split the node. First part contains ceil((3-1)/2) values i.e., only 16. The second node contains the remaining values i.e., 26 and 36. Then also copy the smallest search key value from the second node to the parent node i.e., 26 to the parent node. Below is the illustration of the same:
The illustration is shown in the diagram below.

Step 4: Now we have to insert 46 which is to be inserted after 36 but it causes an overflow in the leaf node. So we split the node according to the rules. The first part contains 26 and the second part contains 36 and 46 but now we also have to copy 36 to the parent node but it causes overflow as only two search key values can be accommodated in a node. Now follow the steps to deal with overflow in the non-leaf node.
First node contains ceil(3/2)-1 values i.e. '16'.
Move the smallest among remaining to the parent i.e '26' will be the new parent node.
The second node contains the remaining keys i.e '36' and the rest of the leaf nodes remain the same. Below is the illustration of the same:

Below is the python implementation of B+ tree:
#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
using namespace std;
// Node class
class Node {
public:
int t; // Order of the B+ tree
vector<string> keys; // Keys in the node
vector<vector<int>> values;
vector<Node*> child_ptr; // Pointers to child nodes
bool leaf; // Boolean to check if the node is a leaf
int n; // Current number of keys
Node* ptr2next; // Pointer to the next node
// Node constructor
Node(int _t, Node* _ptr2next = NULL) {
t = _t;
ptr2next = _ptr2next;
leaf = true;
keys.resize(2*t-1);
values.resize(2*t-1);
child_ptr.resize(2*t);
n = 0;
}
// Function to insert a key in a non-full node
void insertNonFull(string k, int v) {
int i = n-1;
if (leaf) {
keys.insert(keys.begin()+n, k);
values.insert(values.begin()+n, vector<int>(1, v));
n += 1;
while (i>=0 && keys[i]>k) {
swap(keys[i], keys[i+1]);
swap(values[i], values[i+1]);
i -= 1;
}
} else {
while (i>=0 && keys[i]>k) {
i -= 1;
}
i += 1;
if (child_ptr[i]->n == 2*t-1) {
splitChild(i);
if (keys[i] < k) {
i += 1;
}
}
child_ptr[i]->insertNonFull(k, v);
}
}
// Function to split the child
void splitChild(int i) {
Node* y = child_ptr[i];
Node* z = new Node(y->t, y->ptr2next);
child_ptr.insert(child_ptr.begin()+i+1, z);
keys.insert(keys.begin()+i, y->keys[t-1]);
values.insert(values.begin()+i, y->values[t-1]);
y->ptr2next = z;
z->leaf = y->leaf;
z->n = t-1;
y->n = t-1;
for (int j=0; j<t-1; j++) {
z->keys[j] = y->keys[j+t];
z->values[j] = y->values[j+t];
}
if (!y->leaf) {
for (int j=0; j<t; j++) {
z->child_ptr[j] = y->child_ptr[j+t];
}
}
n += 1;
}
// Function to print the tree
void print() {
for (int i=0; i<n; i++) {
if (!leaf) {
child_ptr[i]->print();
}
cout << "['" << keys[i] << "']" << endl;
}
if (!leaf) {
child_ptr[n]->print();
}
}
// Function to search a key in the tree
Node* search(string k, int v) {
int i = 0;
while (i<n && k>keys[i]) {
i += 1;
}
if (keys[i] == k) {
for (int j = 0; j < values[i].size(); j++) {
if (values[i][j] == v) {
return this;
}
}
}
if (leaf) {
return NULL;
} else {
return child_ptr[i]->search(k, v);
}
}
};
class BTree {
public:
Node* root; // Root of the B+ tree
int t; // Order of the B+ tree
// BTree constructor
BTree(int _t) {
root = new Node(_t);
root->leaf = true;
}
// Function to insert a key in the tree
void insert(string k, int v) {
Node* r = root;
if (r->n == 2*t-1) {
Node* s = new Node(t);
root = s;
s->child_ptr[0] = r;
s->splitChild(0);
s->insertNonFull(k, v);
} else {
r->insertNonFull(k, v);
}
}
// Function to print the tree
void print() {
root->print();
}
// Function to search a key in the tree
Node* search(string k, int v) {
return (root == NULL)? NULL : root->search(k, v);
}
};
// Function to print the tree
void printTree(BTree* tree) {
tree->print();
}
int main() {
int record_len = 3;
BTree* bplustree = new BTree(record_len);
bplustree->insert("5", 33);
bplustree->insert("15", 21);
bplustree->insert("25", 31);
bplustree->insert("35", 41);
bplustree->insert("45", 10);
printTree(bplustree);
if (bplustree->search("5", 34) != NULL) {
cout << "Found" << endl;
} else {
cout << "Not found" << endl;
}
return 0;
}
import java.util.ArrayList;
import java.util.List;
// Node creation
class Node {
int order;
List<String> values;
List<List<Node>> keys;
Node nextKey;
Node parent;
boolean isLeaf;
// Node constructor
public Node(int order) {
this.order = order;
this.values = new ArrayList<>();
this.keys = new ArrayList<>();
this.nextKey = null;
this.parent = null;
this.isLeaf = false;
}
// Insert at the leaf
public void insertAtLeaf(String value, Node key) {
if (!this.values.isEmpty()) {
for (int i = 0; i < this.values.size(); i++) {
if (value.equals(this.values.get(i))) {
this.keys.get(i).add(key);
break;
} else if (value.compareTo(this.values.get(i)) < 0) {
this.values.add(i, value);
this.keys.add(i, new ArrayList<>());
this.keys.get(i).add(key);
break;
} else if (i + 1 == this.values.size()) {
this.values.add(value);
this.keys.add(new ArrayList<>());
this.keys.get(i + 1).add(key);
break;
}
}
} else {
this.values.add(value);
this.keys.add(new ArrayList<>());
this.keys.get(0).add(key);
}
}
}
// B plus tree
class BplusTree {
Node root;
// B plus tree constructor
public BplusTree(int order) {
this.root = new Node(order);
this.root.isLeaf = true;
}
// Insert operation
public void insert(String value, Node key) {
Node oldNode = this.search(value);
oldNode.insertAtLeaf(value, key);
if (oldNode.values.size() == oldNode.order) {
Node newNode = new Node(oldNode.order);
newNode.isLeaf = true;
newNode.parent = oldNode.parent;
int mid = (int) Math.ceil(oldNode.order / 2.0) - 1;
newNode.values = new ArrayList<>(oldNode.values.subList(mid + 1, oldNode.values.size()));
newNode.keys = new ArrayList<>(oldNode.keys.subList(mid + 1, oldNode.keys.size()));
newNode.nextKey = oldNode.nextKey;
oldNode.values = new ArrayList<>(oldNode.values.subList(0, mid + 1));
oldNode.keys = new ArrayList<>(oldNode.keys.subList(0, mid + 1));
oldNode.nextKey = newNode;
this.insertInParent(oldNode, newNode.values.get(0), newNode);
}
}
// Search operation for different operations
public Node search(String value) {
Node currentNode = this.root;
while (!currentNode.isLeaf) {
for (int i = 0; i < currentNode.values.size(); i++) {
if (value.equals(currentNode.values.get(i))) {
currentNode = currentNode.keys.get(i + 1).get(0);
break;
} else if (value.compareTo(currentNode.values.get(i)) < 0) {
currentNode = currentNode.keys.get(i).get(0);
break;
} else if (i + 1 == currentNode.values.size()) {
currentNode = currentNode.keys.get(i + 1).get(0);
break;
}
}
}
return currentNode;
}
// Find the node
public boolean find(String value, Node key) {
Node leaf = this.search(value);
for (int i = 0; i < leaf.values.size(); i++) {
if (leaf.values.get(i).equals(value)) {
if (leaf.keys.get(i).contains(key)) {
return true;
} else {
return false;
}
}
}
return false;
}
// Inserting at the parent
public void insertInParent(Node n, String value, Node ndash) {
if (this.root == n) {
Node rootNode = new Node(n.order);
rootNode.values.add(value);
rootNode.keys.add(new ArrayList<>());
rootNode.keys.add(new ArrayList<>());
rootNode.keys.get(0).add(n);
rootNode.keys.get(1).add(ndash);
this.root = rootNode;
n.parent = rootNode;
ndash.parent = rootNode;
return;
}
Node parentNode = n.parent;
for (int i = 0; i < parentNode.keys.size(); i++) {
if (parentNode.keys.get(i).get(0) == n) {
parentNode.values.add(i, value);
parentNode.keys.add(i + 1, new ArrayList<>());
parentNode.keys.get(i + 1).add(ndash);
if (parentNode.keys.size() > parentNode.order) {
Node parentdash = new Node(parentNode.order);
parentdash.parent = parentNode.parent;
int mid = (int) Math.ceil(parentNode.order / 2.0) - 1;
parentdash.values = new ArrayList<>(parentNode.values.subList(mid + 1, parentNode.values.size()));
parentdash.keys = new ArrayList<>(parentNode.keys.subList(mid + 1, parentNode.keys.size()));
String value_ = parentNode.values.get(mid);
if (mid == 0) {
parentNode.values = new ArrayList<>(parentNode.values.subList(0, mid + 1));
} else {
parentNode.values = new ArrayList<>(parentNode.values.subList(0, mid));
}
parentNode.keys = new ArrayList<>(parentNode.keys.subList(0, mid + 1));
for (int j = 0; j < parentNode.keys.size(); j++) {
parentNode.keys.get(j).get(0).parent = parentNode;
}
for (int j = 0; j < parentdash.keys.size(); j++) {
parentdash.keys.get(j).get(0).parent = parentdash;
}
this.insertInParent(parentNode, value_, parentdash);
}
break;
}
}
}
}
public class Main {
public static void main(String[] args) {
BplusTree bplusTree = new BplusTree(3);
bplusTree.insert("5", new Node(3));
bplusTree.insert("15", new Node(3));
bplusTree.insert("25", new Node(3));
bplusTree.insert("35", new Node(3));
bplusTree.insert("45", new Node(3));
printTree(bplusTree);
if (bplusTree.find("5", new Node(3))) {
System.out.println("Found");
} else {
System.out.println("Not found");
}
}
// Print the tree
public static void printTree(BplusTree tree) {
List<Node> lst = new ArrayList<>();
lst.add(tree.root);
List<Integer> level = new ArrayList<>();
level.add(0);
Node leaf = null;
int flag = 0;
int lev_leaf = 0;
while (!lst.isEmpty()) {
Node x = lst.remove(0);
int lev = level.remove(0);
if (!x.isLeaf) {
for (int i = 0; i < x.keys.size(); i++) {
System.out.println(x.keys.get(i).get(0).values);
}
} else {
for (int i = 0; i < x.keys.size(); i++) {
System.out.println(x.keys.get(i).get(0).values);
}
if (flag == 0) {
lev_leaf = lev;
leaf = x;
flag = 1;
}
}
}
}
}
# Python3 program for implementing B+ Tree
import math
# Node creation
class Node:
def __init__(self, order):
self.order = order
self.values = []
self.keys = []
self.nextKey = None
self.parent = None
self.check_leaf = False
# Insert at the leaf
def insert_at_leaf(self, leaf, value, key):
if (self.values):
temp1 = self.values
for i in range(len(temp1)):
if (value == temp1[i]):
self.keys[i].append(key)
break
elif (value < temp1[i]):
self.values = self.values[:i] + [value] + self.values[i:]
self.keys = self.keys[:i] + [[key]] + self.keys[i:]
break
elif (i + 1 == len(temp1)):
self.values.append(value)
self.keys.append([key])
break
else:
self.values = [value]
self.keys = [[key]]
# B plus tree
class BplusTree:
def __init__(self, order):
self.root = Node(order)
self.root.check_leaf = True
# Insert operation
def insert(self, value, key):
value = str(value)
old_node = self.search(value)
old_node.insert_at_leaf(old_node, value, key)
if (len(old_node.values) == old_node.order):
node1 = Node(old_node.order)
node1.check_leaf = True
node1.parent = old_node.parent
mid = int(math.ceil(old_node.order / 2)) - 1
node1.values = old_node.values[mid + 1:]
node1.keys = old_node.keys[mid + 1:]
node1.nextKey = old_node.nextKey
old_node.values = old_node.values[:mid + 1]
old_node.keys = old_node.keys[:mid + 1]
old_node.nextKey = node1
self.insert_in_parent(old_node, node1.values[0], node1)
# Search operation for different operations
def search(self, value):
current_node = self.root
while(current_node.check_leaf == False):
temp2 = current_node.values
for i in range(len(temp2)):
if (value == temp2[i]):
current_node = current_node.keys[i + 1]
break
elif (value < temp2[i]):
current_node = current_node.keys[i]
break
elif (i + 1 == len(current_node.values)):
current_node = current_node.keys[i + 1]
break
return current_node
# Find the node
def find(self, value, key):
l = self.search(value)
for i, item in enumerate(l.values):
if item == value:
if key in l.keys[i]:
return True
else:
return False
return False
# Inserting at the parent
def insert_in_parent(self, n, value, ndash):
if (self.root == n):
rootNode = Node(n.order)
rootNode.values = [value]
rootNode.keys = [n, ndash]
self.root = rootNode
n.parent = rootNode
ndash.parent = rootNode
return
parentNode = n.parent
temp3 = parentNode.keys
for i in range(len(temp3)):
if (temp3[i] == n):
parentNode.values = parentNode.values[:i] + \
[value] + parentNode.values[i:]
parentNode.keys = parentNode.keys[:i +
1] + [ndash] + parentNode.keys[i + 1:]
if (len(parentNode.keys) > parentNode.order):
parentdash = Node(parentNode.order)
parentdash.parent = parentNode.parent
mid = int(math.ceil(parentNode.order / 2)) - 1
parentdash.values = parentNode.values[mid + 1:]
parentdash.keys = parentNode.keys[mid + 1:]
value_ = parentNode.values[mid]
if (mid == 0):
parentNode.values = parentNode.values[:mid + 1]
else:
parentNode.values = parentNode.values[:mid]
parentNode.keys = parentNode.keys[:mid + 1]
for j in parentNode.keys:
j.parent = parentNode
for j in parentdash.keys:
j.parent = parentdash
self.insert_in_parent(parentNode, value_, parentdash)
# Print the tree
def printTree(tree):
lst = [tree.root]
level = [0]
leaf = None
flag = 0
lev_leaf = 0
node1 = Node(str(level[0]) + str(tree.root.values))
while (len(lst) != 0):
x = lst.pop(0)
lev = level.pop(0)
if (x.check_leaf == False):
for i, item in enumerate(x.keys):
print(item.values)
else:
for i, item in enumerate(x.keys):
print(item.values)
if (flag == 0):
lev_leaf = lev
leaf = x
flag = 1
record_len = 3
bplustree = BplusTree(record_len)
bplustree.insert('5', '33')
bplustree.insert('15', '21')
bplustree.insert('25', '31')
bplustree.insert('35', '41')
bplustree.insert('45', '10')
printTree(bplustree)
if(bplustree.find('5', '34')):
print("Found")
else:
print("Not found")
using System;
using System.Collections.Generic;
public class Node
{
public int t; // Order of the B+ tree
public List<string> keys; // Keys in the node
public List<List<int>> values;
public List<Node> child_ptr; // Pointers to child nodes
public bool leaf; // Boolean to check if the node is a leaf
public int n; // Current number of keys
public Node ptr2next; // Pointer to the next node
// Node constructor
public Node(int _t, Node _ptr2next = null)
{
t = _t;
ptr2next = _ptr2next;
leaf = true;
keys = new List<string>(2 * t - 1);
values = new List<List<int>>(2 * t - 1);
child_ptr = new List<Node>(2 * t);
n = 0;
}
// Function to insert a key in a non-full node
public void InsertNonFull(string k, int v)
{
int i = n - 1;
if (leaf)
{
keys.Insert(n, k);
values.Insert(n, new List<int> { v });
n += 1;
while (i >= 0 && string.Compare(keys[i], k) > 0)
{
string tempKey = keys[i];
keys[i] = keys[i + 1];
keys[i + 1] = tempKey;
List<int> tempValue = values[i];
values[i] = values[i + 1];
values[i + 1] = tempValue;
i -= 1;
}
}
else
{
while (i >= 0 && string.Compare(keys[i], k) > 0)
{
i -= 1;
}
i += 1;
if (child_ptr[i].n == 2 * t - 1)
{
SplitChild(i);
if (string.Compare(keys[i], k) < 0)
{
i += 1;
}
}
child_ptr[i].InsertNonFull(k, v);
}
}
// Function to split the child
public void SplitChild(int i)
{
Node y = child_ptr[i];
Node z = new Node(y.t, y.ptr2next);
child_ptr.Insert(i + 1, z);
keys.Insert(i, y.keys[t - 1]);
values.Insert(i, y.values[t - 1]);
y.ptr2next = z;
z.leaf = y.leaf;
z.n = t - 1;
y.n = t - 1;
for (int j = 0; j < t - 1; j++)
{
z.keys[j] = y.keys[j + t];
z.values[j] = y.values[j + t];
}
if (!y.leaf)
{
for (int j = 0; j < t; j++)
{
z.child_ptr[j] = y.child_ptr[j + t];
}
}
n += 1;
}
// Function to print the tree
public void Print()
{
for (int i = 0; i < n; i++)
{
if (!leaf)
{
child_ptr[i].Print();
}
Console.WriteLine("['" + keys[i] + "']");
}
if (!leaf)
{
child_ptr[n].Print();
}
}
// Function to search a key in the tree
public Node Search(string k, int v)
{
int i = 0;
while (i < n && string.Compare(keys[i], k) < 0)
{
i += 1;
}
if (keys[i] == k)
{
for (int j = 0; j < values[i].Count; j++)
{
if (values[i][j] == v)
{
return this;
}
}
}
if (leaf)
{
return null;
}
else
{
return child_ptr[i].Search(k, v);
}
}
}
public class BTree
{
public Node root; // Root of the B+ tree
public int t; // Order of the B+ tree
// BTree constructor
public BTree(int _t)
{
root = new Node(_t);
root.leaf = true;
t = _t;
}
// Function to insert a key in the tree
public void Insert(string k, int v)
{
Node r = root;
if (r.n == 2 * t - 1)
{
Node s = new Node(t);
root = s;
s.child_ptr.Add(r);
s.SplitChild(0);
s.InsertNonFull(k, v);
}
else
{
r.InsertNonFull(k, v);
}
}
// Function to print the tree
public void Print()
{
root.Print();
}
// Function to search a key in the tree
public Node Search(string k, int v)
{
return (root == null) ? null : root.Search(k, v);
}
}
public class Program
{
// Function to print the tree
public static void PrintTree(BTree tree)
{
tree.Print();
}
public static void Main()
{
int record_len = 3;
BTree bplustree = new BTree(record_len);
bplustree.Insert("5", 33);
bplustree.Insert("15", 21);
bplustree.Insert("25", 31);
bplustree.Insert("35", 41);
bplustree.Insert("45", 10);
PrintTree(bplustree);
if (bplustree.Search("5", 34) != null)
{
Console.WriteLine("Found");
}
else
{
Console.WriteLine("Not found");
}
}
}
// JavaScript equivalent
// Node creation
class Node {
constructor(order) {
this.order = order;
this.values = [];
this.keys = [];
this.nextKey = null;
this.parent = null;
this.check_leaf = false;
}
// Insert at the leaf
insert_at_leaf(leaf, value, key) {
if (this.values.length !== 0) {
const temp1 = this.values;
for (let i = 0; i < temp1.length; i++) {
if (value == temp1[i]) {
this.keys[i].push(key);
break;
} else if (value < temp1[i]) {
this.values = [
...this.values.slice(0, i),
value,
...this.values.slice(i)
];
this.keys = [
...this.keys.slice(0, i),
[key],
...this.keys.slice(i)
];
break;
} else if (i + 1 == temp1.length) {
this.values.push(value);
this.keys.push([key]);
break;
}
}
} else {
this.values = [value];
this.keys = [[key]];
}
}
}
// B plus tree
class BplusTree {
constructor(order) {
this.root = new Node(order);
this.root.check_leaf = true;
}
// Insert operation
insert(value, key) {
value = String(value);
const old_node = this.search(value);
old_node.insert_at_leaf(old_node, value, key);
if (old_node.values.length == old_node.order) {
const node1 = new Node(old_node.order);
node1.check_leaf = true;
node1.parent = old_node.parent;
const mid = Math.ceil(old_node.order / 2) - 1;
node1.values = old_node.values.slice(mid + 1);
node1.keys = old_node.keys.slice(mid + 1);
node1.nextKey = old_node.nextKey;
old_node.values = old_node.values.slice(0, mid + 1);
old_node.keys = old_node.keys.slice(0, mid + 1);
old_node.nextKey = node1;
this.insert_in_parent(old_node, node1.values[0], node1);
}
}
// Search operation for different operations
search(value) {
let current_node = this.root;
while (current_node.check_leaf == false) {
const temp2 = current_node.values;
for (let i = 0; i < temp2.length; i++) {
if (value == temp2[i]) {
current_node = current_node.keys[i + 1];
break;
} else if (value < temp2[i]) {
current_node = current_node.keys[i];
break;
} else if (i + 1 == current_node.values.length) {
current_node = current_node.keys[i + 1];
break;
}
}
}
return current_node;
}
// Find the node
find(value, key) {
const l = this.search(value);
for (let i = 0; i < l.values.length; i++) {
if (l.values[i] == value) {
if (l.keys[i].includes(key)) {
return true;
} else {
return false;
}
}
}
return false;
}
// Inserting at the parent
insert_in_parent(n, value, ndash) {
if (this.root == n) {
const rootNode = new Node(n.order);
rootNode.values = [value];
rootNode.keys = [n, ndash];
this.root = rootNode;
n.parent = rootNode;
ndash.parent = rootNode;
return;
}
const parentNode = n.parent;
const temp3 = parentNode.keys;
for (let i = 0; i < temp3.length; i++) {
if (temp3[i] == n) {
parentNode.values = [
...parentNode.values.slice(0, i),
value,
...parentNode.values.slice(i)
];
parentNode.keys = [
...parentNode.keys.slice(0, i + 1),
ndash,
...parentNode.keys.slice(i + 1)
];
if (parentNode.keys.length > parentNode.order) {
const parentdash = new Node(parentNode.order);
parentdash.parent = parentNode.parent;
const mid = Math.ceil(parentNode.order / 2) - 1;
parentdash.values = parentNode.values.slice(mid + 1);
parentdash.keys = parentNode.keys.slice(mid + 1);
const value_ = parentNode.values[mid];
if (mid == 0) {
parentNode.values = parentNode.values.slice(0, mid + 1);
} else {
parentNode.values = parentNode.values.slice(0, mid);
}
parentNode.keys = parentNode.keys.slice(0, mid + 1);
for (let j = 0; j < parentNode.keys.length; j++) {
parentNode.keys[j].parent = parentNode;
}
for (let j = 0; j < parentdash.keys.length; j++) {
parentdash.keys[j].parent = parentdash;
}
this.insert_in_parent(parentNode, value_, parentdash);
}
}
}
}
}
// Print the tree
function printTree(tree) {
let lst = [tree.root];
let level = [0];
let leaf = null;
let flag = 0;
let lev_leaf = 0;
const node1 = new Node(String(level[0]) + String(tree.root.values));
while (lst.length !== 0) {
const x = lst.shift();
const lev = level.shift();
if (x.check_leaf == false) {
for (let i = 0; i < x.keys.length; i++) {
console.log(x.keys[i].values);
}
} else {
for (let i = 0; i < x.keys.length; i++) {
console.log(x.keys[i].values);
}
if (flag == 0) {
lev_leaf = lev;
leaf = x;
flag = 1;
}
}
}
}
const record_len = 3;
const bplustree = new BplusTree(record_len);
bplustree.insert("5", "33");
bplustree.insert("15", "21");
bplustree.insert("25", "31");
bplustree.insert("35", "41");
bplustree.insert("45", "10");
printTree(bplustree);
if (bplustree.find("5", "34")) {
console.log("Found");
} else {
console.log("Not found");
}
Output
['15'] ['25'] ['35'] ['45'] ['5'] Not found
Time complexity: O(log n)
Auxiliary Space: O(log n)
Below is the C++ implementation B+ tree:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define pb push_back
int bucketSize = 3;
// Create 2 classes, one for node and one for tree;
class node {
public:
bool isLeaf;
node** ptr;
int *key, size;
node();
};
node::node()
{
key = new int[bucketSize];
ptr = new node*[bucketSize + 1]();
}
class Btree {
public:
// Root of tree stored here;
node* root;
Btree();
void deleteNode(int);
int search(int);
void display(node*);
void insert(int);
node* findParent(node*, node*);
node* getRoot();
void shiftLevel(int, node*, node*);
};
node* Btree::getRoot() { return root; }
Btree::Btree() { root = NULL; }
void Btree::insert(int x)
{
if (root == NULL) {
root = new node;
root->key[0] = x;
root->isLeaf = true;
root->size = 1;
}
else {
node* current = root;
node* parent;
while (current->isLeaf == false) {
parent = current;
for (int i = 0; i < current->size; i++) {
if (x < current->key[i]) {
current = current->ptr[i];
break;
}
if (i == current->size - 1) {
current = current->ptr[i + 1];
break;
}
}
}
// now we have reached leaf;
if (current->size
< bucketSize) { // if the node to be inserted is
// not filled
int i = 0;
// Traverse btree
while (x > current->key[i] && i < current->size)
// goto pt where needs to be inserted.
i++;
for (int j = current->size; j > i; j--)
// adjust and insert element;
current->key[j] = current->key[j - 1];
current->key[i] = x;
// size should be increased by 1
current->size++;
current->ptr[current->size]
= current->ptr[current->size - 1];
current->ptr[current->size - 1] = NULL;
}
// if block does not have enough space;
else {
node* newLeaf = new node;
int tempNode[bucketSize + 1];
for (int i = 0; i < bucketSize; i++)
// all elements of this block stored
tempNode[i] = current->key[i];
int i = 0, j;
// find the right posn of num to be inserted
while (x > tempNode[i] && i < bucketSize)
i++;
for (int j = bucketSize + 1; j > i; j--)
tempNode[j] = tempNode[j - 1];
tempNode[i] = x;
// inserted element in its rightful position;
newLeaf->isLeaf = true;
current->size = (bucketSize + 1) / 2;
newLeaf->size
= (bucketSize + 1)
- (bucketSize + 1)
/ 2; // now rearrangement begins!
current->ptr[current->size] = newLeaf;
newLeaf->ptr[newLeaf->size]
= current->ptr[bucketSize];
current->ptr[newLeaf->size]
= current->ptr[bucketSize];
current->ptr[bucketSize] = NULL;
for (int i = 0; i < current->size; i++)
current->key[i] = tempNode[i];
for (int i = 0, j = current->size;
i < newLeaf->size; i++, j++)
newLeaf->key[i] = tempNode[j];
// if this is root, then fine,
// else we need to increase the height of tree;
if (current == root) {
node* newRoot = new node;
newRoot->key[0] = newLeaf->key[0];
newRoot->ptr[0] = current;
newRoot->ptr[1] = newLeaf;
newRoot->isLeaf = false;
newRoot->size = 1;
root = newRoot;
}
else
shiftLevel(
newLeaf->key[0], parent,
newLeaf); // parent->original root
}
}
}
void Btree::shiftLevel(int x, node* current, node* child)
{ // insert or create an internal node;
if (current->size
< bucketSize) { // if can fit in this level, do that
int i = 0;
while (x > current->key[i] && i < current->size)
i++;
for (int j = current->size; j > i; j--)
current->key[j] = current->key[j - 1];
for (int j = current->size + 1; j > i + 1; j--)
current->ptr[j] = current->ptr[j - 1];
current->key[i] = x;
current->size++;
current->ptr[i + 1] = child;
}
// shift up
else {
node* newInternal = new node;
int tempKey[bucketSize + 1];
node* tempPtr[bucketSize + 2];
for (int i = 0; i < bucketSize; i++)
tempKey[i] = current->key[i];
for (int i = 0; i < bucketSize + 1; i++)
tempPtr[i] = current->ptr[i];
int i = 0, j;
while (x > tempKey[i] && i < bucketSize)
i++;
for (int j = bucketSize + 1; j > i; j--)
tempKey[j] = tempKey[j - 1];
tempKey[i] = x;
for (int j = bucketSize + 2; j > i + 1; j--)
tempPtr[j] = tempPtr[j - 1];
tempPtr[i + 1] = child;
newInternal->isLeaf = false;
current->size = (bucketSize + 1) / 2;
newInternal->size
= bucketSize - (bucketSize + 1) / 2;
for (int i = 0, j = current->size + 1;
i < newInternal->size; i++, j++)
newInternal->key[i] = tempKey[j];
for (int i = 0, j = current->size + 1;
i < newInternal->size + 1; i++, j++)
newInternal->ptr[i] = tempPtr[j];
if (current == root) {
node* newRoot = new node;
newRoot->key[0] = current->key[current->size];
newRoot->ptr[0] = current;
newRoot->ptr[1] = newInternal;
newRoot->isLeaf = false;
newRoot->size = 1;
root = newRoot;
}
else
shiftLevel(current->key[current->size],
findParent(root, current),
newInternal);
}
}
int Btree::search(int x)
{
if (root == NULL)
return -1;
else {
node* current = root;
while (current->isLeaf == false) {
for (int i = 0; i < current->size; i++) {
if (x < current->key[i]) {
current = current->ptr[i];
break;
}
if (i == current->size - 1) {
current = current->ptr[i + 1];
break;
}
}
}
for (int i = 0; i < current->size; i++) {
if (current->key[i] == x) {
// cout<<"Key found "<<endl;
return 1;
// return;
}
}
// cout<<"Key not found"<<endl;
return 0;
}
}
// Print the tree
void Btree::display(node* current)
{
if (current == NULL)
return;
queue<node*> q;
q.push(current);
while (!q.empty()) {
int l;
l = q.size();
for (int i = 0; i < l; i++) {
node* tNode = q.front();
q.pop();
for (int j = 0; j < tNode->size; j++)
if (tNode != NULL)
cout << tNode->key[j] << " ";
for (int j = 0; j < tNode->size + 1; j++)
if (tNode->ptr[j] != NULL)
q.push(tNode->ptr[j]);
cout << "\t";
}
cout << endl;
}
}
node* Btree::findParent(node* current, node* child)
{
node* parent;
if (current->isLeaf || (current->ptr[0])->isLeaf)
return NULL;
for (int i = 0; i < current->size + 1; i++) {
if (current->ptr[i] == child) {
parent = current;
return parent;
}
else {
parent = findParent(current->ptr[i], child);
if (parent != NULL)
return parent;
}
}
return parent;
}
signed main()
{
ios_base::sync_with_stdio(false);
Btree node;
cout << "The size of bucket is " << bucketSize << "! "
<< endl;
node.insert(1);
node.insert(2);
node.insert(3);
node.display(node.getRoot());
node.insert(4);
node.insert(5);
node.display(node.getRoot());
return 0;
}
import java.util.LinkedList;
import java.util.Queue;
// Node class represents a node in the B-tree
class Node {
boolean isLeaf; // Flag to check if the node is a leaf
Node[] ptr; // Array of child pointers
int[] key; // Array of keys
int size; // Current number of keys in the node
Node() {
key = new int[BTree.bucketSize];
ptr = new Node[BTree.bucketSize + 1];
}
}
// BTree class represents the B-tree structure
class BTree {
static int bucketSize = 3; // Size of the bucket or order of the B-tree
Node root; // Root of the B-tree
BTree() {
root = null; // Initialize the B-tree with no root initially
}
// Method to perform deletion in the B-tree (not implemented)
void deleteNode(int x) {
// Implement deletion logic if needed
}
// Method to search for a key in the B-tree
int search(int x) {
if (root == null)
return -1;
else {
Node current = root;
while (!current.isLeaf) {
for (int i = 0; i < current.size; i++) {
if (x < current.key[i]) {
current = current.ptr[i];
break;
}
if (i == current.size - 1) {
current = current.ptr[i + 1];
break;
}
}
}
for (int i = 0; i < current.size; i++) {
if (current.key[i] == x) {
// System.out.println("Key found ");
return 1;
}
}
// System.out.println("Key not found");
return 0;
}
}
// Method to display the B-tree level by level using a queue
void display(Node current) {
if (current == null)
return;
Queue<Node> queue = new LinkedList<>();
queue.add(current);
while (!queue.isEmpty()) {
int l = queue.size();
for (int i = 0; i < l; i++) {
Node tNode = queue.poll();
if (tNode != null) {
for (int j = 0; j < tNode.size; j++)
System.out.print(tNode.key[j] + " ");
for (int j = 0; j < tNode.size + 1; j++)
if (tNode.ptr[j] != null)
queue.add(tNode.ptr[j]);
System.out.print("\t");
}
}
System.out.println();
}
}
// Method to find the parent of a given node in the B-tree
Node findParent(Node current, Node child) {
Node parent = null;
if (current.isLeaf || current.ptr[0].isLeaf)
return null;
for (int i = 0; i < current.size + 1; i++) {
if (current.ptr[i] == child) {
parent = current;
return parent;
} else {
parent = findParent(current.ptr[i], child);
if (parent != null)
return parent;
}
}
return parent;
}
// Method to insert a key into the B-tree
void insert(int x) {
if (root == null) {
root = new Node();
root.key[0] = x;
root.isLeaf = true;
root.size = 1;
} else {
Node current = root;
Node parent = null;
while (!current.isLeaf) {
parent = current;
for (int i = 0; i < current.size; i++) {
if (x < current.key[i]) {
current = current.ptr[i];
break;
}
if (i == current.size - 1) {
current = current.ptr[i + 1];
break;
}
}
}
if (current.size < bucketSize) {
int i = 0;
while (i < current.size && x > current.key[i]) {
i++;
}
for (int j = current.size; j > i; j--) {
current.key[j] = current.key[j - 1];
}
current.key[i] = x;
current.size++;
current.ptr[current.size] = current.ptr[current.size - 1];
current.ptr[current.size - 1] = null;
} else {
Node newLeaf = new Node();
int[] tempNode = new int[bucketSize + 1];
for (int i = 0; i < bucketSize; i++) {
tempNode[i] = current.key[i];
}
int i = 0, j;
while (i < bucketSize && x > tempNode[i]) {
i++;
}
for (j = bucketSize; j > i; j--) {
tempNode[j] = tempNode[j - 1];
}
tempNode[i] = x;
newLeaf.isLeaf = true;
current.size = (bucketSize + 1) / 2;
newLeaf.size = (bucketSize + 1) - (bucketSize + 1) / 2;
current.ptr[current.size] = newLeaf;
newLeaf.ptr[newLeaf.size] = current.ptr[bucketSize];
current.ptr[newLeaf.size] = current.ptr[bucketSize];
current.ptr[bucketSize] = null;
for (i = 0; i < current.size; i++) {
current.key[i] = tempNode[i];
}
for (i = 0, j = current.size; i < newLeaf.size; i++, j++) {
newLeaf.key[i] = tempNode[j];
}
if (current == root) {
Node newRoot = new Node();
newRoot.key[0] = newLeaf.key[0];
newRoot.ptr[0] = current;
newRoot.ptr[1] = newLeaf;
newRoot.isLeaf = false;
newRoot.size = 1;
root = newRoot;
} else {
shiftLevel(newLeaf.key[0], findParent(root, current), newLeaf);
}
}
}
}
// Method to shift a level in the B-tree during insertion
void shiftLevel(int x, Node current, Node child) {
if (current.size < bucketSize) {
int i = 0;
while (x > current.key[i] && i < current.size)
i++;
for (int j = current.size; j > i; j--)
current.key[j] = current.key[j - 1];
for (int j = current.size + 1; j > i + 1; j--)
current.ptr[j] = current.ptr[j - 1];
current.key[i] = x;
current.size++;
current.ptr[i + 1] = child;
} else {
Node newInternal = new Node();
int[] tempKey = new int[bucketSize + 1];
Node[] tempPtr = new Node[bucketSize + 2];
for (int i = 0; i < bucketSize; i++)
tempKey[i] = current.key[i];
for (int i = 0; i < bucketSize + 1; i++)
tempPtr[i] = current.ptr[i];
int i = 0, j;
while (x > tempKey[i] && i < bucketSize)
i++;
for (j = bucketSize + 1; j > i; j--)
tempKey[j] = tempKey[j - 1];
tempKey[i] = x;
for (j = bucketSize + 2; j > i + 1; j--)
tempPtr[j] = tempPtr[j - 1];
tempPtr[i + 1] = child;
newInternal.isLeaf = false;
current.size = (bucketSize + 1) / 2;
newInternal.size = bucketSize - (bucketSize + 1) / 2;
for (i = 0, j = current.size + 1; i < newInternal.size; i++, j++)
newInternal.key[i] = tempKey[j];
for (i = 0, j = current.size + 1; i < newInternal.size + 1; i++, j++)
newInternal.ptr[i] = tempPtr[j];
if (current == root) {
Node newRoot = new Node();
newRoot.key[0] = current.key[current.size];
newRoot.ptr[0] = current;
newRoot.ptr[1] = newInternal;
newRoot.isLeaf = false;
newRoot.size = 1;
root = newRoot;
} else
shiftLevel(current.key[current.size], findParent(root, current), newInternal);
}
}
}
// Main class for testing the B-tree implementation
public class Main {
public static void main(String[] args) {
BTree bTree = new BTree();
System.out.println("The size of bucket is " + BTree.bucketSize + "! ");
// Insert some keys into the B-tree
bTree.insert(1);
bTree.insert(2);
bTree.insert(3);
bTree.display(bTree.root);
// Insert more keys and display the updated B-tree
bTree.insert(4);
bTree.insert(5);
bTree.display(bTree.root);
}
}
class Node:
def __init__(self):
self.is_leaf = False
self.ptr = [None] * (bucket_size + 1) # Pointers to child nodes
self.key = [None] * bucket_size # Keys stored in the node
self.size = 0 # Number of keys currently in the node
class BTree:
def __init__(self):
self.root = None # Root node of the B-tree
def get_root(self):
return self.root # Getter for the root node
def insert(self, x):
if self.root is None:
# B-tree is empty, create a new root
self.root = Node()
self.root.key[0] = x
self.root.is_leaf = True
self.root.size = 1
else:
current = self.root
parent = None
# Traverse the tree to find the appropriate leaf node for insertion
while not current.is_leaf:
parent = current
for i in range(current.size):
if current.key[i] is None or x < current.key[i]:
current = current.ptr[i]
break
if i == current.size - 1:
current = current.ptr[i + 1]
break
if current.size < bucket_size:
# Insert into a non-full leaf node
i = 0
while i < current.size and (current.key[i] is not None and x > current.key[i]):
i += 1
# Shift keys and pointers to make space for the new key
for j in range(current.size, i, -1):
current.key[j] = current.key[j - 1]
current.key[i] = x
current.size += 1
current.ptr[current.size] = current.ptr[current.size - 1]
current.ptr[current.size - 1] = None
else:
# Split the leaf node if it is full
new_leaf = Node()
temp_node = [None] * (bucket_size + 1)
# Copy keys to temporary array
for i in range(bucket_size):
temp_node[i] = current.key[i]
i = 0
while i < bucket_size and (temp_node[i] is not None and x > temp_node[i]):
i += 1
# Shift keys in the temporary array to make space for the new key
for j in range(bucket_size, i, -1):
temp_node[j] = temp_node[j - 1]
temp_node[i] = x
# Update sizes of the current and new_leaf nodes
new_leaf.is_leaf = True
current.size = (bucket_size + 1) // 2
new_leaf.size = bucket_size + 1 - (bucket_size + 1) // 2
# Update pointers
current.ptr[current.size] = new_leaf
new_leaf.ptr[new_leaf.size] = current.ptr[bucket_size]
current.ptr[new_leaf.size] = current.ptr[bucket_size]
current.ptr[bucket_size] = None
# Copy keys from the temporary array to the current and new_leaf nodes
for i in range(current.size):
current.key[i] = temp_node[i]
for i in range(current.size, bucket_size):
new_leaf.key[i - current.size] = temp_node[i]
if current == self.root:
# Update the root if splitting the root
new_root = Node()
new_root.key[0] = new_leaf.key[0]
new_root.ptr[0] = current
new_root.ptr[1] = new_leaf
new_root.is_leaf = False
new_root.size = 1
self.root = new_root
else:
# Propagate the split upwards
self.shift_level(new_leaf.key[0], parent, new_leaf)
def shift_level(self, x, current, child):
# Helper method to handle splitting of non-leaf nodes
if current.size < bucket_size:
i = 0
while i < current.size and (current.key[i] is not None and x > current.key[i]):
i += 1
# Shift keys and pointers to make space for the new key and child
for j in range(current.size, i, -1):
current.key[j] = current.key[j - 1]
for j in range(current.size + 1, i + 1, -1):
current.ptr[j] = current.ptr[j - 1]
current.key[i] = x
current.size += 1
current.ptr[i + 1] = child
else:
# Split the non-leaf node if it is full
new_internal = Node()
temp_key = [None] * (bucket_size + 1)
temp_ptr = [None] * (bucket_size + 2)
# Copy keys and pointers to temporary arrays
for i in range(bucket_size):
temp_key[i] = current.key[i]
for i in range(bucket_size + 1):
temp_ptr[i] = current.ptr[i]
i = 0
while i < bucket_size and (temp_key[i] is not None and x > temp_key[i]):
i += 1
# Shift keys in the temporary array to make space for the new key
for j in range(bucket_size, i, -1):
temp_key[j] = temp_key[j - 1]
temp_key[i] = x
# Shift pointers in the temporary array to make space for the new child
for j in range(bucket_size + 1, i + 1, -1):
temp_ptr[j] = temp_ptr[j - 1]
temp_ptr[i + 1] = child
new_internal.is_leaf = False
current.size = (bucket_size + 1) // 2
new_internal.size = bucket_size - (bucket_size + 1) // 2
# Copy keys and pointers from the temporary arrays to the current and new_internal nodes
for i in range(current.size + 1, bucket_size + 1):
new_internal.key[i - current.size - 1] = temp_key[i]
for i in range(current.size + 1, bucket_size + 2):
new_internal.ptr[i - current.size - 1] = temp_ptr[i]
if current == self.root:
# Update the root if splitting the root
new_root = Node()
new_root.key[0] = current.key[current.size]
new_root.ptr[0] = current
new_root.ptr[1] = new_internal
new_root.is_leaf = False
new_root.size = 1
self.root = new_root
else:
# Propagate the split upwards
self.shift_level(current.key[current.size], self.find_parent(self.root, current), new_internal)
def search(self, x):
# Search for a key in the B-tree
if self.root is None:
return -1 # B-tree is empty
else:
current = self.root
while not current.is_leaf:
for i in range(current.size):
if x < current.key[i]:
current = current.ptr[i]
break
if i == current.size - 1:
current = current.ptr[i + 1]
break
for i in range(current.size):
if current.key[i] == x:
return 1 # Key found
return 0 # Key not found
def display(self, current):
# Display the B-tree
if current is None:
return
q = [current]
while q:
l = len(q)
for _ in range(l):
t_node = q.pop(0)
for j in range(t_node.size):
if t_node.key[j] is not None:
print(t_node.key[j], end=' ')
for j in range(t_node.size + 1):
if t_node.ptr[j]:
q.append(t_node.ptr[j])
print('\t', end='')
print('\n')
def find_parent(self, current, child):
# Helper method to find the parent of a given node
parent = None
if current.is_leaf or current.ptr[0].is_leaf:
return None # No parent for leaf nodes
for i in range(current.size + 1):
if current.ptr[i] == child:
parent = current
return parent
else:
parent = self.find_parent(current.ptr[i], child)
if parent:
return parent
return parent
bucket_size = 3 # Set the bucket size for the B-tree
btree = BTree() # Create a new B-tree
print('The size of bucket is', bucket_size, '!')
# Insert elements into the B-tree
btree.insert(1)
btree.insert(2)
btree.insert(3)
btree.display(btree.get_root())
btree.insert(4)
btree.insert(5)
btree.display(btree.get_root())
class Node {
constructor() {
this.isLeaf = false;
this.ptr = new Array(bucketSize + 1).fill(null); // Pointers to child nodes
this.key = new Array(bucketSize); // Keys stored in the node
this.size = 0; // Number of keys currently in the node
}
}
class BTree {
constructor() {
this.root = null; // Root node of the B-tree
}
getRoot() {
return this.root; // Getter for the root node
}
insert(x) {
if (this.root === null) {
// B-tree is empty, create a new root
this.root = new Node();
this.root.key[0] = x;
this.root.isLeaf = true;
this.root.size = 1;
} else {
let current = this.root;
let parent;
// Traverse the tree to find the appropriate leaf node for insertion
while (current.isLeaf === false) {
parent = current;
for (let i = 0; i < current.size; i++) {
if (x < current.key[i]) {
current = current.ptr[i];
break;
}
if (i === current.size - 1) {
current = current.ptr[i + 1];
break;
}
}
}
if (current.size < bucketSize) {
// Insert into a non-full leaf node
let i = 0;
while (x > current.key[i] && i < current.size) {
i++;
}
// Shift keys and pointers to make space for the new key
for (let j = current.size; j > i; j--) {
current.key[j] = current.key[j - 1];
}
current.key[i] = x;
current.size++;
current.ptr[current.size] = current.ptr[current.size - 1];
current.ptr[current.size - 1] = null;
} else {
// Split the leaf node if it is full
let newLeaf = new Node();
let tempNode = new Array(bucketSize + 1);
// Copy keys to temporary array
for (let i = 0; i < bucketSize; i++) {
tempNode[i] = current.key[i];
}
let i = 0;
while (x > tempNode[i] && i < bucketSize) {
i++;
}
// Shift keys in the temporary array to make space for the new key
for (let j = bucketSize + 1; j > i; j--) {
tempNode[j] = tempNode[j - 1];
}
tempNode[i] = x;
// Update sizes of the current and newLeaf nodes
newLeaf.isLeaf = true;
current.size = Math.floor((bucketSize + 1) / 2);
newLeaf.size = bucketSize + 1 - Math.floor((bucketSize + 1) / 2);
// Update pointers
current.ptr[current.size] = newLeaf;
newLeaf.ptr[newLeaf.size] = current.ptr[bucketSize];
current.ptr[newLeaf.size] = current.ptr[bucketSize];
current.ptr[bucketSize] = null;
// Copy keys from the temporary array to the current and newLeaf nodes
for (let i = 0; i < current.size; i++) {
current.key[i] = tempNode[i];
}
for (let i = 0, j = current.size; i < newLeaf.size; i++, j++) {
newLeaf.key[i] = tempNode[j];
}
if (current === this.root) {
// Update the root if splitting the root
let newRoot = new Node();
newRoot.key[0] = newLeaf.key[0];
newRoot.ptr[0] = current;
newRoot.ptr[1] = newLeaf;
newRoot.isLeaf = false;
newRoot.size = 1;
this.root = newRoot;
} else {
// Propagate the split upwards
this.shiftLevel(newLeaf.key[0], parent, newLeaf);
}
}
}
}
shiftLevel(x, current, child) {
// Helper method to handle splitting of non-leaf nodes
if (current.size < bucketSize) {
let i = 0;
while (x > current.key[i] && i < current.size) {
i++;
}
// Shift keys and pointers to make space for the new key and child
for (let j = current.size; j > i; j--) {
current.key[j] = current.key[j - 1];
}
for (let j = current.size + 1; j > i + 1; j--) {
current.ptr[j] = current.ptr[j - 1];
}
current.key[i] = x;
current.size++;
current.ptr[i + 1] = child;
} else {
// Split the non-leaf node if it is full
let newInternal = new Node();
let tempKey = new Array(bucketSize + 1);
let tempPtr = new Array(bucketSize + 2);
// Copy keys and pointers to temporary arrays
for (let i = 0; i < bucketSize; i++) {
tempKey[i] = current.key[i];
}
for (let i = 0; i < bucketSize + 1; i++) {
tempPtr[i] = current.ptr[i];
}
let i = 0;
while (x > tempKey[i] && i < bucketSize) {
i++;
}
// Shift keys in the temporary array to make space for the new key
for (let j = bucketSize + 1; j > i; j--) {
tempKey[j] = tempKey[j - 1];
}
tempKey[i] = x;
// Shift pointers in the temporary array to make space for the new child
for (let j = bucketSize + 2; j > i + 1; j--) {
tempPtr[j] = tempPtr[j - 1];
}
tempPtr[i + 1] = child;
newInternal.isLeaf = false;
current.size = Math.floor((bucketSize + 1) / 2);
newInternal.size = bucketSize - Math.floor((bucketSize + 1) / 2);
// Copy keys and pointers from the temporary arrays to the current and newInternal nodes
for (let i = 0, j = current.size + 1; i < newInternal.size; i++, j++) {
newInternal.key[i] = tempKey[j];
}
for (let i = 0, j = current.size + 1; i < newInternal.size + 1; i++, j++) {
newInternal.ptr[i] = tempPtr[j];
}
if (current === this.root) {
// Update the root if splitting the root
let newRoot = new Node();
newRoot.key[0] = current.key[current.size];
newRoot.ptr[0] = current;
newRoot.ptr[1] = newInternal;
newRoot.isLeaf = false;
newRoot.size = 1;
this.root = newRoot;
} else {
// Propagate the split upwards
this.shiftLevel(current.key[current.size], this.findParent(this.root, current), newInternal);
}
}
}
search(x) {
// Search for a key in the B-tree
if (this.root === null) {
return -1; // B-tree is empty
} else {
let current = this.root;
while (current.isLeaf === false) {
for (let i = 0; i < current.size; i++) {
if (x < current.key[i]) {
current = current.ptr[i];
break;
}
if (i === current.size - 1) {
current = current.ptr[i + 1];
break;
}
}
}
for (let i = 0; i < current.size; i++) {
if (current.key[i] === x) {
return 1; // Key found
}
}
return 0; // Key not found
}
}
display(current) {
// Display the B-tree
if (current === null) {
return;
}
let q = [current];
while (q.length > 0) {
let l = q.length;
for (let i = 0; i < l; i++) {
let tNode = q.shift();
for (let j = 0; j < tNode.size; j++) {
if (tNode !== null) {
console.log(tNode.key[j] + ' ');
}
}
for (let j = 0; j < tNode.size + 1; j++) {
if (tNode.ptr[j] !== null) {
q.push(tNode.ptr[j]);
}
}
console.log('\t');
}
console.log('\n');
}
}
findParent(current, child) {
// Helper method to find the parent of a given node
let parent;
if (current.isLeaf || current.ptr[0].isLeaf) {
return null; // No parent for leaf nodes
}
for (let i = 0; i < current.size + 1; i++) {
if (current.ptr[i] === child) {
parent = current;
return parent;
} else {
parent = this.findParent(current.ptr[i], child);
if (parent !== null) {
return parent;
}
}
}
return parent;
}
}
const bucketSize = 3; // Set the bucket size for the B-tree
const btree = new BTree(); // Create a new B-tree
console.log('The size of bucket is ' + bucketSize + '!');
// Insert elements into the B-tree
btree.insert(1);
btree.insert(2);
btree.insert(3);
btree.display(btree.getRoot());
btree.insert(4);
btree.insert(5);
btree.display(btree.getRoot());
Output
The size of bucket is 3! 1 2 3 3 1 2 3 4 5
Time Complexity:
- Insertion: O(log (h*bucketSize)), where h is height of the tree, and bucketSize denotes the number of elements that can be stored in a single bucket.
- Deletion: O(log (h*bucketSize))
Auxiliary Space: O(n), n-> number of elements in the tree.