Statistics for Economics is a field that helps in the study, collection, analysis, interpretation, and organization of data for different ultimate objectives. Statistics help a user in gathering and analyzing huge numerical data easily and efficiently. For this, it provides various statistical tools and formulas that can be used to collect, interpret, and analyse the given set of data. Following are some of the important formulas (chapter-wise) used in Class 11th Statistics for Economics.
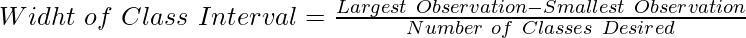
Where,
Largest Observation is the largest value of the given data set
Smallest Observation is the smallest value of thegiven data set
Number of Classes Desired is the number of class intervals required
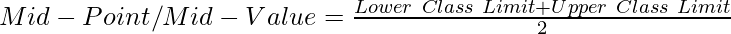
Where,
Lower Class Limit is the lower limit of a class interval of the given frequency distribution
Upper Class Limit is the upper limit of the same class interval of the given frequency distribution
3. Conversion of percentage into degrees in Pie Diagram
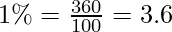
4. Adjustment Factor for any Class (Histogram)
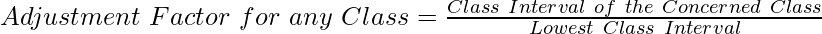
OR
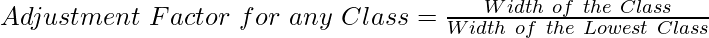
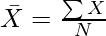
Where,
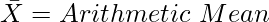
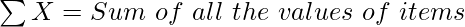
N = Total Number of Items
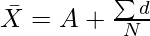
Where,
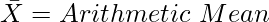
A = Assumed Mean
d = X – A (deviations of variables from assumed mean)
∑d = ∑(X – A) (sum of deviations of variables from assumed mean)
N = Total Number of Items
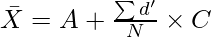
Where,
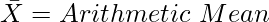
A = Assumed Mean
d = X – A (deviations of variables from assumed mean)
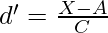 (Step Deviations; i.e., deviations divided by common factor)
(Step Deviations; i.e., deviations divided by common factor)
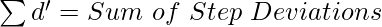
C = Common Factor
N = Total Number of Items
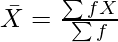
Where,
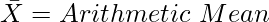
∑fX = Sum of the product of variables with the respective frequencies
∑f = Total Number of Items
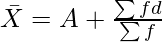
Where,
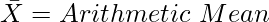
A = Assumed Mean
d = X – A (deviations of variables from assumed mean)
∑fd = Sum of the product of deviations (d) with the respective frequencies
∑f = Total Number of Items
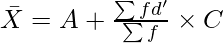
Where,
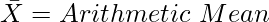
A = Assumed Mean
d = X – A (deviations of variables from assumed mean)
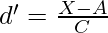 (Step Deviations; i.e., deviations divided by common factor)
(Step Deviations; i.e., deviations divided by common factor)
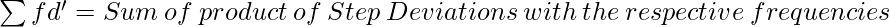
C = Common Factor
∑f = Total Number of Items
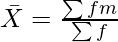
Where,
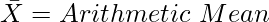
∑fm = Sum of the product of mid-points with the respective frequencies
∑f = Total Number of Items
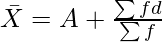
Where,
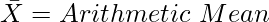
A = Assumed Mean
d = m – A (deviations of mid-points from assumed mean)
∑fd = Sum of the product of deviations (d) with the respective frequencies
∑f = Total Number of Items
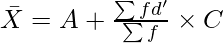
Where,
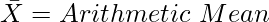
A = Assumed Mean
d = m – A (deviations of mid-points from assumed mean)
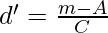 (Step Deviations; i.e., deviations divided by common factor)
(Step Deviations; i.e., deviations divided by common factor)
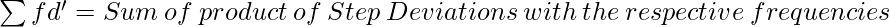
C = Common Factor
∑f = Total Number of Items
6. Charlier’s Accuracy Check
∑f(d + 1) = ∑fd + ∑f
Where,
f = Number of Observations
d = m – A (deviations of mid-points from assumed mean)
∑fd = Sum of the product of deviations (d) with the respective frequencies
∑f = Total Number of Items
- For Step Deviation Method
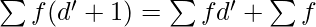
Where,
f = Number of Observations
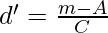 (Step Deviations; i.e., deviations divided by common factor)
(Step Deviations; i.e., deviations divided by common factor)
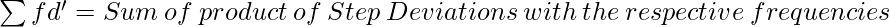
C = Common Factor
A = Assumed Mean
∑f = Total Number of Items
i) Individual Series:

Where,
X1, X2, ………………… Xn-1 = Given Values
Xn = Missing Value
ii) Discrete Series:
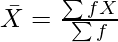
Where,
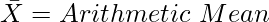
∑fX = Sum of the product of variables with the respective frequencies
∑f = Total Number of Items
iii) Continuous Series:
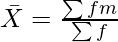
Where,
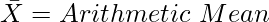
∑fm = Sum of the product of mid-points with the respective frequencies
∑f = Total Number of Items
8. Combined Mean
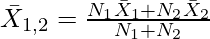
Where,
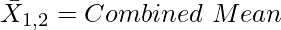
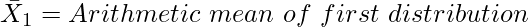
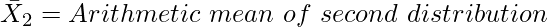
N1 = Number of Items of first distribution
N2 = Number of Items of second distribution
9. Corrected Mean
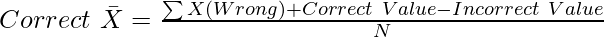
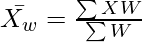
Where,
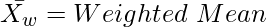
∑WX = Sum of product of items and respective weights
∑W = Sum of the weights
![Rendered by QuickLaTeX.com Median(M)=Size~of~[\frac{N+1}{2}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2245c6c1885bf461a7ad3cf64fdcd319_l3.png)
Where,
N = Number of Items
- If the Number of Items is Even
![Rendered by QuickLaTeX.com Median(M)=\frac{Size~of~[\frac{N}{2}]^{th}~item+Size~of~[\frac{N}{2}+1]^{th}~item}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3b38c9af31cd2355da66c9cf4d3a068b_l3.png)
Where,
N = Number of Items
![Rendered by QuickLaTeX.com Median(M)=Size~of~[\frac{N+1}{2}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2245c6c1885bf461a7ad3cf64fdcd319_l3.png)
Where,
N = Total of Frequency
Find out the value of ![Rendered by QuickLaTeX.com [\frac{N+1}{2}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7275d426c140eccda783171994189a18_l3.png) Locate the cumulative frequency which is equal to higher than
Locate the cumulative frequency which is equal to higher than ![Rendered by QuickLaTeX.com [\frac{N+1}{2}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7275d426c140eccda783171994189a18_l3.png) and then find the value corresponding to this cf. This value will be the Median value of the series.
and then find the value corresponding to this cf. This value will be the Median value of the series.
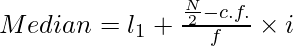
Where,
l1 = lower limit of the median class
c.f. = cumulative frequency of the class preceding the median class
f = simple frequency of the median class
i = class size of the median group or class
i) Individual Series:
![Rendered by QuickLaTeX.com Lower~Quartile(Q_1)=Size~of~[\frac{N+1}{4}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-68e112ce7a8d142ff924d707551fa523_l3.png)
![Rendered by QuickLaTeX.com Upper~Quartile(Q_3)=Size~of~3[\frac{N+1}{4}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-85b13c6a7d4e709203ca9352d9898132_l3.png)
Where,
N = Number of Items
ii) Discrete Series:
![Rendered by QuickLaTeX.com Lower~Quartile(Q_1)=Size~of~[\frac{N+1}{4}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-68e112ce7a8d142ff924d707551fa523_l3.png)
![Rendered by QuickLaTeX.com Upper~Quartile(Q_3)=Size~of~3[\frac{N+1}{4}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-85b13c6a7d4e709203ca9352d9898132_l3.png)
Where,
N = Cumulative Frequency
iii) Continuous Series:
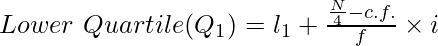
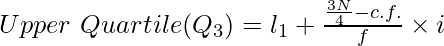
i) Individual Series:
![Rendered by QuickLaTeX.com D_{1}=[\frac{N+1}{10}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cfe1308fef4a30444ffd7b9438e5361a_l3.png)
![Rendered by QuickLaTeX.com D_{2}=[\frac{2(N+1)}{10}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6d919d93a44f7c1630b0d6fd4e8d62a7_l3.png)
……….![Rendered by QuickLaTeX.com D_{9}=[\frac{9(N+1)}{10}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2a92e53becd785e4fdeb80492c86903a_l3.png)
Where,
n is the total number of observations, D1 is First Decile, D2 is Second Decile,……….D9 is Ninth Decile.
ii) Discrete Series:
![Rendered by QuickLaTeX.com D_{1}=[\frac{N+1}{10}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cfe1308fef4a30444ffd7b9438e5361a_l3.png)
![Rendered by QuickLaTeX.com D_{2}=[\frac{2(N+1)}{10}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6d919d93a44f7c1630b0d6fd4e8d62a7_l3.png)
……….![Rendered by QuickLaTeX.com D_{9}=[\frac{9(N+1)}{10}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2a92e53becd785e4fdeb80492c86903a_l3.png)
Where,
n is the total number of observations (∑f), D1 is First Decile, D2 is Second Decile,……….D9 is Ninth Decile.
iii) Continuous Series:
![Rendered by QuickLaTeX.com D_{1}=[\frac{N}{10}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-168c4412885bcae85f231844e169afdd_l3.png)
![Rendered by QuickLaTeX.com D_{2}=[\frac{2N}{10}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ccd64c4d2d4835f3fcb0f054adf0ea8e_l3.png)
……….![Rendered by QuickLaTeX.com D_{9}=[\frac{9N}{10}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1453a2538af3b39d1daefd932dd6d3f7_l3.png)
Where,
n is the total number of observations (∑f), D1 is First Decile, D2 is Second Decile,……….D9 is Ninth Decile.
i) Individual Series:
![Rendered by QuickLaTeX.com P_{1}=[\frac{N+1}{100}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-79bc3449373a5bc37e14124d3edb0c15_l3.png)
![Rendered by QuickLaTeX.com P_{2}=[\frac{2(N+1)}{100}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-922358327c5ffbe356b6a2877f8f7fc1_l3.png)
![Rendered by QuickLaTeX.com P_{3}=[\frac{3(N+1)}{100}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1f11e7d9115a23a0ffb133a1b0dd2122_l3.png)
……….![Rendered by QuickLaTeX.com P_{99}=[\frac{99(N+1)}{100}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-48570243566f17d98e654dcf8af84a7a_l3.png)
Where,
n is the total number of observations (∑f), P1 is First Percentile, P2 is Second Percentile, P3 is Third Percentile, ……….P99 is Ninety Ninth Percentile.
ii) Discrete Series:
![Rendered by QuickLaTeX.com P_{1}=[\frac{N+1}{100}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-79bc3449373a5bc37e14124d3edb0c15_l3.png)
![Rendered by QuickLaTeX.com P_{2}=[\frac{2(N+1)}{100}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-922358327c5ffbe356b6a2877f8f7fc1_l3.png)
![Rendered by QuickLaTeX.com P_{3}=[\frac{3(N+1)}{100}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1f11e7d9115a23a0ffb133a1b0dd2122_l3.png)
……….![Rendered by QuickLaTeX.com P_{99}=[\frac{99(N+1)}{100}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-48570243566f17d98e654dcf8af84a7a_l3.png)
Where,
n is the total number of observations (∑f), P1 is First Percentile, P2 is Second Percentile, P3 is Third Percentile, ……….P99 is Ninety Ninth Percentile.
iii) Continuous Series:
![Rendered by QuickLaTeX.com P_{1}=[\frac{N}{100}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7a2b94425aea078e6aaf8fe77d746b57_l3.png)
![Rendered by QuickLaTeX.com P_{2}=[\frac{2N}{100}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-76eac6890aa265f405e242b957b5ede4_l3.png)
![Rendered by QuickLaTeX.com P_{3}=[\frac{3N}{100}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9f0f793adcf498b8b91f1fa2c6ea3574_l3.png)
……….![Rendered by QuickLaTeX.com P_{99}=[\frac{99N}{100}]^{th}~item](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-29b048d05e1aba525c1d518c29bf8550_l3.png)
Where,
n is the total number of observations (∑f), P1 is First Percentile, P2 is Second Percentile, P3 is Third Percentile, ……….P99 is Ninety Ninth Percentile.
Mode is the value that occurs the largest number of times.
In the case of regular and homogeneous frequencies, and single maximum frequency, Mode is the value corresponding to the highest frequency. Otherwise, the grouping method is used.
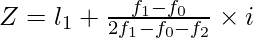
Where,
Z = Value of Mode
l1 = lower limit of the modal class
f1 = frequency of modal class
f0 = frequency of pre-modal class
f2 = frequency of the next higher class or post-modal class
i = size of the modal group
Mode = 3 Median – 2 Mean
Range(R) = Largest Item(L) – Smallest Item(S)
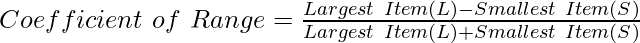
In Individual Series, the largest and smallest item is taken from the given observations.
In Discrete Series, the largest and smallest item is taken from the given frequencies.
In Continuous Series, the first method to calculate coefficient of range is to take the difference between the upper and lower limit of the highest and lowest class interval respectively. The second method is to take the difference between the mid-points of the highest class limit and lowest class limit.
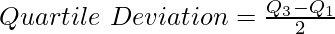
Where,
Q3 = Upper Quartile (Size of ![Rendered by QuickLaTeX.com 3[\frac{N+1}{4}]^{th}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3955e3de8e7c8b0a315e7614a30ec110_l3.png) item)
item)
Q1 = Lower Quartile (Size of ![Rendered by QuickLaTeX.com [\frac{N+1}{4}]^{th}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5839698023a23148c6db88a2cf1517c0_l3.png) item)
item)
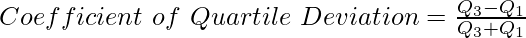
Where,
Q3 = Upper Quartile (Size of ![Rendered by QuickLaTeX.com 3[\frac{N+1}{4}]^{th}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3955e3de8e7c8b0a315e7614a30ec110_l3.png) item)
item)
Q1 = Lower Quartile (Size of ![Rendered by QuickLaTeX.com [\frac{N+1}{4}]^{th}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5839698023a23148c6db88a2cf1517c0_l3.png) item)
item)
i) Individual Series:
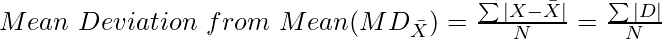
- Mean Deviation from Median
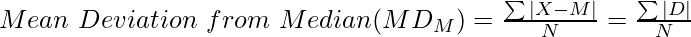
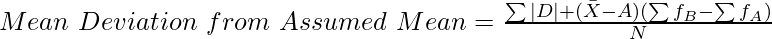
Where,
∑|D| = Sum of absolute deviations from Assumed Mean
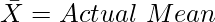
A = Assumed Mean
∑fB = Number of Values from actual mean
∑fA = Number of values below actual mean including actual mean
N = Number of Observations
ii) Discrete Series:
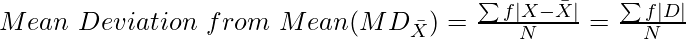
- Mean Deviation from Median
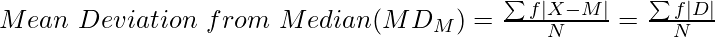
Where,
∑f|D| = Sum of product of frequency and absolute deviations from Assumed Mean
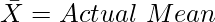
M = Median
N = Number of Observations
iii) Continuous Series:
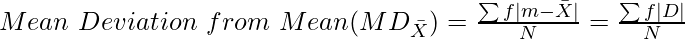
- Mean Deviation from Median
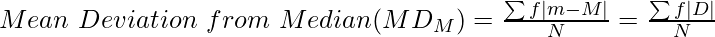
Where,
∑f|D| = Sum of product of frequency and absolute deviations from Assumed Mean
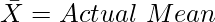
m = Mid-value
M = Median
N = Number of Observations
22. Coefficient of Mean Deviation
- Coefficient of Mean Deviation from Mean
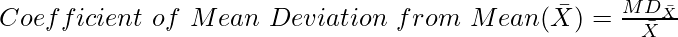
Where,
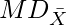 = Mean Deviation from Mean
= Mean Deviation from Mean
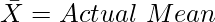
- Coefficient of Mean Deviation from Median
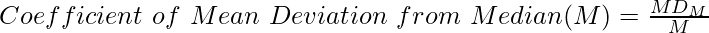
Where,
MDM = Mean Deviation from Median
M = Median
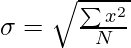
Where,
σ = Standard Deviation
∑x2 = Sum total of the squares of deviations from the actual mean
N = Number of pairs of observations
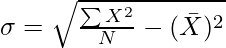
Or
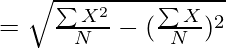
Where,
σ = Standard Deviation
∑X2 = Sum total of the squares of observations
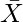 = Actual Mean
= Actual Mean
N = Number of Observations
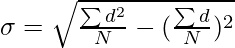
Where,
σ = Standard Deviation
∑d = Sum total of deviations from assumed mean
∑d2 = Sum total of squares of deviations
N = Number of pairs of observations
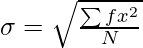
Where,
σ = Standard Deviation
∑fx2 = Sum total of the squared deviations multiplied by frequency
N = Number of pairs of observations
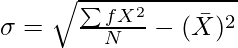
Or
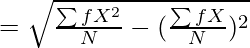
Where,
σ = Standard Deviation
∑fx2 = Sum total of the squared deviations multiplied by frequency
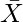 = Actual Mean
= Actual Mean
N = Number of Observations
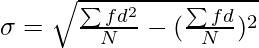
Or
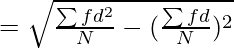
Where,
σ = Standard Deviation
∑fd = Sum total of deviations multiplied by frequencies
∑d2 = Sum total of the squared deviations multiplied by frequencies
N = Number of pairs of observations
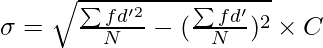
Where,
σ = Standard Deviation
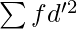 = Sum total of the squared step deviations multiplied by frequencies
= Sum total of the squared step deviations multiplied by frequencies
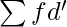 = Sum total of step deviations multiplied by frequencies
= Sum total of step deviations multiplied by frequencies
N = Number of pairs of observations
σ = 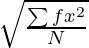
OR
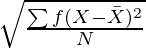
Where,
σ = Standard Deviation
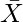 = Actual Mean
= Actual Mean
∑fx2 = Sum total of the deviations of every mid-value of the class intervals multiplied by frequency
N = Number of pair of observations
σ = 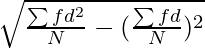
Where,
σ = Standard Deviation
∑fd2 = Sum total of the squared deviations multiplied by frequency
∑fd = Sum total of deviations multiplied by frequency
N = Number of pair of observations
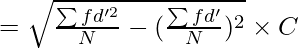
Where,
σ = Standard Deviation
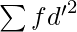 = Sum total of the squared step deviations multiplied by frequency
= Sum total of the squared step deviations multiplied by frequency
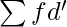 = Sum total of step deviations multiplied by frequency
= Sum total of step deviations multiplied by frequency
C = Common Factor
N = Number of pair of observations
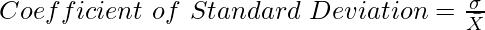
Where,
σ = Standard Deviation
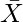 = Arithmetic Mean
= Arithmetic Mean
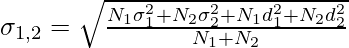
Where,
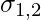 = Combined Standard Deviation of two groups
= Combined Standard Deviation of two groups
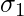 =Standard Deviation of first group
=Standard Deviation of first group
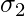 = Standard Deviation of second group
= Standard Deviation of second group
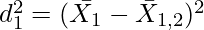
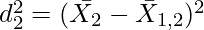
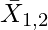 = Combined Arithmetic Mean of two groups
= Combined Arithmetic Mean of two groups
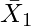 = Arithmetic Mean of first group
= Arithmetic Mean of first group
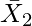 = Arithmetic Mean of second group
= Arithmetic Mean of second group
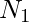 = Number of Observations in the first group
= Number of Observations in the first group
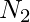 = Number of Observations in the second group
= Number of Observations in the second group
Variance = σ2
Where,
σ = Standard Deviation
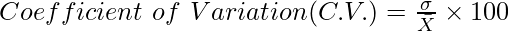
Where,
C.V. = Coefficient of Variation
σ = Standard Deviation
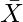 = Arithmetic Mean
= Arithmetic Mean
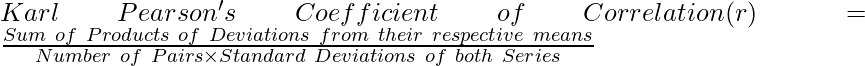
Or, 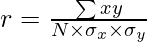
Or, 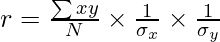
Or, 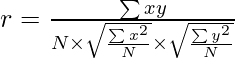
Or, 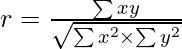
Where,
N = Number of Pair of Observations
x = Deviation of X series from Mean 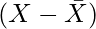
y = Deviation of Y series from Mean 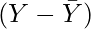
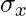 = Standard Deviation of X series
= Standard Deviation of X series
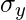 = Standard Deviation of Y series
= Standard Deviation of Y series
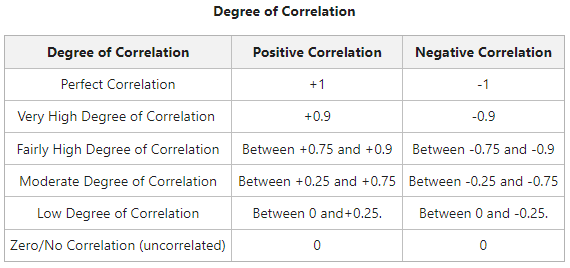
r = Coefficient of Correlation
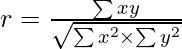
Where,
∑xy = Sum of Product of Deviation of X series and Y series from their respective Means
∑x2 = Sum of squares of Deviation of X Series
∑y2 = Sum of squares of Deviation of Y Series
r = Coefficient of Correlation
N = Number of Pair of Observations
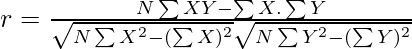
Where,
∑XY = Sum of Product of X Series and Y Series
∑X = Sum of Series X
∑Y = Sum of Series Y
∑X2 = Sum of squares of Series X
∑Y2 = Sum of squares of Series Y
r = Coefficient of Correlation
N = Number of Pair of Observations
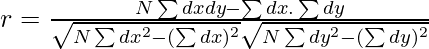
Where,
N = Number of pair of observations
∑dx = Sum of deviations of X values from assumed mean
∑dy = Sum of deviations of Y values from assumed mean
∑dx2 = Sum of squared deviations of X values from assumed mean
∑dy2 = Sum of squared deviations of Y values from assumed mean
∑dxdy = Sum of the products of deviations dx and dy
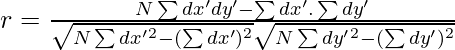
Where,
N = Number of pair of observations
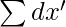 = Sum of deviations of X values from assumed mean
= Sum of deviations of X values from assumed mean
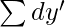 = Sum of deviations of Y values from assumed mean
= Sum of deviations of Y values from assumed mean
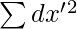 = Sum of squared deviations of X values from assumed mean
= Sum of squared deviations of X values from assumed mean
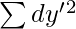 = Sum of squared deviations of Y values from assumed mean
= Sum of squared deviations of Y values from assumed mean
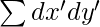 = Sum of the products of deviations
= Sum of the products of deviations 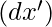 and
and 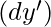
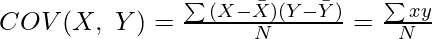
Where,
COV(X,Y) = Covariance of X and Y
∑xy = Sum of Product of Deviation of X series and Y series from their respective Means
N = Number of pair of observations
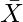 = Arithmetic Mean of Series X
= Arithmetic Mean of Series X
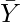 = Arithmetic Mean of Series Y
= Arithmetic Mean of Series Y
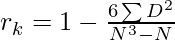
Where,
rk = Coefficient of rank correlation
D = Rank differences
N = Number of variables
![Rendered by QuickLaTeX.com r_k=1-\frac{6[\sum D^2+\frac{1}{12}(m_1^3-m_1)+\frac{1}{12}(m_2^3-m_2)+...]}{N^3-N}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1c4a6e4f166c2e117f1dd90a784cb433_l3.png)
Here,
m1, m2, ……. are the number of times a value has repeated in the given X, Y, …….. series respectively.
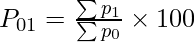
Where,
P01 = Index Number of the Current Year
∑p1 = Total of the current year’s price of all commodities
∑p0 = Total of the base year’s price of all commodities
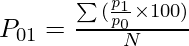
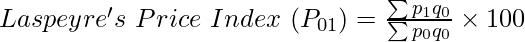
Here,
P01 = Price Index of the current year
p0 = Price of goods at base year
q0 = Quantity of goods at base year
p1 = Price of goods at the current year
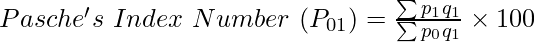
Here,
P01 = Price Index of the current year
p0 = Price of goods in the base year
q1 = Quantity of goods in the base year
p1 = Price of goods in the current year
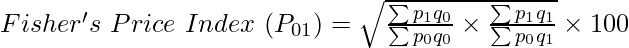
Here,
P01 = Price Index of the current year
p0 = Price of goods in the base year
q1 = Quantity of goods in the base year
p1 = Price of goods in the current year
Fisher’s Method is considered the Ideal Method for Constructing Index Numbers.
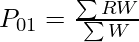
Where,
∑RW = Sum of product of Price Relatives (R) and Value Weights (W)
∑W = Sum of Value Weights
- Aggregate Expenditure Method
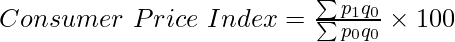
Where,
p1 = Price of goods in the current year
p0 = Price of goods in the base year
q0 = Quantity of goods at base year
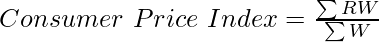
Where,
∑RW = Sum of product of Price Relatives (R) and Value Weights (W)
∑W = Sum of Value Weights
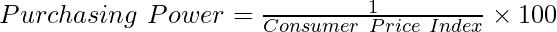
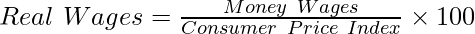
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...