Skip to content
Related Articles
Get the best out of our app
GeeksforGeeks App
Open App
geeksforgeeks
Browser
Continue

Related Articles

Implicit differentiation – Advanced Examples

Improve Article
Save Article
Like Article
author
rathoreatul27
contributor
9 published articles
Improve Article
Save Article
Like Article

In the previous article, we have discussed the introduction part and some basic examples of Implicit differentiation. So in this article, we will discuss some advanced examples of implicit differentiation.

Implicit Differentiation

Implicit differentiation is a method that makes use of the chain rule to differentiate implicitly defined functions. It is generally not easy to find the function explicitly and then differentiate. Instead, we can totally differentiate f(x, y) and then solve the rest of the equation to find the value of 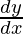\frac{dy}{dx}. Even when it is possible to explicitly solve the original equation, the formula resulting from total differentiation is, in general, much simpler and easier to use.

Method to solve

  • Differentiate both sides of the equation with respect to x.
  • Follow the rules of differentiation.
  • Use the chain rule to differentiate expressions involving y.
  • Solve the equation for \frac{dy}{dx}

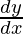
Advanced Examples 

Example 1: Find the derivative of y = cos(5x – 3y)?

Solution:

Given equation:

                      y = cos(5x – 3y)

Step 1: Differentiating both sides wrt x,

                     \frac{d}{dx}y = \frac{d}{dx}(cos(5x - 3y))

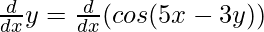
Step 2: Using Chain Rule

                    \frac{dy}{dx} = -sin(5x-3y)\frac{d}{dx}(5x - 3y) \\ \\ \qquad \qquad \ \ \frac{dy}{dx} = -sin(5x-3y)(5 - 3\frac{dy}{dx})

Step 3: Expanding the above equation

                     \frac{dy}{dx} = -5sin(5x-3y)+ 3sin(5x-3y)\frac{dy}{dx}

Step 4: Taking all terms with dy/dx on LHS

                    \frac{dy}{dx} - 3sin(5x-3y)\frac{dy}{dx}= -5sin(5x-3y)

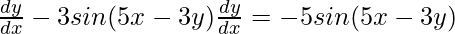
Step 5: Taking dy/dx common from the LHS of equation

                    \frac{dy}{dx}(1 - 3sin(5x-3y))= -5sin(5x-3y)

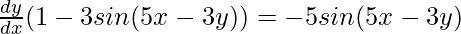
Step 6: Isolate dy/dx

                    \frac{dy}{dx}= \frac{-5sin(5x-3y)}{1 - 3sin(5x-3y)}

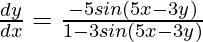
Example 2: Find the derivative of (x² + y²)³ = 5x²y²?

Solution:

Given equation:

(x² + y²)³ = 5x²y²

Differentiating both sides:

\begin{aligned} \frac{d}{dx}(x^2+y^2)^3 &=\frac{d}{dx}5x^2y^2 \\ 3(x^2+y^2)^2\frac{d}{dx}(x^2+y^2) &=5\frac{d}{dx}x^2y^2 \\ 3(x^2+y^2)^2(2x+2y\frac{dy}{dx}) &=5(2xy^2+2y\frac{dy}{dx}x^2) \\ 6x(x^2+y^2)^2+6y(x^2+y^2)^2\frac{dy}{dx} &=10xy^2+10x^2y\frac{dy}{dx} \\ 6y(x^2+y^2)^2\frac{dy}{dx}-10x^2y\frac{dy}{dx} &=10xy^2-6x(x^2+y^2)^2 \\ (6y(x^2+y^2)^2-10x^2y)\frac{dy}{dx} &=10xy^2-6x(x^2+y^2)^2 \\ \frac{dy}{dx} &=\frac{10xy^2-6x(x^2+y^2)^2}{6y(x^2+y^2)^2-10x^2y} \\ \end{aligned}

Example 3: Find the derivative of 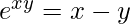 e^{xy²} = x-y?

Solution:

Given equation:

e^{xy²} = x-y

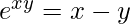
Differentiating both sides:

\begin{aligned} \frac{d}{dx}e^{xy²}&=\frac{d}{dx}(x-y) \\ e^{xy²}\frac{d}{dx}(xy²)&=1-\frac{dy}{dx} \\ e^{xy²}(y^2+x.2y\frac{dy}{dx})&=1-\frac{dy}{dx} \\ y^2e^{xy²}+2xye^{xy²}\frac{dy}{dx}&=1-\frac{dy}{dx} \\ e^{xy²}2xy\frac{dy}{dx}+\frac{dy}{dx}&=1-y^2e^{xy²} \\ (2xye^{xy²}+1)\frac{dy}{dx}&=1-y^2e^{xy²} \\ \frac{dy}{dx}&=\frac{1-y^2e^{xy²}}{2xye^{xy²}+1} \\ \frac{dy}{dx}&=\frac{1-y^2(x-y)}{2xy(x-y)+1} \\ \frac{dy}{dx}&=\frac{1-xy^2+y^3}{2x^2y-2xy^2+1} \\ \end{aligned}

Example 4: Find the derivative of y = ln(x)?

Solution:

Given equation:

y = ln(x)

=> ey = x

Differentiating both sides:

\begin{aligned} \frac{d}{dx}e^{y}&=\frac{d}{dx}(x) \\ e^{y}\frac{dy}{dx}&=1 \\ \frac{dy}{dx}&=\frac{1}{e^y} \\ \frac{dy}{dx}&=\frac{1}{x} \\ \end{aligned}


My Personal Notes arrow_drop_up
Last Updated : 28 Jan, 2021
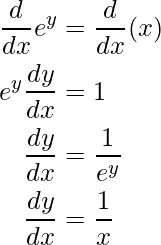
Like Article
Save Article
Similar Reads
1. Implicit Differentiation
2. Proofs for the derivatives of eˣ and ln(x) - Advanced differentiation
3. Disguised Derivatives - Advanced differentiation | Class 12 Maths
4. Advanced Differentiation
5. Derivatives of Implicit Functions - Continuity and Differentiability | Class 12 Maths
6. Logarithmic Differentiation
7. Differentiation of Inverse Trigonometric Functions
8. Class 12 RD Sharma Solutions - Chapter 11 Differentiation - Exercise 11.6
9. Class 12 RD Sharma Solutions- Chapter 11 Differentiation - Exercise 11.8 | Set 1
10. Class 12 RD Sharma Solutions- Chapter 11 Differentiation - Exercise 11.8 | Set 2
Related Tutorials
1. Linear Algebra
2. Maths
3. Physics
4. Chemistry
5. CBSE Class 12 Syllabus 2023-2024
Previous
Implicit Differentiation
Next
Advanced Differentiation
Article Contributed By :
https://media.geeksforgeeks.org/auth/avatar.png
rathoreatul27
rathoreatul27
Vote for difficulty
Article Tags :
Report Issue
We use cookies to ensure you have the best browsing experience on our website. By using our site, you acknowledge that you have read and understood our Cookie Policy & Privacy Policy
Lightbox