Implementation of Perceptron Algorithm for XNOR Logic Gate with 2-bit Binary Input

Last Updated : 13 Jul, 2020

In the field of Machine Learning, the Perceptron is a Supervised Learning Algorithm for binary classifiers. The Perceptron Model implements the following function:

$\begin{array}{c} \hat{y}=\Theta\left(w_{1} x_{1}+w_{2} x_{2}+\ldots+w_{n} x_{n}+b\right) \\ =\Theta(\mathbf{w} \cdot \mathbf{x}+b) \\ \text { where } \Theta(v)=\left\{\begin{array}{cc} 1 & \text { if } v \geqslant 0 \\ 0 & \text { otherwise } \end{array}\right. \end{array}$

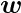
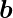
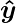
For a particular choice of the weight vector $\boldsymbol{w}$ and bias parameter $\boldsymbol{b}$ , the model predicts output $\boldsymbol{\hat{y}}$ for the corresponding input vector $\boldsymbol{x}$ .

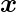
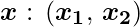
XNOR logical function truth table for 2-bit binary variables, i.e, the input vector $\boldsymbol{x} : (\boldsymbol{x_{1}}, \boldsymbol{x_{2}})$ and the corresponding output $\boldsymbol{y}$ –

$\boldsymbol{x_{1}}$	$\boldsymbol{x_{2}}$	$\boldsymbol{y}$
0	0	1
0	1	0
1	0	0
1	1	1

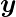
We can observe that, 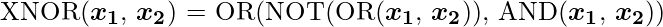$XNOR(\boldsymbol{x_{1}}, \boldsymbol{x_{2}}) = OR(NOT(OR(\boldsymbol{x_{1}}, \boldsymbol{x_{2}})), AND(\boldsymbol{x_{1}}, \boldsymbol{x_{2}}))$
Designing the Perceptron Network:

Step1: Now for the corresponding weight vector 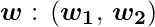$\boldsymbol{w} : (\boldsymbol{w_{1}}, \boldsymbol{w_{2}})$ of the input vector 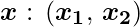$\boldsymbol{x} : (\boldsymbol{x_{1}}, \boldsymbol{x_{2}})$ to the OR and AND node, the associated Perceptron Function can be defined as:
$\boldsymbol{\hat{y}_{1}} = \Theta\left(w_{1} x_{1}+w_{2} x_{2}+b_{OR}\right)$
$\boldsymbol{\hat{y}_{2}} = \Theta\left(w_{1} x_{1}+w_{2} x_{2}+b_{AND}\right)$
Step2: The output 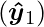$($\boldsymbol{\hat{y}}_{1}$)$ from the OR node will be inputed to the NOT node with weight 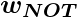$\boldsymbol{w_{NOT}}$ and the associated Perceptron Function can be defined as:
$\boldsymbol{\hat{y}_{3}} = \Theta\left(w_{NOT} \boldsymbol{\hat{y}_{1}}+b_{NOT}\right)$
Step3: The output 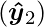$($\boldsymbol{\hat{y}}_{2}$)$ from the AND node and the output 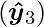$($\boldsymbol{\hat{y}}_{3}$)$ from NOT node as mentioned in Step2 will be inputed to the OR node with weight 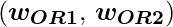$(\boldsymbol{w_{OR1}}, \boldsymbol{w_{OR2}})$ . Then the corresponding output 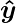$\boldsymbol{\hat{y}}$ is the final output of the XNOR logic function. The associated Perceptron Function can be defined as:
$\boldsymbol{\hat{y}} = \Theta\left(w_{OR1} \boldsymbol{\hat{y}_{3}}+w_{OR2} \boldsymbol{\hat{y}_{2}}+b_{OR}\right)$

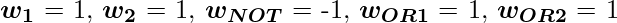For the implementation, the weight parameters are considered to be $\boldsymbol{w_{1}} = 1, \boldsymbol{w_{2}} = 1, \boldsymbol{w_{NOT}} = -1, \boldsymbol{w_{OR1}} = 1, \boldsymbol{w_{OR2}} = 1$ and the bias parameters are $\boldsymbol{b_{AND}} = -1.5, \boldsymbol{b_{OR}} = -0.5, \boldsymbol{b_{NOT}} = 0.5$ .

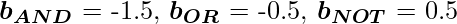Python Implementation:

# importing Python library
import numpy as np
  
# define Unit Step Function
def unitStep(v):
    if v >= 0:
        return 1
    else:
        return 0
  
# design Perceptron Model
def perceptronModel(x, w, b):
    v = np.dot(w, x) + b
    y = unitStep(v)
    return y
  
# NOT Logic Function
# wNOT = -1, bNOT = 0.5
def NOT_logicFunction(x):
    wNOT = -1
    bNOT = 0.5
    return perceptronModel(x, wNOT, bNOT)
  
# AND Logic Function
# w1 = 1, w2 = 1, bAND = -1.5
def AND_logicFunction(x):
    w = np.array([1, 1])
    bAND = -1.5
    return perceptronModel(x, w, bAND)
  
# OR Logic Function
# here w1 = wOR1 = 1, 
# w2 = wOR2 = 1, bOR = -0.5
def OR_logicFunction(x):
    w = np.array([1, 1])
    bOR = -0.5
    return perceptronModel(x, w, bOR)
  
# XNOR Logic Function
# with AND, OR and NOT  
# function calls in sequence
def XNOR_logicFunction(x):
    y1 = OR_logicFunction(x)
    y2 = AND_logicFunction(x)
    y3 = NOT_logicFunction(y1)
    final_x = np.array([y2, y3])
    finalOutput = OR_logicFunction(final_x)
    return finalOutput
  
# testing the Perceptron Model
test1 = np.array([0, 1])
test2 = np.array([1, 1])
test3 = np.array([0, 0])
test4 = np.array([1, 0])
  
print("XNOR({}, {}) = {}".format(0, 1, XNOR_logicFunction(test1)))
print("XNOR({}, {}) = {}".format(1, 1, XNOR_logicFunction(test2)))
print("XNOR({}, {}) = {}".format(0, 0, XNOR_logicFunction(test3)))
print("XNOR({}, {}) = {}".format(1, 0, XNOR_logicFunction(test4)))

Output:

XNOR(0, 1) = 0
XNOR(1, 1) = 1
XNOR(0, 0) = 1
XNOR(1, 0) = 0

Here, the model predicted output (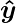 $\boldsymbol{\hat{y}}$ ) for each of the test inputs are exactly matched with the XNOR logic gate conventional output ( 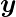$\boldsymbol{y}$ ) according to the truth table.
Hence, it is verified that the perceptron algorithm for XNOR logic gate is correctly implemented.

My Personal Notes

Related Articles