Implementation of Perceptron Algorithm for NAND Logic Gate with 2-bit Binary Input

In the field of Machine Learning, the Perceptron is a Supervised Learning Algorithm for binary classifiers. The Perceptron Model implements the following function:

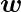
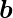
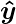
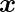
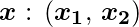
For a particular choice of the weight vector and bias parameter , the model predicts output for the corresponding input vector . NAND logical function truth table for 2-bit binary variables, i.e, the input vector and the corresponding output –

0	0	1
0	1	1
1	0	1
1	1	0

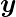
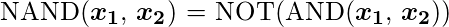
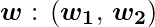
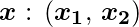
We can observe that, Now for the corresponding weight vector of the input vector to the AND node, the associated Perceptron Function can be defined as:

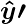
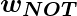
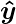
Later on, the output of AND node is the input to the NOT node with weight . Then the corresponding output is the final output of the NAND logic function and the associated Perceptron Function can be defined as:

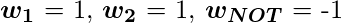
For the implementation, considered weight parameters are and the bias parameters are . Python Implementation:

# importing Python library
import numpy as np

# define Unit Step Function
def unitStep(v):
    if v >= 0:
        return 1
    else:
        return 0

# design Perceptron Model
def perceptronModel(x, w, b):
    v = np.dot(w, x) + b
    y = unitStep(v)
    return y

# NOT Logic Function
# wNOT = -1, bNOT = 0.5
def NOT_logicFunction(x):
    wNOT = -1
    bNOT = 0.5
    return perceptronModel(x, wNOT, bNOT)

# AND Logic Function
# w1 = 1, w2 = 1, bAND = -1.5
def AND_logicFunction(x):
    w = np.array([1, 1])
    bAND = -1.5
    return perceptronModel(x, w, bAND)

# NAND Logic Function
# with AND and NOT
# function calls in sequence
def NAND_logicFunction(x):
    output_AND = AND_logicFunction(x)
    output_NOT = NOT_logicFunction(output_AND)
    return output_NOT

# testing the Perceptron Model
test1 = np.array([0, 1])
test2 = np.array([1, 1])
test3 = np.array([0, 0])
test4 = np.array([1, 0])

print("NAND({}, {}) = {}".format(0, 1, NAND_logicFunction(test1)))
print("NAND({}, {}) = {}".format(1, 1, NAND_logicFunction(test2)))
print("NAND({}, {}) = {}".format(0, 0, NAND_logicFunction(test3)))
print("NAND({}, {}) = {}".format(1, 0, NAND_logicFunction(test4)))

Output:

NAND(0, 1) = 1
NAND(1, 1) = 0
NAND(0, 0) = 1
NAND(1, 0) = 1

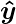
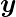
Here, the model predicted output () for each of the test inputs are exactly matched with the NAND logic gate conventional output () according to the truth table for 2-bit binary input. Hence, it is verified that the perceptron algorithm for NAND logic gate is correctly implemented.