Implementation of DFS using adjacency matrix
Last Updated :
20 Mar, 2023
Depth First Search (DFS) has been discussed in this article which uses adjacency list for the graph representation. In this article, adjacency matrix will be used to represent the graph.
Adjacency matrix representation: In adjacency matrix representation of a graph, the matrix mat[][] of size n*n (where n is the number of vertices) will represent the edges of the graph where mat[i][j] = 1 represents that there is an edge between the vertices i and j while mat[i][j] = 0 represents that there is no edge between the vertices i and j.
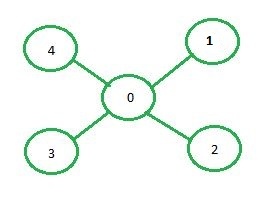
Below is the adjacency matrix representation of the graph shown in the above image:
0 1 2 3 4
0 0 1 1 1 1
1 1 0 0 0 0
2 1 0 0 0 0
3 1 0 0 0 0
4 1 0 0 0 0
Examples:
Input: source = 0
Output: 0 1 3 2
Input: source = 0

Output: 0 1 2 3 4
Approach:
- Create a matrix of size n*n where every element is 0 representing there is no edge in the graph.
- Now, for every edge of the graph between the vertices i and j set mat[i][j] = 1.
- After the adjacency matrix has been created and filled, call the recursive function for the source i.e. vertex 0 that will recursively call the same function for all the vertices adjacent to it.
- Also, keep an array to keep track of the visited vertices i.e. visited[i] = true represents that vertex i has been visited before and the DFS function for some already visited node need not be called.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
vector<vector<int> > adj;
void addEdge(int x, int y)
{
adj[x][y] = 1;
adj[y][x] = 1;
}
void dfs(int start, vector<bool>& visited)
{
cout << start << " ";
visited[start] = true;
for (int i = 0; i < adj[start].size(); i++) {
if (adj[start][i] == 1 && (!visited[i])) {
dfs(i, visited);
}
}
}
int main()
{
int v = 5;
int e = 4;
adj = vector<vector<int> >(v, vector<int>(v, 0));
addEdge(0, 1);
addEdge(0, 2);
addEdge(0, 3);
addEdge(0, 4);
vector<bool> visited(v, false);
dfs(0, visited);
}
|
Java
import java.io.*;
class GFG {
static int[][] adj;
static void addEdge(int x, int y)
{
adj[x][y] = 1;
adj[y][x] = 1;
}
static void dfs(int start, boolean[] visited)
{
System.out.print(start + " ");
visited[start] = true;
for (int i = 0; i < adj[start].length; i++) {
if (adj[start][i] == 1 && (!visited[i])) {
dfs(i, visited);
}
}
}
public static void main(String[] args)
{
int v = 5;
int e = 4;
adj = new int[v][v];
addEdge(0, 1);
addEdge(0, 2);
addEdge(0, 3);
addEdge(0, 4);
boolean[] visited = new boolean[v];
dfs(0, visited);
}
}
|
Python3
class Graph:
adj = []
def __init__(self, v, e):
self.v = v
self.e = e
Graph.adj = [[0 for i in range(v)]
for j in range(v)]
def addEdge(self, start, e):
Graph.adj[start][e] = 1
Graph.adj[e][start] = 1
def DFS(self, start, visited):
print(start, end = ' ')
visited[start] = True
for i in range(self.v):
if (Graph.adj[start][i] == 1 and
(not visited[i])):
self.DFS(i, visited)
v, e = 5, 4
G = Graph(v, e)
G.addEdge(0, 1)
G.addEdge(0, 2)
G.addEdge(0, 3)
G.addEdge(0, 4)
visited = [False] * v
G.DFS(0, visited);
|
C#
using System;
using System.Collections.Generic;
class GFG {
static List<List<int>> adj;
static void addEdge(int x, int y)
{
adj[x][y] = 1;
adj[y][x] = 1;
}
static void dfs(int start, List<bool> visited)
{
Console.Write(start + " ");
visited[start] = true;
for (int i = 0; i < adj[start].Count; i++)
{
if (adj[start][i] == 1 && (!visited[i]))
{
dfs(i, visited);
}
}
}
static void Main(string[] args) {
int v = 5;
int e = 4;
adj = new List<List<int>>(v);
for (int i = 0; i < v; i++)
{
adj.Add(new List<int>(v));
for (int j = 0; j < v; j++)
{
adj[i].Add(0);
}
}
addEdge(0, 1);
addEdge(0, 2);
addEdge(0, 3);
addEdge(0, 4);
List<bool> visited = new List<bool>(v);
for (int i = 0; i < v; i++)
{
visited.Add(false);
}
dfs(0, visited);
}
}
|
Javascript
let ans="";
class Graph {
constructor(v, e) {
this.v = v;
this.e = e;
this.adj = Array.from(Array(v), () => new Array(v).fill(0));
}
addEdge(start, end) {
this.adj[start][end] = 1;
this.adj[end][start] = 1;
}
DFS(start, visited) {
ans = ans +start + " ";
visited[start] = true;
for (let i = 0; i < this.v; i++) {
if (this.adj[start][i] === 1 && !visited[i]) {
this.DFS(i, visited);
}
}
}
}
const v = 5;
const e = 4;
const G = new Graph(v, e);
G.addEdge(0, 1);
G.addEdge(0, 2);
G.addEdge(0, 3);
G.addEdge(0, 4);
const visited = new Array(v).fill(false);
G.DFS(0, visited); console.log(ans);
|
The time complexity of the above implementation of DFS on an adjacency matrix is O(V^2), where V is the number of vertices in the graph. This is because for each vertex, we need to iterate through all the other vertices to check if they are adjacent or not.
The space complexity of this implementation is also O(V^2) because we are using an adjacency matrix to represent the graph, which requires V^2 space.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...