If tan 2A = cot (A – 18°), where 2A is an acute angle, then find the value of A
Last Updated :
12 Dec, 2021
Trigonometry is the relation between the angles and sides of a right-angled triangle. In a right angles triangle, there are 3 angles of which one angle is a right angle (90°) and the other two angles are acute angles and there are 3 sides. The side opposite to the right angle is called Hypotenuse. There are 6 ratios between these sides based on the angle between them and they are called Trigonometric Ratios.
The 6 Trigonometric ratios are:
- Sine (sin)
- Cosine (cos)
- Tangent (tan)
- Cosecant (cosec)
- Secant (sec)
- Cotangent (cot)
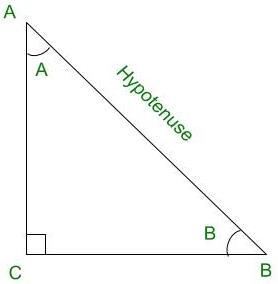
Right angled triangle CBA
Sine (sin):
Sine of an angle is defined by the ratio of lengths of sides which is opposite to the angle and the hypotenuse. For the above triangle, sin A = BC/AB
Cosine (cos):
Cosine of an angle is defined by the ratio of lengths of sides which is adjacent to the angle and the hypotenuse. For the above triangle, cos A = AC/AB
Tangent (tan):
Tangent of an angle is defined by the ratio of the length of sides which is opposite to the angle and the side which is adjacent to the angle. For the above triangle, tan A = BC/AC
Cosecant (cosec):
Cosecant of an angle is defined by the ratio of the length of the hypotenuse and the side opposite the angle. For the above triangle, cosec A = AB/BC
Secant (sec):
Secant of an angle is defined by the ratio of the length of the hypotenuse and the side and the side adjacent to the angle For the above triangle, sec A = AB/AC
Cotangent (cot):
Cotangent of an angle is defined by the ratio of length of sides which is adjacent to the angle and the side which is opposite to the angle. For the above triangle, cot A = AC/BC
If tan 2A = cot (A – 18°), where 2A is an acute angle, then find the value of A
Solution:

Right Angled Triangle XYZ
It is given that,
tan 2A = cot (A- 18°)
⇒ cot (90° – 2A) = cot (A – 18°) ………… ( Since, tan X = cot (90° – X))
Comparing the angles we get,
90° – 2A = A – 18°
⇒ 3A = 108°
⇒ A = 36°
Therefore, the value of A is 36°.
Similar Questions
Question 1: Find the value of X, if sin 2X = cos (X – 18°), Where 2X is an acute angle.
Solution:
It is given that,
sin 2X = cos (X- 18°)
⇒ cos (90° – 2X) = cos (X- 18°) ………… ( Since, sin X = cos (90° – X) )
Comparing the angles we get,
90° – 2X = X- 18°
⇒ 3X = 108°
⇒ X = 36°
Therefore, the value of X is 36°.
Question 2: Find the value of X, if cosec 2X = sec (X – 21°), Where 2X is an acute angle.
Solution:
It is given that,
cosec 2X = sec (X- 21°)
⇒ sec (90° – 2X) = sec (X- 21°) ………… ( Since, cosec X = sec (90° – X) )
Comparing the angles we get,
90° – 2X = X- 21°
⇒ 3X = 111°
⇒ X = 37°
Therefore, the value of X is 36°.
Question 3: Find the value of X, if cos 2X = sin (X- 24°), Where 2X is an acute angle.
Solution:
It is given that,
cos 2X = sin (X- 24°)
⇒ sin (90° – 2X) = sin (X- 24°) ………… ( Since, cos X = sin (90° – X) )
Comparing the angles we get,
90° – 2X = X- 24°
⇒ 3X = 114°
⇒ X = 38°
Therefore, the value of X is 38°.
Question 4: Find the value of X, if sec 2X = cosec (X- 15°), Where 2X is an acute angle.
Solution:
It is given that,
sec 2X = cosec (X- 15°)
⇒ cosec (90° – 2X) = cosec (X- 15°) ………… ( Since, sec X = cosec (90° – X) )
Comparing the angles we get,
90° – 2X = X- 15°
⇒ 3X = 105°
⇒ X = 35°
Therefore, the value of X is 35°.
Question 5: Find the value of X, if cot 2X = tan (X- 18°), Where 2X is an acute angle.
Solution:
It is given that,
cot 2X = tan (X – 18°)
⇒ tan (90° – 2X) = tan (X – 18°) ………… (Since, cot X = tan (90° – X))
Comparing the angles we get,
90° – 2X = X – 18°
⇒ 3X = 108°
⇒ X = 36°
Therefore, the value of X is 36°.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...