Conic sections are curves generated when a plane intersects a right circular cone at different angles. Conic section has the definition in its name, It is a section formed by cutting a Cone. Each type of intersection gives different kinds of curves. Depending upon the angle at which the plane is intersecting, the shape of the curve varies, and forms different curves like Parabola, Hyperbola, Ellipse, etc.

We can obtain the following curves from the intersections:
- Circle
- Parabola
- Hyperbola
- Ellipse
There are certain characteristics that are common to each curve’s equations. Let’s study each of them and see how we can identify them from their equations.
Circle
Circle is set of points which are equidistant from a fixed point.
The figure below represents a circle whose centre is given by O and the radius is the line joining the centre to any point on the circle.

Its equation is given by,
(x – h)2 + (y – k)2 = r2
Where (h, k) is the centre of the circle, and the radius is given by “r”. This equation can be rearranged to bring it in the following form:
x2 + y2 -2hx -2kx + h2 + k2 = r2
Identifying Circles from their Equations
A circle will have both x and y squares present in its equation with non-zero coefficients. Both x2 and y2 must have the same sign. Once we know it’s an equation of the circle, the curve can be recovered.
For Example:
The equation given is, 4x2+ 4y2+ 7y= 9, The easiest way to identify when the given equation is the equation of a circle,
1. Both squares of x and y are present in the equation.
2. The coefficients of the squares of x and y are same (here, +4).
These two information tells that the provided curve’s equation is a Circle.
Parabola
A parabola is the set of all points in a plane that are equidistant from a fixed line and a fixed point (not on the line) in the plane
The fixed-line is called directrix and the point is called the focus.

Standard equations of Parabola
Equation of a standard parabola with x-axis as its axis, passing through the origin and focus at (a,0) is given by,
y2 = 4ax
The figures below show different types of parabolas with their equations.




Identifying Parabola from its equations
To recognize an equation of a parabola from the expanded equation. We need to notice only one thing. The parabola equations should have either y or x squared but not both. The rest of the values can be anything. If an equation has either x or y squared but not both. Then it can be rearranged in the form of a standard equation of a parabola.
For Example:
Take a look at these equations,
x2= y+ 4, y2– 3x+ 9= 0
Both the equations mentioned above are a Parabola because,
1. Both equations have one of the variables squared, but not both. Therefore, the equations are parabola.
Ellipse
An ellipse is a set of all the points in a plane, the sum of whose distances from two fixed points in a plane is constant.
The two points mentioned in the definition above are called foci of the ellipse.

The standard equation of the ellipse that has the x-axis as the major axis and the y-axis as the minor axis is given by,
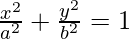
Where, c2 = a2 – b2
In case the ellipse has a major axis on the y-axis and so on. Then the equation is given by,
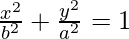

Identifying ellipses from their equation: As similar to circles, ellipses also have x and y squares. But the difference is they will have different coefficients.
For Example:
5x2+ 7y2– 9x- 6y = 0, 9y2+ 2y2+ 8x+ y= 0
Both the equations are the curves of ellipse because,
1. Both x and y variables are squared.
2. The coefficients of both squared variables are different in values (if the coefficients were equal, the curve would be a Circle)
Hyperbola
Hyperbola is a set of points in a plane, the difference of whose distances from two fixed points in the plane is a constant.

The standard equation of Hyperbola is given by,
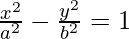
Here also, c2 = a2 – b2
In the above case, the transverse axis is the x-axis, and the conjugate axis is the y-axis. If the axes are reversed, the equation will turn out to be,
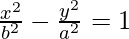
Identifying a hyperbola from its equation: As similar to circles, hyperbolas also have x and y squares. But the difference is they will have different coefficients and the signs will be opposite.
For Example:
5x2– 2y2+ 7x= 8
The above equation is the equation of a Hyperbola since,
1. Both x and y with a degree 2 present.
2. one of the squared variables have different sign than other, in this case y2 coefficient is negative and x2 coefficient is positive.
Let’s see some sample problems on these concepts
Sample Problems
Question 1: Identify the curve from it’s expanded equation.
y2 -4y + 2 = 12x
Solution:
y2 – 4y + 2 = 12x
This equation contains only y square. We have seen in the previous sections that the parabola equations have either x or y squared. So, this must be the equation of the parabola.
Rearranging the given equation,
y2 – 4y + 2 = 12x
⇒ y2 – 4y + 4 + 2 – 4 = 12x
⇒(y – 2)2 – 2 =12x
⇒(y – 2)2 = 12x + 2
⇒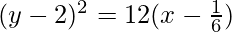
Question 2: Identify the curve from its expanded equation:
4x2 + 9y2 = 36
Solution:
4x2 + 9y2 = 36
The given equation has both x and y squares present in it. Both have positive but different coefficients. So, it might be an equation of ellipse.
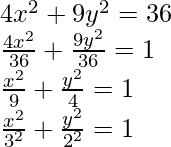
So, this is the equation with a = 3 and b = 2.
Question 3: Identify the curve from its expanded equation:
7x2 – 9y2 = 36
Solution:
7x2 – 9y2 = 36
This equation also has squares of both x and y, but the signs are different. Based on the above-mentioned method, we can say that this is a hyperbola.
Now we need to bring the expanded equation in standard form.
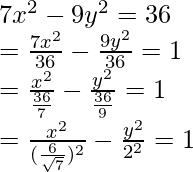
Here, a = 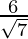 and b = 2
and b = 2
Question 4: Given the expanded equation of a curve, identify it and bring it back to the standard form.
x2 + y2 + 6y = 27
Solution:
x2 + y2 + 6y = 27
Both x and y squares are present and have same sign and 1 as their coefficient. This is an equation of a circle.
x2 + y2 + 6y = 27
⇒ x2 + y2 + 6y + 9 = 27 + 9
⇒ x2 + (y + 3)2 = 36
⇒ x2 + (y + 3)2 = 62
This is the equation of circle with centre at (0,-3) and radius 6.
Question 5: Identify the curve and formulate its equation from the given expression.
x2 + y2 + 4x + 6x = 12
Solution:
Let’s take the given equation,
x2 + y2 + 4x + 6x = 12
From the equations we have studied above, notice that in the given equation x and y both are squared and both have the same sign and same coefficients. As mentioned previously, equations of circle should have both x and y squares with same sign and coefficients. Thus, this is the equation of the circle.
To find the centre and the radius of the circle, we need to rearrange it.
x2 + y2 + 4x + 6x = 12
We need to make whole squares out of the x and y terms
x2 + 4x + y2 + 6x = 12
⇒ x2 + 4x + 4 – 4 + y2 + 6x + 9 – 9 = 12
⇒ (x + 2)2 -4 + (y + 3)2 – 9 = 12
⇒ (x + 2)2 + (y + 3)2 = 12 + 9 + 4
⇒(x + 2)2 + (y + 3)2 = 25
⇒(x + 2)2 + (y + 3)2 = 52
So, the centre is (-2,-3) and the radius is 5.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...