Hypothesis Testing in R Programming
Last Updated :
05 Jul, 2023
A hypothesis is made by the researchers about the data collected for any experiment or data set. A hypothesis is an assumption made by the researchers that are not mandatory true. In simple words, a hypothesis is a decision taken by the researchers based on the data of the population collected. Hypothesis Testing in R Programming is a process of testing the hypothesis made by the researcher or to validate the hypothesis. To perform hypothesis testing, a random sample of data from the population is taken and testing is performed. Based on the results of the testing, the hypothesis is either selected or rejected. This concept is known as Statistical Inference. In this article, we’ll discuss the four-step process of hypothesis testing, One sample T-Testing, Two-sample T-Testing, Directional Hypothesis, one sample 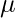 -test, two samples
-test, two samples 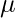 -test and correlation test in R programming.
-test and correlation test in R programming.
Four Step Process of Hypothesis Testing
There are 4 major steps in hypothesis testing:
- State the hypothesis- This step is started by stating null and alternative hypothesis which is presumed as true.
- Formulate an analysis plan and set the criteria for decision- In this step, a significance level of test is set. The significance level is the probability of a false rejection in a hypothesis test.
- Analyze sample data- In this, a test statistic is used to formulate the statistical comparison between the sample mean and the mean of the population or standard deviation of the sample and standard deviation of the population.
- Interpret decision- The value of the test statistic is used to make the decision based on the significance level. For example, if the significance level is set to 0.1 probability, then the sample mean less than 10% will be rejected. Otherwise, the hypothesis is retained to be true.
One Sample T-Testing
One sample T-Testing approach collects a huge amount of data and tests it on random samples. To perform T-Test in R, normally distributed data is required. This test is used to test the mean of the sample with the population. For example, the height of persons living in an area is different or identical to other persons living in other areas.
Syntax: t.test(x, mu) Parameters: x: represents numeric vector of data mu: represents true value of the mean
To know about more optional parameters of t.test(), try the below command:
help("t.test")
Example:
r
x <- rnorm(100)
t.test(x, mu = 5)
|
Output:
One Sample t-test
data: x
t = -49.504, df = 99, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 5
95 percent confidence interval:
-0.1910645 0.2090349
sample estimates:
mean of x
0.008985172
- Data: The dataset ‘x’ was used for the test.
- The determined t-value is -49.504.
- Degrees of Freedom (df): The t-test has 99 degrees of freedom.
- The p-value is 2.2e-16, which indicates that there is substantial evidence refuting the null hypothesis.
- Alternative hypothesis: The true mean is not equal to five, according to the alternative hypothesis.
- 95 percent confidence interval: (-0.1910645, 0.2090349) is the confidence interval’s value. This range denotes the values that, with 95% confidence, correspond to the genuine population mean.
Two Sample T-Testing
In two sample T-Testing, the sample vectors are compared. If var. equal = TRUE, the test assumes that the variances of both the samples are equal.
Syntax: t.test(x, y) Parameters: x and y: Numeric vectors
Example:
r
x <- rnorm(100)
y <- rnorm(100)
t.test(x, y)
|
Output:
Welch Two Sample t-test
data: x and y
t = -1.0601, df = 197.86, p-value = 0.2904
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.4362140 0.1311918
sample estimates:
mean of x mean of y
-0.05075633 0.10175478
Directional Hypothesis
Using the directional hypothesis, the direction of the hypothesis can be specified like, if the user wants to know the sample mean is lower or greater than another mean sample of the data.
Syntax: t.test(x, mu, alternative) Parameters: x: represents numeric vector data mu: represents mean against which sample data has to be tested alternative: sets the alternative hypothesis
Example:
r
x <- rnorm(100)
t.test(x, mu = 2, alternative = 'greater')
|
Output:
One Sample t-test
data: x
t = -20.708, df = 99, p-value = 1
alternative hypothesis: true mean is greater than 2
95 percent confidence interval:
-0.2307534 Inf
sample estimates:
mean of x
-0.0651628
One Sample 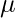 -Test
-Test
This type of test is used when comparison has to be computed on one sample and the data is non-parametric. It is performed using wilcox.test() function in R programming.
Syntax: wilcox.test(x, y, exact = NULL) Parameters: x and y: represents numeric vector exact: represents logical value which indicates whether p-value be computed
To know about more optional parameters of wilcox.test(), use below command:
help("wilcox.test")
Example:
r
x <- rnorm(100)
wilcox.test(x, exact = FALSE)
|
Output:
Wilcoxon signed rank test with continuity correction
data: x
V = 2555, p-value = 0.9192
alternative hypothesis: true location is not equal to 0
- Data: The dataset ‘x’ was used for the test.
- The calculated test statistic or V value is 2555.
- P-value: The null hypothesis is weakly supported by the p-value of 0.9192.
- The alternative hypothesis asserts that the real location is not equal to 0. This indicates that there is a reasonable suspicion that the distribution’s median or location parameter is different from 0.
Two Sample 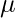 -Test
-Test
This test is performed to compare two samples of data. Example:
r
x <- rnorm(100)
y <- rnorm(100)
wilcox.test(x, y)
|
Output:
Wilcoxon rank sum test with continuity correction
data: x and y
W = 5300, p-value = 0.4643
alternative hypothesis: true location shift is not equal to 0
Correlation Test
This test is used to compare the correlation of the two vectors provided in the function call or to test for the association between the paired samples.
Syntax: cor.test(x, y) Parameters: x and y: represents numeric data vectors
To know about more optional parameters in cor.test() function, use below command:
help("cor.test")
Example:
r
cor.test(mtcars$mpg, mtcars$hp)
|
Output:
Pearson's product-moment correlation
data: mtcars$mpg and mtcars$hp
t = -6.7424, df = 30, p-value = 1.788e-07
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.8852686 -0.5860994
sample estimates:
cor
-0.7761684- Data: The variables’mtcars$mpg’ and’mtcars$hp’ from the ‘mtcars’ dataset were subjected to a correlation test.
- t-value: The t-value that was determined is -6.7424.
- Degrees of Freedom (df): The test has 30 degrees of freedom.
- The p-value is 1.788e-07, indicating that there is substantial evidence that rules out the null hypothesis.
- The alternative hypothesis asserts that the true correlation is not equal to 0, indicating that “mtcars$mpg” and “mtcars$hp” are significantly correlated.
- 95 percent confidence interval: (-0.8852686, -0.5860994) is the confidence interval. This range denotes the values that, with a 95% level of confidence, represent the genuine population correlation coefficient.
- Correlation coefficient sample estimate: The correlation coefficient sample estimate is -0.7761684.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...