Hyperparameters Optimization methods – ML
Last Updated :
12 Dec, 2023
In this article, we will discuss the various hyperparameter optimization techniques and their major drawback in the field of machine learning.
What are the Hyperparameters?
Hyperparameters are those parameters that we set for training. Hyperparameters have major impacts on accuracy and efficiency while training the model. Therefore it needed to be set accurately to get better and efficient results. Let’s discuss some Hyperparameters Optimization Methods to optimize the hyperparameter.
Hyperparameters Optimization Technique
Exhaustive Search Methods
Let’s first discuss some Exhaustive Search Methods to optimize the hyperparameter.
- Grid Search: In Grid Search, the possible values of hyperparameters are defined in the set. Then these sets of possible values of hyperparameters are combined by using Cartesian product and form a multidimensional grid. Then we try all the parameters in the grid and select the hyperparameter setting with the best result.
- Random Search: This is another variant of Grid Search in which instead of trying all the points in the grid we try random points. This solves a couple of problems that are in Grid Search such as we don’t need to expand our search space exponentially every time add a new hyperparameter
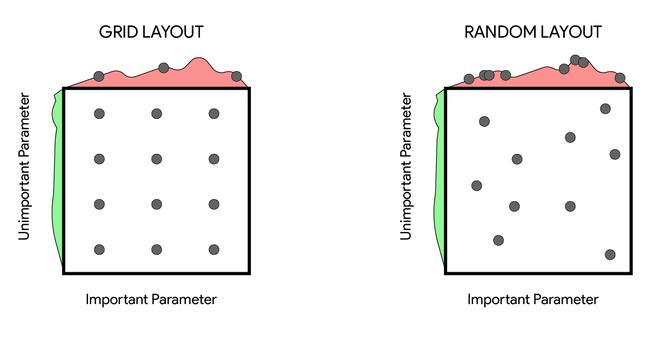
Drawback:
Random Search and Grid Search are easy to implement and can run in parallel but here are few drawbacks of these algorithm:
- If the hyperparameter search space is large, it takes a lot of time and computational power to optimize the hyperparameter.
- There is no guarantee that these algorithms find local maxima if the sample is not meticulously done.
Bayesian Optimization:
Instead of random guess, In bayesian optimization we use our previous knowledge to guess the hyper parameter. They use these results to form a probabilistic model mapping hyperparameters to a probability function of a score on the objective function. These probability function is defined below.

This function is also called “surrogate” of objective function. It is much easier to optimize than Objective function. Below are the steps for applying Bayesian Optimization for hyperparameter optimization:
- Build a surrogate probability model of the objective function
- Find the hyperparameters that perform best on the surrogate
- Apply these hyperparameters to the original objective function
- Update the surrogate model by using the new results
- Repeat steps 2–4 until n number of iteration
Sequential Model-Based Optimization:
Sequential Model-Based Optimization (SMBO) is a method of applying Bayesian optimization. Here sequential refers to running trials one after another, each time improving hyperparameters by applying Bayesian probability model (surrogate).
There are 5 important parameters of SMBO:
- Domain of the hyperparameter over which .
- An objective function which outputs a score which we want to optimize.
- A surrogate distribution of objective function
- A selection function to select which hyperparameter to choose next. Generally we take Expected Improvement into the consideration
- A data structure contains history of previous (score, hyperparmeter) pairs which are used in previous iterations.
There are many different version SMBO hyperparameter optimization algorithm. These common difference between them is the surrogate functions. Some surrogate function such as Gaussian Process, Random Forest Regression, Tree Prazen Estimator. In this post we will discuss Tree Prazen Estimator below.
Tree Prazen Estimators:
Tree Prazen Estimators uses tree-structure for optimizing the hyperparameter. Many hyperprameter can be optimized by using this method such as number of layers, optimizer in the model, number of neurons in each layer. In tree prazen estimator instead of calculating  we calculate
we calculate  and P(y) (where y is an intermediate score that decides how good this hyperparameter values such as validation loss and x is hyperparameter).
and P(y) (where y is an intermediate score that decides how good this hyperparameter values such as validation loss and x is hyperparameter).
In first of Tree Prazen Estimator, we sample the validation loss by random search in order to initialize the algorithm. Then we divide the observations into two groups: the best performing one (e.g. the upper quartile) and the rest, taking y* as the splitting value for the two groups.
Then we calculate the probability of hyperparameter being in each of these groups such as
 = f(x) if y<y* and
= f(x) if y<y* and  = g(x) if y>y*.
= g(x) if y>y*.
The two densities and g are modelled using Parzen estimators (also known as kernel density estimators) which are a simple average of kernels centred on existing data points.
P(y) is calculated using the fact that p(y<y*)= f(y*) which defines the percentile split in the two categories.
Using Baye’s rule (i.e. p(x, y) = p(y)  ), it can be shown ) that the definition of expected improvements equivalent to f(x)/g(x).
), it can be shown ) that the definition of expected improvements equivalent to f(x)/g(x).
In this final step we try to maximize the \frac{f(x)}{g(x)}
Drawback:
The biggest disadvantage of Tree Prazen Estimator that it selects hyperparameter independently of each other, that somehow effects the efficiency and computation required because in most of the neural networks there are relationships between different hperparameters
Other Hyperparameter Estimation Algorithms:
Hyperband:
The underlying principle of this algorithm is that if a hyperparameter configuration is destined to be the best after a large number of iterations, it is more likely to perform in the top half of configurations after a small number of iterations. Below is step-by-step implementation of Hyperband.
- Randomly sample n number of hyperparameter sets in the search space.
- After k iterations evaluate the validation loss of these hyperpameters.
- Discard the half of lowest performing hyperparameters .
- Run the good ones for k iterations more and evaluate and discard the bottom half.
- Repeat until we have only one model of hyperparameter left.
Drawbacks:
If number of samples is large some good performing hyperparameter sets which required some time to converge may be discarded early in the optimization.
Population based Training (PBT):
Population based Training (PBT) starts similar to random based training by training many models in parallel. But rather than the networks training independently, it uses information from the remainder of the population to refine the hyperparameters and direct computational resources to models which show promise. This takes its inspiration from genetic algorithms where each member of the population, referred to as a worker, can exploit information from the rest of the population. for instance, a worker might copy the model parameters from a far better performing worker. It also can explore new hyperparameters by changing the present values randomly.
Bayesian Optimization and HyperBand (BOHB):
BOHB (Bayesian Optimization and HyperBand) is a combination of the Hyperband algorithm and Bayesian optimization. First, it uses Hyperband capability to sample many configurations with a small budget to explore quickly and efficiently the hyper-parameter search space and get very soon promising configurations, then it uses the Bayesian optimizer predictive capability to propose set of hyperparameters that are close to optimum.This algorithm can also be run in parallel (as Hyperband) which overcomes a strong drawback of Bayesian optimization.
Frequently Asked Questions (FAQs)
Q. 1 What are hyperparameters in machine learning?
Hyperparameters are pre-established parameters that are not learned during the training process. They control a machine learning model’s general behaviour, including its architecture, regularisation strengths, and learning rates.
Q.2 What is Hyperparameter optimization(HPO)?
The process of determining the ideal set of hyperparameters for a machine learning model is known as hyperparameter optimization. Usually, strategies like grid search, random search, and more sophisticated ones like genetic algorithms or Bayesian optimization are used to accomplish this.
Q. 3 What is Grid Search?
Grid search is a method that thoroughly examines a manually-specified portion of the targeted algorithm’s hyperparameter space. In contrast, random search uses a probability distribution to independently choose a value for every hyperparameter.
Q. 4 How does cross-validation play a role in hyperparameter optimization?
In hyperparameter optimization, cross-validation is essential because it yields a more reliable estimate of model performance. The process entails dividing the dataset into several folds, training the model on various subsets, and assessing the model’s effectiveness using the remaining data.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...